Bayesovské Statistiky vysvětlil Začátečníky v Jednoduché angličtině

Přehled

• nevýhody frequentist statistiky vedou k potřebě Bayesovské Statistiky
• Zjistit, Bayesovská Statistika a bayesovy věty
• Existují různé metody k testování významnosti modelu, jako je p-value, interval spolehlivosti, atd.

Úvod

Bayesovské Statistiky nadále zůstávají nepochopitelné, v podnítil myslích mnoha analytiků., Být ohromen neuvěřitelnou silou strojového učení, mnoho z nás se stalo nevěrným statistikám. Naše zaměření se zúžilo na zkoumání strojového učení. Není to pravda?

nechápeme, že strojové učení není jediným způsobem, jak vyřešit problémy reálného světa. V několika situacích nám to nepomůže řešit obchodní problémy, i když se na těchto problémech podílejí data. Přinejmenším znalost statistik vám umožní pracovat na složitých analytických problémech bez ohledu na velikost dat.,

v 1770s, Thomas Bayes představil ‚Bayesova věta‘. Ani po staletích význam „Bayesovské statistiky“nezmizel. Ve skutečnosti se dnes toto téma vyučuje ve velkých hloubkách na některých předních světových univerzitách.

s touto myšlenkou jsem vytvořil průvodce pro začátečníky o Bayesovské statistice. Snažil jsem se zjednodušeně vysvětlit pojmy s příklady. Předchozí znalost základní pravděpodobnosti& statistika je žádoucí., Měli byste se podívat na tento kurz, abyste získali komplexní minimum statistik a pravděpodobnosti.

na konci tohoto článku budete mít konkrétní pochopení Bayesovské statistiky a jejích souvisejících konceptů.,>Bayesův Teorém

Bayesian Závěr

• Bernoulliho funkce pravděpodobnosti
• Předchozí Přesvědčení, Distribuce
• Zadní přesvědčení, Distribuce

Test na Významu – Frequentist vs Bayesovské

• p-hodnota
• interval Spolehlivosti
• Bayes Faktor
• Vysoká Hustota Interval (HDI)

předtím, Než jsme se ponořit do Bayesovské Statistiky, dejte nám strávit pár minut chápání Frequentist Statistik, více populární verze statistik, většina z nás narazit a vlastní problémy.,

Frequentist Statistiky

debata mezi frequentist a bayesovské straší začátečníky po staletí. Proto je důležité pochopit rozdíl mezi těmito dvěma a jak existuje tenká linie vymezení!

Jedná se o nejpoužívanější inferenční techniku ve statistickém světě. Infact, obecně je to první myšlenková škola, na kterou se člověk vstupující do světa statistik setkává.

Frequentist Statistics testuje, zda událost (hypotéza) nastane nebo ne., Vypočítá pravděpodobnost události v dlouhodobém horizontu experimentu (tj. experiment se opakuje za stejných podmínek, aby se získal výsledek).

zde se odebírají vzorkovací distribuce pevné velikosti. Pak se experiment teoreticky opakuje nekonečně mnohokrát, ale prakticky se provádí se zastavovacím záměrem. Například provádím experiment s zastavovacím záměrem na mysli, že pokus zastavím, když se opakuje 1000krát nebo vidím minimálně 300 hlav v hodu mincí.

pojďme teď hlouběji.,

nyní pochopíme statistiky frequentist pomocí příkladu hodu mincí. Cílem je odhadnout spravedlnost mince. Níže je tabulka představující frekvenci z hlavy:

víme, že pravděpodobnost, že hlavu na vyhazování spravedlivé mince je 0,5. No. of heads představuje skutečný počet získaných hlav. Difference je rozdíl mezi 0.5*(No. of tosses) - no. of heads.,

důležité je si uvědomit, že, i když rozdíl mezi skutečným počtem hlav a očekává, že počet hlav( 50% počet hodů), zvyšuje se počet hodů zvyšuje se podíl počet kusů na celkový počet hodů přístupy 0.5 (pro spravedlivou minci).

Tento experiment nám předkládá velmi častou chybu našel v frequentist přístup, tj. Závislost výsledek experimentu na počet, kolikrát se experiment opakovat.,

Chcete-li se dozvědět více o častých statistických metodách, můžete se vydat na tento vynikající kurz inferenciálních statistik.

inherentní nedostatky ve statistice Frequentist

až Zde jsme viděli jen jednu chybu ve statistikách frequentist. No, je to jen začátek.

20. století viděl masivní vzestup v frequentist statistiky uplatňuje numerické modely, třeba zjistit, zda vzorek je odlišný od ostatních, parametr je dost důležité, aby se držel v modelu a variousother projevy testování hypotéz., Časté statistiky však utrpěly některé velké nedostatky ve svém designu a interpretaci, které představovaly vážné obavy ve všech skutečných životních problémech. Například:

p-values měřen vzorek (pevná velikost) statistika s některými zastavení záměr změny změny v záměru a velikosti vzorku. tj. pokud dvě osoby pracují na stejných datech a mají jiný záměr zastavení, mohou získat dvě různé p- values pro stejná data, což je nežádoucí.,

například: osoba a se může rozhodnout přestat házet minci, když celkový počet dosáhne 100, zatímco B se zastaví na 1000. U různých velikostí vzorků získáváme různé T-skóre a různé p-hodnoty. Podobně se záměr zastavit může změnit z pevného počtu převrácení na celkovou dobu převrácení. I v tomto případě jsme povinni získat různé hodnoty p.

2 – interval spolehlivosti (C.i) jakop-value silně závisí na velikosti vzorku., To činí zastavovací potenciál naprosto absurdním, protože bez ohledu na to, kolik osob provádí testy na stejných datech, výsledky by měly být konzistentní.

3 – Intervaly Spolehlivosti (C. I) není rozdělení pravděpodobnosti a proto neposkytují nejpravděpodobnější hodnotu pro parametr a nejpravděpodobnější hodnoty.

tyto tři důvody stačí k tomu, abyste přemýšleli o nevýhodách frekventistického přístupu a proč existuje potřeba bayesovského přístupu. Pojďme to zjistit.,

odtud nejprve pochopíme základy Bayesovské statistiky.

Bayesovská Statistika

„Bayesovská statistika je matematický postup, který aplikuje pravděpodobnosti na statistické problémy. Poskytuje lidem nástroje k aktualizaci jejich přesvědčení v důkazech o nových datech.“

máš to? Dovolte mi to vysvětlit příkladem:

Předpokládejme, že ze všech 4 mistrovských závodů (F1) mezi Niki Laudou a Jamesem Huntem Niki vyhrál 3krát, zatímco James zvládl pouze 1.,

takže pokud byste vsadili na vítěze dalšího závodu, kdo by byl ?

vsadím se, že byste řekl Niki Lauda.

zde je twist. Co když vám bude řečeno, že jednou pršelo, když James vyhrál a jednou, když Niki vyhrál, a je jisté, že příští den bude pršet. Na koho byste teď vsadil své peníze ?

intuicí je snadné vidět, že šance na výhru pro Jamese se drasticky zvýšily. Ale otázka zní: kolik ?,

pochopit problém po ruce, musíme se seznámit s některými pojmy, z nichž první je podmíněná pravděpodobnost (vysvětleno níže).

kromě toho, tam jsou určité předpoklady:

Předpoklady:

1. Lineární Algebra : Chcete osvěžit základy, můžete se podívat na Khan Academy Algebry.
2. pravděpodobnost a základní statistiky: Chcete-li obnovit své základy, můžete se podívat na další kurz Khan Academy.

3.,1 Podmíněné Pravděpodobnosti

je definována jako: Pravděpodobnost, že událost nastane dané „B“, se rovná pravděpodobnosti “ B „a děje spolu děleno pravděpodobnost B“.

Pro příklad: Předpokládejme, že dva částečně protínajících se množin a a B, jak je znázorněno níže.

Set a představuje jednu sadu událostí a Set B představuje jinou. Chceme vypočítat pravděpodobnost, že daná B se již stala. Umožňuje reprezentovat dění události B zastíněním červeně.,

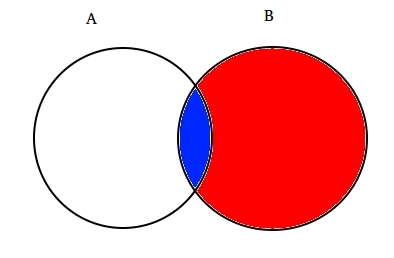
Teď, když B se stalo, že část, která teď záleží na je část zabalená v modré barvě, který je zajímavé je . Takže, pravděpodobnosti A za předpokladu B, se ukázalo být:

Proto můžeme napsat vzorec pro událost B dána již došlo:

nebo

a Teď druhá rovnice může být přepsána jako :

Toto je známé jako Podmíněná Pravděpodobnost.,

pokusme se odpovědět na sázkový problém s touto technikou.

Předpokládejme, že B je událost vítězství Jamese Hunta. A být událost prší. Proto,

Dosazení hodnot v podmíněná pravděpodobnost vzorec, dostaneme pravděpodobnost kolem 50%, což je téměř dvojnásobek 25%, když déšť nebyl brán v úvahu (Řešení je na svém konci).

to dále posílilo naši víru, že James vyhrál ve světle nových důkazů, tj., Musíte se divit, že tento vzorec se podobá něčemu, o čem jste možná hodně slyšeli. Mysli!

pravděpodobně jste to uhodli správně. Vypadá to jako Bayesova věta.

Bayesova věta je postavena na podmíněné pravděpodobnosti a leží v srdci Bayesovské Inference. Pojďme to pochopit podrobně.

3.2 Bayesova Věta

Bayesova Věta vstoupí v platnost, když více událostí vytvořit vyčerpávající soubor s jinou akci B. To by mohlo být chápáno s pomocí níže uvedené schéma.,

B lze zapsat jako

Takže pravděpodobnost, že B lze zapsat jako,

Tak, nahrazení P(B) do rovnice podmíněné pravděpodobnosti dostaneme

Tohle je rovnice Bayesova Věta.

Bayesovská Inference

nemá smysl se ponořit do teoretického aspektu. Takže se dozvíme, jak to funguje!, Vezměme si příklad házení mincí, abychom pochopili myšlenku Bayesovské inference.

důležitou součástí Bayesovské inference je stanovení parametrů a modelů.

modely jsou matematickou formulací pozorovaných událostí. Parametry jsou faktory v modelech ovlivňujících pozorovaná data. Například při házení mince může být spravedlnost mince definována jako parametr mince označený θ. Výsledek událostí může být označen d.

odpovězte na to nyní., Jaká je pravděpodobnost 4 hlav z 9 hodů (D) vzhledem k férovosti mince (θ). jsem.e P(D|θ)

Počkejte, udělal jsem správně ptát? Č.

měli Bychom být více zajímat : Vzhledem k výsledku (D) jaká je probbaility mince fér (θ=0.5)

Umožňuje reprezentovat pomocí Bayesova Věta:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

Zde P(θ) je před já.e sílu naší víry ve spravedlnost mince před tím, než hodit., Je naprosto v pořádku věřit, že mince může mít jakýkoli stupeň spravedlnosti mezi 0 a 1.

P(D|θ) je pravděpodobnost pozorování našeho výsledku vzhledem k naší distribuci pro θ. Pokud bychom věděli, že mince byla spravedlivá, dává to Pravděpodobnost pozorování počtu hlav v určitém počtu Salta.

P(D) je důkazem. Toto je pravděpodobnost dat, jak je určena součtem (nebo integrací) napříč všemi možnými hodnotami θ, váženými podle toho, jak silně věříme v tyto konkrétní hodnoty θ.,

Pokud bychom měli více pohledů na to, co spravedlnost mince je (ale to nevěděl jistě), pak to nám říká, že pravděpodobnost, že určité sekvence hodů pro všechny možnosti naší víry v minci je spravedlnost.

P(θ|D) je zadní víra našich parametrů po pozorování důkazů, tj. počet hlav .

odtud se ponoříme hlouběji do matematických důsledků tohoto konceptu. Neboj se. Jakmile je pochopíte, dostat se k jeho matematice je docela snadné.,

abychom správně definovali náš model, potřebujeme před rukou dva matematické modely. Jeden reprezentuje funkci pravděpodobnosti P (D / θ) a druhý pro reprezentaci rozdělení předchozích přesvědčení . Produkt těchto dvou dává distribuci zadní víry P (θ|D).

protože předchozí a zadní jsou obě víry o rozdělení spravedlnosti mince, intuice nám říká, že oba by měli mít stejnou matematickou podobu. Mějte to na paměti. Vrátíme se k tomu znovu.,

existuje tedy několik funkcí, které podporují existenci bayesovy věty. Znát je důležité, proto jsem je podrobně vysvětlil.

4.1. Funkce pravděpodobnosti Bernoulli

umožňuje shrnout, co jsme se dozvěděli o funkci pravděpodobnosti. Takže jsme se dozvěděli, že:

je to Pravděpodobnost pozorování určitého počtu hlav v určitém počtu Salta pro danou spravedlnost mince. To znamená, že naše pravděpodobnost pozorování hlav / ocasů závisí na spravedlnosti mince (θ).,

P(y=1|θ)=

P(y=0|θ)=

za povšimnutí stojí, že představuje 1 jako hlavy a 0 jako orel, je jen matematický zápis formulovat model. Výše uvedené matematické definice můžeme kombinovat do jediné definice, abychom reprezentovali pravděpodobnost obou výsledků.

P(y|θ)=

Toto se nazývá Bernoulliho Funkce Pravděpodobnosti a úkolem mince obracející se nazývá Bernoulliho pokusů.,

y={0,1},θ=(0,1)

A když chceme vidět řadu rubů, nebo převrátí, jeho pravděpodobnost je dán vztahem:

Kromě toho, pokud nás zajímá pravděpodobnost, že počet hlav z objevoval v N počet hodů, pak pravděpodobnost je dán vztahem:

4.2. Předchozí distribuce víry

tato distribuce se používá k reprezentaci našich silných stránek na přesvědčení o parametrech založených na předchozí zkušenosti.,

ale co když člověk nemá žádné předchozí zkušenosti?

nebojte se. Matematici vymysleli metody, jak tento problém zmírnit. To je známé jako uninformative priors. Rád bych vás předem informoval, že je to jen nesprávné pojmenování. Každý neinformativní prior vždy poskytuje nějakou Informační událost konstantní distribuce před.

matematická funkce používaná k reprezentaci předchozích přesvědčení je známá jakobeta distribution., Má některé velmi pěkné matematické vlastnosti, které nám umožňují modelovat naše přesvědčení o binomické distribuci.

funkce hustoty pravděpodobnosti beta distribuce má tvar :

kde se zaměřujeme na čitatele. Jmenovatel je tam jen proto, aby se zajistilo, že celková hustota pravděpodobnosti funkce při integraci vyhodnocuje na 1.

α β se nazývá tvar rozhodování parametrů funkce hustoty., α je analogický počet hlav ve studiích a β odpovídá počtu ocasů., Níže uvedené diagramy vám pomohou vizualizovat beta rozdělení pro různé hodnoty α β

i Vy můžete čerpat beta rozdělení pro sebe pomocí následující kód v R:

Poznámka: α β jsou intuitivní, aby pochopili, protože mohou být vypočteny na základě znalosti střední hodnoty (μ) a směrodatná odchylka (σ) rozdělení., Ve skutečnosti, oni jsou příbuzní jako :

Pokud se průměr a standardní odchylku distribuce jsou známé , pak je tvar parametrů lze snadno vypočítat.

Závěr vyvodit z grafů výše:

1. Když tam byl žádný přehazovat jsme věřili, že každý spravedlnosti mince je možné, jak je znázorněno na rovnou linii.
2. když bylo více hlav než ocasů, graf ukázal vrchol posunutý směrem k pravé straně, což naznačuje vyšší pravděpodobnost hlav a tato mince není spravedlivá.,
3. jak se provádí více hodů, a hlavy stále přicházejí ve větším poměru vrchol zužuje zvýšení naší důvěry v spravedlnost hodnoty mince.

4. 3. Distribuce zadní víry

důvodem, proč jsme si vybrali předchozí přesvědčení, je získání beta distribuce. Je to proto, že když ji vynásobíme funkcí pravděpodobnosti, zadní distribuce získá formu podobnou předchozí distribuci, která je mnohem snazší se vztahovat a pochopit., Pokud tolik informací povzbudí vaši chuť k jídlu, jsem si jistý, že jste připraveni jít další míli.

pojďme vypočítat zadní víru pomocí bayesovy věty.

Výpočet zadní přesvědčení pomocí Bayesova Věta

Nyní, naše zadní víra se stává,

Tohle je zajímavé., Stačí znát průměr a standardní distribuce našich přesvědčení o parametr θ a tím, že sleduje počet líců v N hodech, můžeme aktualizovat naše přesvědčení o model parametr(θ).

umožňuje pochopit pomocí jednoduchého příkladu:

Předpokládejme, že si myslíte, že mince je zkreslená. Má střední (μ) zaujatost kolem 0,6 se standardní odchylkou 0,1.

α= 13.8 β=9.2

.,E naše distribuce bude zaujatá na pravé straně. Předpokládejme, že jste pozorovali 80 hlav (z=80) ve 100 saltech(N=100). Pojďme se podívat, jak naše prior a posterior přesvědčení budou vypadat:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

Umožňuje vizualizovat jak názory na grafu:

R kód pro výše uvedený graf je jako:

}

Jak více a více vyletí a nová data je pozorován, naše přesvědčení se dostanou aktualizovány., To je skutečná síla Bayesovské Inference.

Test na Významu – Frequentist vs Bayesovské

Aniž by se do přísné matematické struktury, tento oddíl vám poskytne rychlý přehled o různých přístupech frequentist a bayesovské metody zkoušení pro význam a rozdíl mezi skupinami a která metoda je nejspolehlivější.

5.1. p-hodnota

v tomto se vypočítá t-skóre pro konkrétní vzorek z distribuce vzorkování pevné velikosti. Pak se předpovídají hodnoty p., Můžeme interpretovat hodnoty p jako (příklad hodnoty p jako 0,02 pro rozdělení průměrných 100) : existuje 2% pravděpodobnost, že vzorek bude mít průměr rovný 100.

tato interpretace trpí vadou, že pro vzorkování distribucí různých velikostí je člověk povinen získat různé T-skóre a tím i jinou p-hodnotu. Je to naprosto absurdní. Hodnota p menší než 5% nezaručuje, že nulová hypotéza je špatná, ani hodnota p větší než 5% zajišťuje, že nulová hypotéza je správná.

5.2., Intervaly spolehlivosti

intervaly spolehlivosti také trpí stejnou vadou. Navíc, protože c. i není rozdělení pravděpodobnosti, neexistuje způsob, jak zjistit, které hodnoty jsou nejpravděpodobnější.

5.3. Bayesův faktor

Bayesův faktor je ekvivalentem hodnoty p v bayesovském rámci. Umožňuje pochopit to komplexním způsobem.

nulovou hypotézu ve bayesovský rámec předpokládá, ∞ rozdělení pravděpodobnosti pouze na konkrétní hodnotu parametru (řekněme θ=0.5) a nulovou pravděpodobnost, že jinde, kde., (M1)

alternativní hypotéza je, že všechny hodnoty θ jsou možné, tedy plochá křivka představuje rozdělení. (M2)

nyní vypadá zadní distribuce nových dat níže.

Bayesovská statistika upravila důvěryhodnost (pravděpodobnost) různých hodnot θ. Lze snadno vidět, že rozdělení pravděpodobnosti se posunulo směrem k M2 s hodnotou vyšší než M1 i.e m2 je pravděpodobnější.,

Bayesův faktor nezávisí na skutečných distribučních hodnotách θ, ale na velikosti posunu hodnot M1 a M2.

v panelu a( je uvedeno výše): levý pruh (M1) je předchozí pravděpodobnost nulové hypotézy.

v panelu B (zobrazeno) je levý pruh zadní pravděpodobností nulové hypotézy.

Bayesův faktor je definován jako poměr zadní šance na předchozí kurzy,

odmítnout nulovou hypotézu, a BF <1/10 má přednost.,

můžeme vidět okamžité výhody použití Bayesova faktoru namísto p-hodnot, protože jsou nezávislé na záměrech a velikosti vzorku.

5.4. Interval vysoké hustoty (HDI)

HDI je vytvořen ze zadní distribuce po pozorování nových dat. Vzhledem k tomu, HDI je pravděpodobnost, 95% HDI dává 95% nejvíce důvěryhodné hodnoty. Je také zaručeno, že hodnoty 95% budou v tomto intervalu ležet na rozdíl od oznámení C.i.

, jak je 95% HDI v předchozí distribuci širší než 95% zadní distribuce., Je to proto, že naše víra v HDI se zvyšuje při pozorování nových dat.

Poznámky

cílem tohoto článku bylo, aby si myslíte o jiný typ statistické filozofie venku a jak jeden z nich nelze použít v každé situaci.

je nejvyšší čas, aby se obě filozofie spojily, aby zmírnily problémy skutečného světa tím, že řeší nedostatky druhého., Část II této série se zaměří na techniky redukce dimenzionality pomocí algoritmů MCMC (Markovův řetězec Monte Carlo). Část III bude na základě vytvoření Bayesovská regrese model od nuly a interpretaci jeho výsledků v R. Takže předtím, než začnu s Částí II, chtěl bych mít vaše návrhy / zpětnou vazbu na tento článek.