|
„Bi“ znamená „dva“ (jako bicykl má dvě kola) … |
 |

Házení Mincí:
- získali jsme Hlavy (H) nebo
- Orel (T)
Můžeme říct, že pravděpodobnost, že mince přistání H je ½
A pravděpodobnost, že mince je přistávací T je ½
Pojďme Hodit Mincí!
hodit spravedlivou minci třikrát … jaká je šance získat dvě hlavy?,tr>












Which outcomes do we want?,
“ dvě hlavy „mohou být v libovolném pořadí:“ HHT“,“ THH „a“ HTH “ mají všechny dvě hlavy (a jeden ocas).
takže 3 výsledků produkují „dvě hlavy“.
jaká je pravděpodobnost každého výsledku?,podniky jsou (P znamená „Pravděpodobnost“):
- P(Tři Hlavy) = P(HHH) = 1/8
- P(Dvě Hlavy) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Jedna Hlava) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Nula Hlavy) = P(TTT) = 1/8
můžeme napsat, že to z hlediska Náhodnou Proměnnou, X, = „počet Hlav od 3 hodí mincí“:
- P(X = 3) = 1/8
- P(X = 2) = 3/8
- P(X = 1) = 3/8
- P(X = 0) = 1/8
A to je, jak to vypadá ve formě grafu:
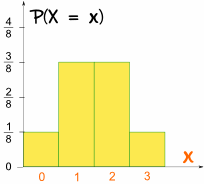
je To symetrické!,
Tvorba Vzorce
Teď si představte, že chceme, aby pravděpodobnost 5 hlav v 9 hodí: seznam všech 512 výsledků bude trvat dlouhou dobu!
takže uděláme vzorec.
v našem předchozím příkladu, jak můžeme získat hodnoty 1, 3, 3 a 1 ?
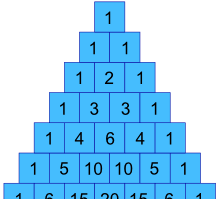
No, jsou vlastně v Pascalově trojúhelníku !
můžeme je vyrobit pomocí vzorce?
Jistě, že můžeme, a tady to je:
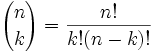
To je často nazýváno „n nad k“.
- n = celkový počet
- k = počet chceme
- „!,“znamená “ faktoriál“, například 4! = 1×2×3×4 = 24
můžete si o tom přečíst více na kombinacích a permutacích.
zkusme to:
použijeme to pro těžší otázku:
zaujatost!
šance na úspěch nebo neúspěch byly dosud stejně pravděpodobné.
ale co když jsou mince zkreslené (přistát více na jedné straně než na druhé) nebo volby nejsou 50/50.
příklad: prodáváte sendviče. 70% lidí si vybere kuře, zbytek si vybere něco jiného.
to je stejně jako příklad hlav a ocasů, ale s 70/30 místo 50/50.,
nakreslíme stromový diagram:
jsou zvýrazněny případy“ dvou kuřat“.
pravděpodobnosti pro „dvě kuřata“ jsou 0,147, protože v každém případě vynásobíme dva 0,7 s a jeden 0,3. Jinými slovy
0.147 = 0.7 × 0.7 × 0.3
Nebo pomocí mocniny:
= 0.72 x 0.31
0,7, je pravděpodobnost každého výběru chceme, říkat p
2, je počet možností chceme, říkat k
A máme (zatím):
= pk × 0.31
0.,3 je pravděpodobnost opačně, tak to je: 1−p
1 je číslo opačné volby, tak to je: n−k
Což nám dává:
= pk(1-p)(n-k)
, Kde
- p je pravděpodobnost, že každá volba, kterou chceme,
- k je počet možností, chceme
- n je celkový počet možností,
Nyní víme, že pravděpodobnost každého výsledku je 0.147
na tlačítko OK. To bylo hodně práce pro něco, co jsme už věděli, ale teď máme vzorec, který můžeme použít pro těžší otázky.,
dát dohromady
nyní víme, jak vypočítat, kolik:
n!k!(n-k)!
a pravděpodobnost každého:
pk(1-p) (n-k)
když se násobí dohromady, dostaneme:
Pravděpodobnost k Z n způsoby:
P (K Z n) = n!k!(n-k)! pk(1-p)(n-k)
Obecné rozdělení Binomické Vzorce,
Důležité upozornění:
- pokusy jsou nezávislé,
- Existují pouze dva možné výsledky v každé studii,
- pravděpodobnost „úspěchu“ v každém pokusu je konstantní.,
Quincunx

Mají hrát s Quincunx (pak si přečtěte Quincunx Vysvětlil), aby vidět Binomické Rozdělení v akci.
Hodit kostkou
spravedlivý smrt je hozen čtyřikrát. Výpočet pravděpodobnosti získání:
- 0 Dvojky
- 1
- 2 Dvojky
- 3 Dvojky
- 4 Dvojky
V tomto případě n=4, p = P(Dvě) = 1/6
X je Náhodná Proměnná ‚Počet Dvou ze čtyř hody‘.,
náhradní x = 0 až 4 do vzorce:
P ( K Z n) = n!k!(n-k)! pk(1-p) (n-k)
takto (na 4 desetinná místa):
tentokrát graf není symetrický:
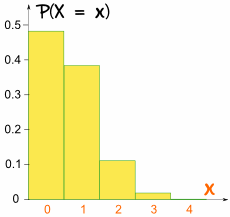
není symetrický!
To je zkreslený, protože p není 0.5

Sportovní Kola
Vaše společnost dělá sportovní kola. 90% projít závěrečnou kontrolu (a 10% selhání a je třeba opravit).
jaký je očekávaný průměr a rozptyl 4 dalších inspekcí?
nejprve vypočteme všechny pravděpodobnosti.,
- n = 4,
- p = p (Pass) = 0,9
X je náhodná proměnná „počet průchodů ze čtyř kontrol“.
náhradní x = 0 až 4 do vzorce:
P ( K Z n) = n!k!(n-k)! PK(1-p) (n-k)
Střední, rozptyl a směrodatná odchylka
pojďme vypočítat průměr, rozptyl a směrodatnou odchylku pro kontroly sportovních kol.
pro ně existují (relativně) jednoduché vzorce. Jsou trochu těžké dokázat,ale pracují!,
průměr, nebo „očekávaná hodnota“, je:
μ = np
vzorec pro Rozptyl je:
Rozptyl: σ2 = np(1-p)
A Směrodatná Odchylka je odmocnina z rozptylu:
σ = √(np(1-p))
Pro sportovní kola:
Rozptyl: σ2 = 4 × 0.9 × 0.1 = 0.36
Směrodatná Odchylka je:
σ = √(0.36) = 0,6.


Napsat komentář