Calc zdroj

Teoretické pozadí

obsah

Úvod

konzolový paprsek je jednou z nejjednodušších struktur. Má pouze jednu podporu, na jednom z jejích konců. Podpora je takzvaná pevná podpora, která brání veškerému pohybu, včetně vertikálních nebo horizontálních posunů a jakýchkoli rotací. Druhý konec není podporován, a proto se může volně pohybovat nebo otáčet. Tento volný konec se často nazývá špička konzoly.,

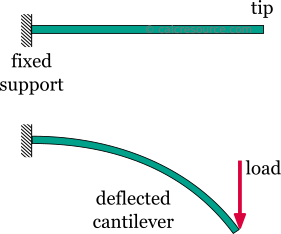
Odstranění připálit podporu, nebo vložením vnitřní závěs, by znamenal, že konzolový nosník do mechanismu: tělo se pohybuje bez omezení v jednom nebo více směrech. To je nežádoucí situace pro nosnou konstrukci. V důsledku toho konzolový paprsek nenabízí žádnou redundanci, pokud jde o podpěry. Pokud dojde k lokálnímu selhání, celá struktura se zhroutí., Tyto typy struktur, které nenabízejí žádnou redundanci, se nazývají kritické nebo determinantní struktury. Naopak struktura, která má více podpěr, než je požadováno pro omezení jeho volných pohybů, se nazývá redundantní nebo neurčitá struktura. Konzolový paprsek je determinantní struktura.

Předpoklady

statická analýza zatížení nosnou konstrukcí zahrnuje odhad jeho vnitřní síly a momenty, stejně jako jeho výchylek., Typicky, na rovině struktury, se v rovině zatížení, vnitřní akce zájmu jsou axiální síla N , příčná smyková síla V a ohybový moment M . U konzolového nosníku, který nese pouze příčné zatížení, je axiální síla vždy nulová, pokud jsou průhyby malé. Proto je spíše běžné zanedbávat axiální síly.,

vypočtené výsledky na této stránce jsou založeny na následujících předpokladech:

• materiál je homogenní a izotropní (jinými slovy, jeho vlastnosti jsou stejné ve stále bod a směrem libovolném směru)
• materiál je lineární, elastický
• zatížení ve statické způsobem (nemění se s časem)
• průřez je stejný po celé délce nosníku
• průhyby jsou malé
• Každý průřez že zpočátku je letadlo a také kolmo k podélné ose, zůstává v rovině a kolmo na osy vychýlen příliš., To je případ, kdy je výška průřezu poměrně menší než délka nosníku (10krát nebo více) a také průřez není vícevrstvý (nikoli sendvičový Typ).

poslední dva předpoklady splňují kinematické požadavky na teorii paprsku Euler Bernoulli, která je zde také přijata.

sign convention

pro výpočet vnitřních sil a momentů je při každém řezu paprsku nutná sign convention., Zde jsou přijata následující:

1. axiální síla je považována za pozitivní, když způsobuje napětí části
2. smyková síla je pozitivní, když způsobuje hodinovou rotaci součásti.
3. ohybový moment je pozitivní, když způsobuje napětí na spodní vlákno paprsku a stlačení na horní vlákno.

tato pravidla, i když nejsou povinná, jsou spíše univerzální. Jiný soubor pravidel, pokud bude důsledně dodržován, by také přinesl stejné fyzické výsledky.,e, V a ohybový moment M

Symboly

• E : materiál modul pružnosti (youngův modul pružnosti)
• já : moment setrvačnosti průřezu kolem elastický neutrální osy ohybu
• L : celková délka nosníku
• R : podpora reakce
• d : výchylek
• M : ohybový moment
• V : příčné smykové síly
• \theta : sklon

Konzolový nosník s jednotným distribuovaný náklad

zatížení w je distribuován po celém konzolové span, má konstantní velikost a směr., Jeho rozměry jsou síla na délku. Celkové množství síly aplikované na konzolový paprsek je W=w L, kde L délka paprsku. V závislosti na okolnostech může být dána buď celková síla W, nebo rozložená síla na délku w.

následující tabulka obsahuje vzorce, které popisují statické reakce konzolový nosník pod jednotným distribuovaný náklad w .

Konzolový nosník s bodem síly na špičce

síla je soustředěna v jednom bodě, který se nachází na volném konci nosníku., V praxi však může být síla rozložena na malé ploše, i když rozměry této oblasti by měla být podstatně menší než konzolový délky. V těsné blízkosti aplikace síly se očekávají koncentrace stresu a v důsledku toho je reakce předpovídaná klasickou teorií paprsku možná nepřesná. Jedná se však pouze o místní jev. Když se vzdalujeme od místa síly, výsledky se stanou platnými na základě principu Saint-Venant.,

následující tabulka obsahuje vzorce popisující statickou odezvu konzolového paprsku pod koncentrovanou bodovou silou P, uloženou na špičce.

konzolový paprsek s bodovou silou v náhodné poloze

síla je soustředěna v jediném bodě, kdekoli po délce konzoly. V praxi však může být síla rozložena na malé ploše. Aby se však síla považovala za koncentrovanou, měly by být rozměry aplikační oblasti podstatně menší než délka nosníku., V těsné blízkosti síly se očekávají koncentrace napětí a v důsledku toho reakce předpovídaná klasickou teorií paprsku možná nepřesná. Jedná se však pouze o místní jev, a když se vzdalujeme od místa síly, rozpor výsledků se stává zanedbatelným.

následující tabulka obsahuje vzorce, které popisují statické reakce konzolový nosník pod koncentrovanou sílu P , uložené v náhodné vzdálenosti od pevné podpory.,

konzolový paprsek s bodovým momentem

v tomto případě je okamžik uložen v jediném bodě paprsku, kdekoli přes rozpětí. Z praktického hlediska by to mohl být silový pár nebo člen v kroucení, spojený z roviny a kolmý na paprsek.

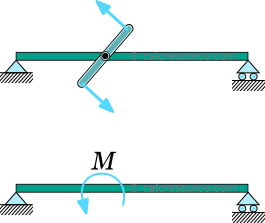
V každém případě, v okamžiku, kdy aplikační oblasti by se rozšířila do malé délce konzolové, takže to může být úspěšně idealizovaný jako koncentrovaný moment k bodu., I když v těsné blízkosti oblasti použití, předpokládané výsledky, a to prostřednictvím klasického paprsku teorie se očekává, že budou nepřesné (z důvodu koncentrace napětí a další lokalizované účinky), předpokládané výsledky se stanou dokonale platné, když jsme se vzdálit, jak je uvedeno v Saint-Venant principu.

následující tabulka obsahuje vzorce, které popisují statické reakce konzolový nosník pod koncentrovaného bodu moment M , uložené v určité vzdálenosti od pevné podpory.,

Konzolový nosník s různou rozložené zatížení

zatížení je distribuován po celém konzolový délky, s lineárně různé velikosti, od w_1 na pevnou podporu, w_2 na volném konci. Rozměry w_1 a w_2 jsou síla na délku. Celkové množství síly aplikované na paprsek je W={L \ over2} (w_1 + w_2), kde L Délka konzoly.

následující tabulka obsahuje vzorce popisující statickou odezvu konzolového paprsku při různém rozloženém zatížení lichoběžníkového tvaru.,

Konzolový nosník s deskou-typ lichoběžníkové rozložení zatížení

Toto rozložení je typické pro konzolové nosníky nosné desky. Rozdělení vypadá jako lichoběžník, s rostoucí část v blízkosti pevnou podporu a konstantní část, s velikostí rovná w , na zbývající délce, až ke špičce. Rozměry w jsou síla na délku. Celkové množství síly působící na nosníku je W=w (L-a/2) , kde L je konzolový délky a, a , je délka blízkosti pevnou podporu, kde rozložení zatížení je různé (trojúhelníkové).,

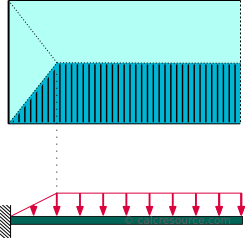
následující tabulka obsahuje vzorce, které popisují statické reakce konzolový nosník pod lichoběžníkové rozložení zatížení, vzhledem k desce, jak je znázorněno ve schématu výše.

Konzolový nosník s částečně distribuované rovnoměrné zatížení

zatížení je distribuován na část samonosné délky, s konstantní velikosti w , zatímco zbývající délka je uvolněn. Rozměry w jsou síla na délku., Celkové množství síly aplikované na paprsek je W=W \ vlevo (L-A-B\vpravo), kde L Délka konzoly a A, b nezatížené délky na levé a pravé straně nosníku.

následující tabulka obsahuje vzorce, které popisují statické reakce konzolový nosník pod částečně distribuované rovnoměrné zatížení.

Konzolový nosník s částečně distribuované lichoběžníkové zatížení

zatížení je distribuován na část samonosné délky, s lineárně různé velikosti od w_1 na w_2 , zatímco zbývající délka je uvolněn., Rozměry w_1 a w_2 jsou síla na délku. Celkové množství síly aplikované na paprsek je W = {L-A-B \ over2} (w_1 + w_2), kde L délka paprsku A A, b nezatížené délky na levé a pravé straně nosníku.

následující tabulka obsahuje vzorce popisující statickou odezvu konzolového paprsku pod částečně rozloženým lichoběžníkovým zatížením.,