|
Dva trojúhelníky jsou shodné, pokud mají:
ale nemusíme znát všechny tři strany a všechny tři úhly …obvykle stačí tři ze šesti. |
Existuje pět způsobů, jak zjistit, zda dva trojúhelníky jsou shodné: SSS, SAS, ASA, AAS a HL.,
SSS (side, side, side)
SSS znamená „side, side, side“ a znamená, že máme dva trojúhelníky se všemi třemi stranami rovnými.
například:
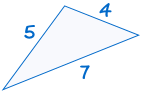 |
je shodný s: | 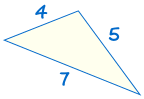 |
(Viz Řešení Trojúhelníků SSS zjistit více).
Pokud tři strany jednoho trojúhelníku se rovná tři strany, trojúhelník, trojúhelníky jsou shodné.,
SAS (strana, úhel, strana)
SAS je zkratka pro „strana, úhel, strana“ a znamená to, že máme dva trojúhelníky, kde známe dvě strany a úhel náklonu jsou stejné.,
například:
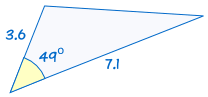 |
je shodný s: | 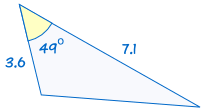 |
(Viz Řešení SAS Trojúhelníky zjistit více).
Pokud se dvě strany a úhel náklonu jednoho trojúhelníku se rovná odpovídající si strany a úhel, trojúhelník, trojúhelníky jsou shodné.,
ASA (úhel, strana, úhel)
ASA je zkratka pro „úhel, strana, úhel“ a znamená to, že máme dva trojúhelníky, kde víme, že dva úhly a zahrnuty strana jsou stejné.,
například:
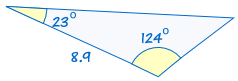 |
je shodný s: | 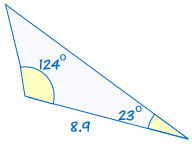 |
(Viz Řešení ASA Trojúhelníky zjistit více).
Pokud jsou dva úhly a součástí strany jednoho trojúhelníku jsou stejné odpovídající si úhly a boční trojúhelník, trojúhelníky jsou shodné.,
AAS (úhel, úhel, strana)
AAS je zkratka pro „úhel, úhel, strana“ a znamená to, že máme dva trojúhelníky, kde víme, že dva úhly a non-zahrnuty strana jsou stejné.,
například:
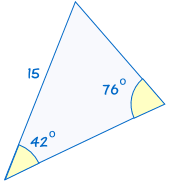 |
je shodný s: | 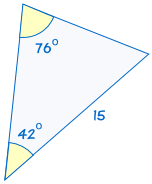 |
(Viz Řešení AAS Trojúhelníky zjistit více).
Pokud jsou dva úhly, a non-součástí strany jednoho trojúhelníku jsou stejné odpovídající si úhly a boční trojúhelník, trojúhelníky jsou shodné.
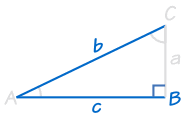
HL (hypotenze, noha)
toto platí pouze pro pravoúhlé trojúhelníky!,
 |
nebo | 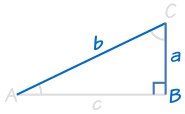 |
HL je zkratka pro „Přepona, Noha“ (nejdelší strana pravoúhlého trojúhelníka se nazývá „přepona“, další dvě strany jsou tzv. „nohy“)
To znamená, že máme dva pravoúhlé trojúhelníky,
- stejnou délku přepony a
- stejnou délku pro jeden z dalších dvou nohách.
nezáleží na tom, která noha, protože trojúhelníky lze otáčet.,
například:
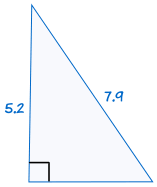 |
je shodný s: | 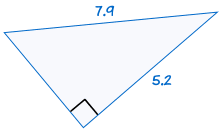 |
(Viz pythagorovy Věty zjistit více).
Pokud přeponu a jednu nohu z jednoho pravoúhlého trojúhelníku se rovná odpovídající přepony a úseku další pravoúhlý trojúhelník, dva trojúhelníky jsou shodné.
pozor! Nepoužívejte “ AAA “
AAA znamená, že máme všechny tři úhly trojúhelníku, ale žádné strany.,
toto není dostatek informací k rozhodnutí, zda jsou dva trojúhelníky shodné!
Protože trojúhelníky mohou mít stejné úhly, ale být různé velikosti:
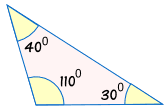 |
není shodný s: | 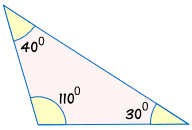 |
Aniž by věděl, alespoň na jedné straně, nemůžeme být jisti, zda dva trojúhelníky jsou shodné.





Napsat komentář