Molekulární Kinetické Teorie Plynů

Tlak a KMT

makroskopické jevy tlaku mohou být vysvětleny z hlediska molekulární kinetické teorie plynů. Předpokládejme případ, kdy je molekula plynu (reprezentovaná sférou) v krabici, délka L (Obrázek 1). Pomocí předpoklady stanovené výše, a vzhledem k tomu, koule se pohybuje pouze v x-směru, můžeme zkoumat například z oblasti kolize elasticky s jednou ze stěn krabice.,

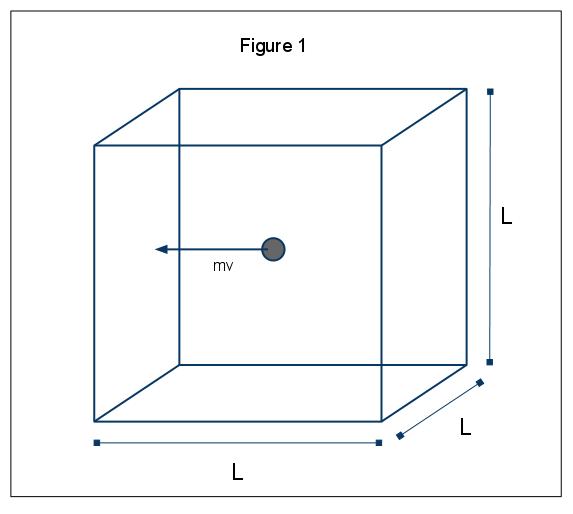
hybnost této kolize je dána vztahem p=mv, v tomto případě p=mvx, protože jsme pouze s ohledem na x rozměr. Celková změna hybnosti za tuto kolizi je pak dána tím,

\

Vzhledem k tomu, že množství času to bere mezi srážky molekul se stěnou je L/vx můžeme dát frekvenci srážek molekul proti dané stěny krabice za jednotku času, jako vx/2L., Nyní lze vyřešit změnu hybnosti za jednotku času:

\

řešení pro hybnost za jednotku času dává sílu vyvíjenou objektem (F=ma=p/čas)., S výrazem, že F=mvx2/L lze nyní vyřešit pro tlak vyvíjený molekulární kolize, kde oblast je uvedena jako oblast jedné stěně krabice, A=L2:

\

\

výraz, mohou být zapsány, pokud jde o tlak spojený s kolizí od N počet molekul:

\

Tento výraz může nyní být upravena tak, aby účet pro pohyb v osách x, y a z směrech pomocí mean-square velocity pro tři rozměry a velké hodnoty N., Výraz je nyní napsán jako:

\

tento výraz nyní dává tlak, makroskopickou kvalitu, pokud jde o atomový pohyb. Význam výše uvedeného vztahu spočívá v tom, že tlak je úměrný střední čtvercové rychlosti molekul v dané nádobě. Proto, jak se zvyšuje molekulární rychlost, tak i tlak vyvíjený na nádobu.