V této lekci, budeme postavit pět (5) běžné logické spojky nebo operátorů. Jsou považovány za běžné logické konektivity, protože jsou velmi populární, užitečné a vždy se učí společně.
než začneme, navrhuji, abyste si prohlédli mou další lekci, ve které je odkaz uveden níže.
Tento úvodní lekci o pravdivostní tabulky obsahuje předpoklad znalosti nebo informace, které vám pomohou lépe pochopit obsah této lekce.,
Úvod do Pravdivostní Tabulky, Výkazy a Spojky
Le je začít tím, že výpis pěti (5) běžné logické spojky.
Pět (5) Běžné Logické Spojky nebo Subjekty
- Logické Negace
- Logické Spojení (A)
- Logické Disjunkce (Včetně OR)
- Logické Implikace (Podmíněné)
- Logické Biconditional (Dvojité Implikace)
I., Pravdivostní Tabulka Logické Negace
negace prohlášení je také prohlášení s pravdivostní hodnotu, která je přesně opačný, že z původní prohlášení. Například negací tvrzení je napsán symbolicky jako
~\large{P} nebo \large{\neg P}.
~{P} nebo {\neg P} je číst jako „P.“
Pamatujte si: operátor negace označuje symbolem ~ nebo \neg má pravdu hodnoty původní prohlášení, pak výstup přesný opak jeho pravdivostní hodnotu., Jinými slovy, negace jednoduše zvrátí hodnotu pravdy daného prohlášení. Pokud je tedy tvrzení P pravdivé, pak je pravdivá hodnota jeho negace falešná. Stejným způsobem, je-li p nepravdivé, je pravdivá hodnota jeho negace.

II. Pravdivostní Tabulka Logické Spojení
spojení je typ složený příkaz, který se skládá ze dvou propozic (také známé jako jednoduché prohlášení) spojeny operátorem AND.,
symbol, který se používá k reprezentaci A nebo logické spojení subjektu je \color{red}\Large{\wedge}. To vypadá jako obrácené písmeno V.
Pokud máme dva jednoduché výroky P a Q, a chceme tvořit složený příkaz spojeny operátorem AND, můžeme to zapsat jako:
\large{P \wedge Q}.
{P \wedge Q} je číst jako „P a Q“
Pamatujte si: pravdivostní hodnota složeného prohlášení P \wedge Q je pravda, pokud to pravda hodnot P a Q jsou oba pravdivé., V opačném případě je P \ wedge Q falešný.
v následující tabulce pravdy si všimněte, že když je P pravdivý a Q je pravdivý, P \wedge Q je pravdivý. Ostatní tři kombinace výroků P A Q jsou však nepravdivé.

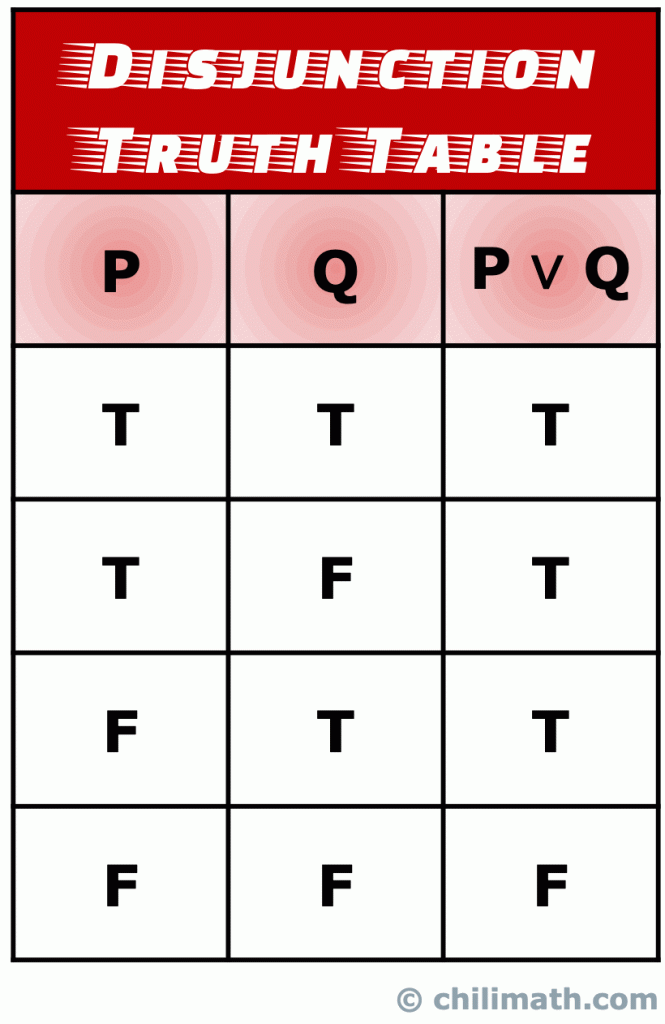
III. Pravdivostní Tabulka Logické Disjunkce
disjunkce je druh složený příkaz, který se skládá ze dvou jednoduchých výroků, který vznikl spojením prohlášení s NEBO provozovatele.
v příkazu disjunction je použití nebo je včetně. To znamená „jeden nebo druhý“ nebo obojí.,
symbol, který se používá k reprezentaci nebo nebo logického operátora disjunkce, je \ color{red} \ Large {\vee }. Připomíná písmeno V abecedy.
Dva výroky P a Q připojil NEBO provozovatel tvořit složený příkaz je napsán jako:
\large{P \vee Q}.
{P \vee Q} je číst jako „P nebo Q“
Pamatujte si: pravdivostní hodnota složeného prohlášení P \vee Q je pravda, pokud pravdivostní hodnota buď dva jednoduché výroky P a Q je pravdivý., Moreso, P \vee Q je také pravda, když pravda hodnoty obou tvrzení P A Q jsou pravdivé. Jediný čas, kdy je příkaz disjunction P \vee Q nepravdivý, se stane, když jsou pravdivé hodnoty P I Q nepravdivé.
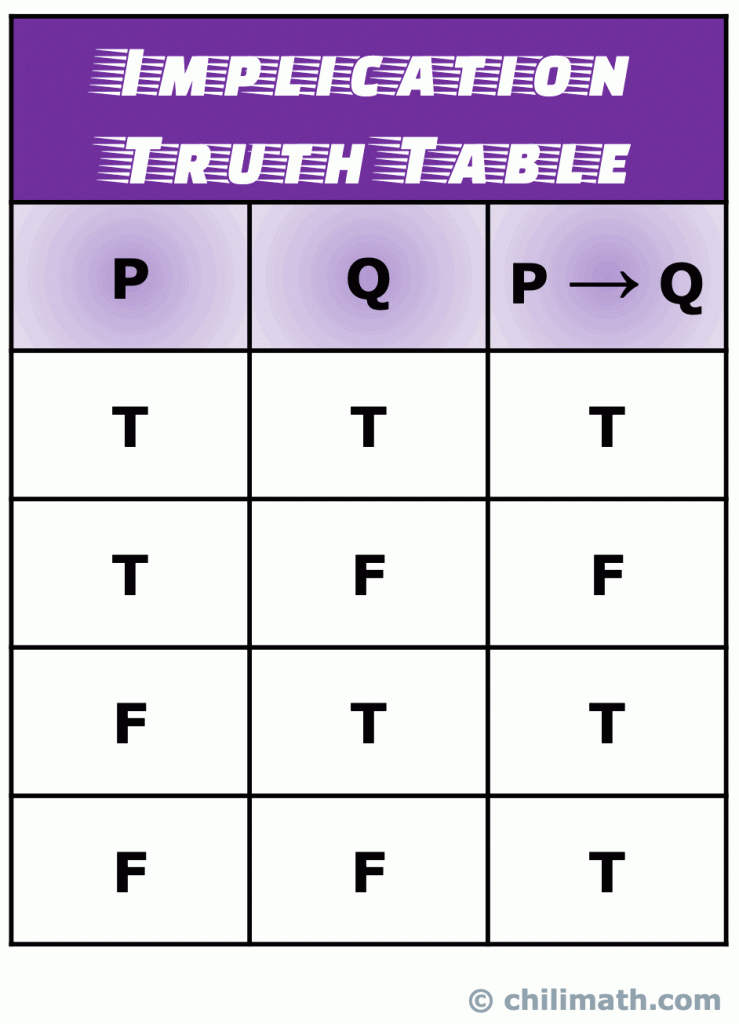
IV. Pravdivostní Tabulka Logické Důsledky
důsledky (také známý jako podmíněné výkazu) typ složený příkaz, který je tvořen spojením dvou jednoduchých výroků s logickými důsledky pojivové nebo provozovatele.,
symbol, který se používá k reprezentaci logického implikačního operátora, je šipka směřující doprava, tedy šipka doprava.

Když se dva jednoduché výroky P a Q jsou spojeny důsledky operátora, máme:
\Large{P \Q}.
- kde P je známá jako hypotéza
- kde Q je známý jako závěr
Existuje mnoho způsobů, jak číst podmíněné {P \Q}., Níže jsou uvedeny některé z mála běžných.
pamatujte: hodnota pravdy složeného příkazu P \to Q je pravdivá, pokud jsou pravdivé jak jednoduché příkazy P, tak Q. Moreso, P \na Q je vždy pravda, pokud P je nepravdivé. Jediný scénář, že P \na Q je false se stane, když P je pravda, a Q je false.
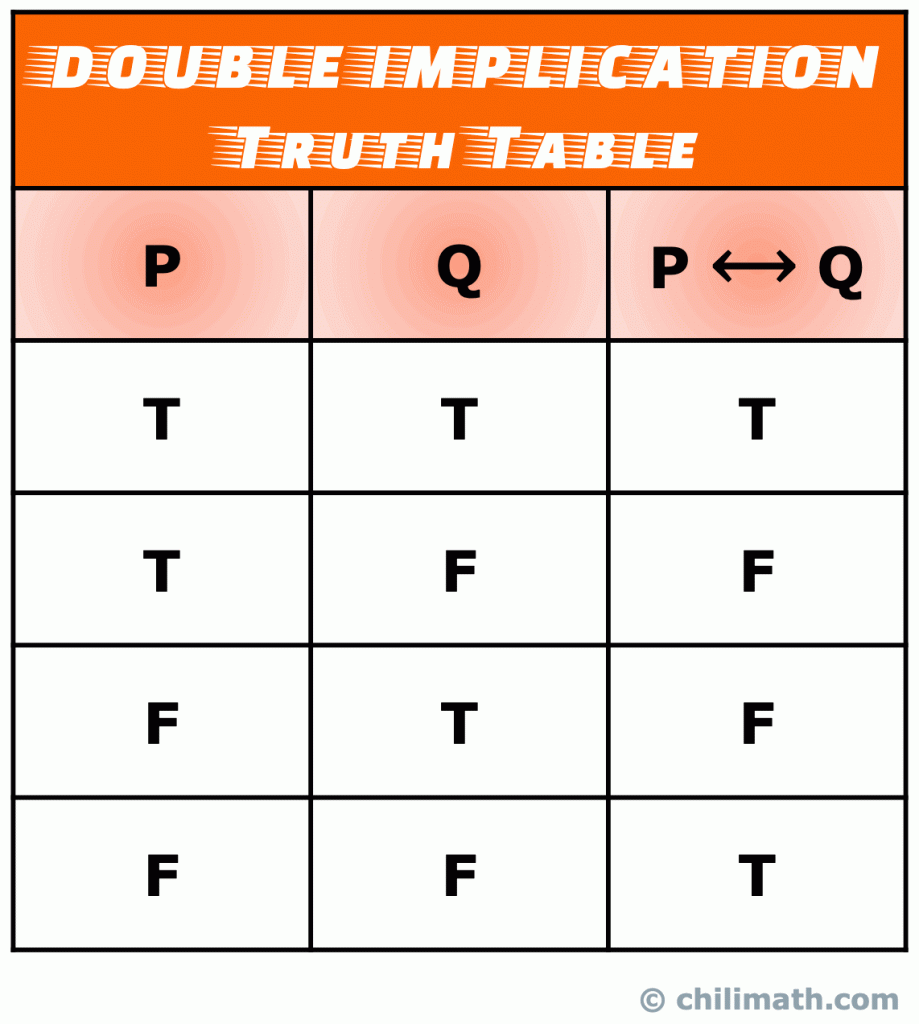
V., Pravdivostní Tabulka Logické Biconditional nebo Dvojité Implikace
dvojité implikace (také známý jako biconditional prohlášení) je typ složený příkaz, který je tvořen spojením dvou jednoduchých výroků s biconditional operátora. Bikondiční prohlášení je opravdu kombinací podmíněného prohlášení a jeho konverzace.
bikondiční operátor je označen dvouhlavou šipkou.,

Když se připojíte dva jednoduché příkazy (také známý jako molekulární prohlášení) s biconditional operátor, dostaneme:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} je číst jako „P tehdy a jen tehdy, když Q.,“
- kde P je známý jako antecedent
- kde Q je známý jako následné
Pamatujte si: pravdivostní hodnota biconditional prohlášení P \leftrightarrow Q je pravdivá, když oba jednoduché výroky P a Q jsou oba pravdivé nebo oba nepravdivé. V opačném případě je P \ leftrightarrow Q false.
mohlo by Vás také zajímat:
Úvod do Pravdivostní Tabulky, Výroky a Logické Spojky
Konverzovat, Inverzní, a Contrapositive o Podmíněný příkaz
Napsat komentář