Jeden z nejznámějších matematických vzorců je Pythagorova Věta, která nám poskytuje vztah mezi stranami v pravoúhlém trojúhelníku. Pravý trojúhelník se skládá ze dvou nohou a hypotenze. Obě nohy se setkávají v úhlu 90° a hypotenze je nejdelší stranou pravého trojúhelníku a je stranou naproti pravému úhlu.,
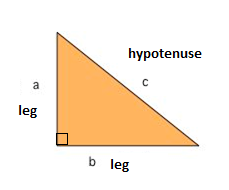
Pythagorova Věta nám říká, že vztah v každém pravoúhlém trojúhelníku je:
$$a^{2}+b^{2}=c^{2}$$
Příklad:
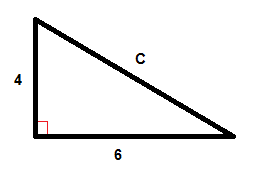
$$C^{2}=6^{2}+4^{2}$$
$$C^{2}=36+16$$
$$C^{2}=52$$
$$C=\sqrt{52}$$
$$C\cca 7.2$$
Existuje několik speciálních typů pravoúhlé trojúhelníky, stejně jako 45°-45° pravoúhlé trojúhelníky a 30°-60° pravoúhlý trojúhelník.,
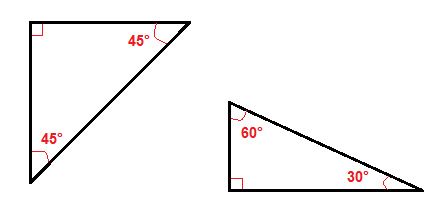
Protože jejich úhlů je snazší najít přepony nebo nohy v těchto pravoúhlé trojúhelníky, než ve všech ostatních pravoúhlé trojúhelníky.
v pravoúhlém trojúhelníku 45°-45° potřebujeme znásobit pouze jednu nohu √2, abychom získali délku hypotenze.
Příklad:
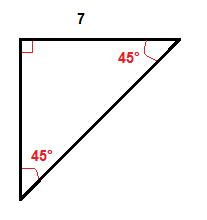
vynásobte délku nohy, která je 7 palců √2, aby si délku přepony.
$7\cdot \ sqrt{2}\cca. 9.,9$$
V 30°-60° pravoúhlý trojúhelník, můžeme najít délku nohy, která je naproti úhlu 30° pomocí tohoto vzorce:
$$a=\frac{1}{2}\cdot c$$
Příklad:
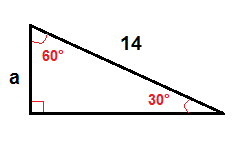
najít, použijeme výše uvedený vzorec.
$$a= \ frac{1}{2} \ cdot 14$
$$a=7$$
video lekce
Najděte strany tohoto pravého trojúhelníku
Napsat komentář