REKLAMY:
znalost pojmu rozpočtové linie nebo co se také nazývá rozpočtové omezení je zásadní pro pochopení teorie spotřebitele rovnováhy.
vyšší křivka lhostejnosti vykazuje vyšší úroveň spokojenosti než nižší. Proto se spotřebitel ve snaze maximalizovat svou spokojenost pokusí dosáhnout nejvyšší možné křivky lhostejnosti.,
ale ve snaze nakupovat stále více zboží a získat tak stále větší spokojenost musí pracovat pod dvěma omezeními: za prvé musí platit ceny za zboží a za druhé má omezený příjem peněz, s nímž může zboží koupit. Jak daleko by tedy za své nákupy šel, závisí na cenách zboží a peněžních příjmech, které musí za zboží utratit.,
REKLAMY:
s cílem vysvětlit spotřebitele je rovnováha, tam je také potřeba pro zavedení do lhostejnost křivky analýzy rozpočtové linie, která představuje ceny zboží a spotřebitel je peněžní příjem.
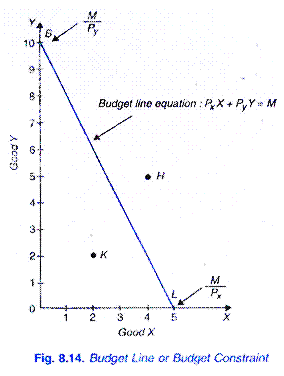
Předpokládejme, že náš spotřebitel má příjem Rs. 50 utratit za dva zboží X a Y. nechte cenu dobrého X na trhu být Rs. 10 na jednotku a Y Rs. 5 na jednotku. Pokud spotřebitel utratí celý svůj příjem Rs. 50 na dobré X, koupil by 5 jednotek X; pokud utratí celý svůj příjem Rs., 50 na dobré Y by si koupil 10 jednotek y. pokud přímka spojující 5xand 10vis nakreslené, dostaneme to, co se nazývá cenová čára nebo rozpočtová čára.
rozpočtová linie tedy ukazuje všechny kombinace dvou zboží, které si spotřebitel může koupit tím, že utratí svůj daný peněžní příjem za dva zboží za dané ceny. Pohled na obr. 8.14 ukazuje, že s Rs. 50 a ceny X a Y jsou Rs 10 a Rs. 5 respektive spotřebitel může koupit l0Y a vůl, nebo stojan IX; nebo 6Y a 2X, nebo 4y a 3X atd.,
REKLAMY:
jinými slovy, může si koupit jakoukoli kombinaci, která leží na rozpočtové linii s jeho dané peníze příjmu a daných cenách statků. Je třeba pečlivě poznamenat, že jakákoliv kombinace dvou zboží, jako jsou H (5Y a 4X), které leží nad a mimo daný rozpočet linka bude mimo dosah spotřebitele.
ale jakákoli kombinace ležící v rozpočtové linii, jako je k (2X a 2y), bude v dosahu spotřebitele, ale pokud si koupí takovou kombinaci, nebude utrácet veškerý svůj příjem Rs. 50., S předpokladem, že celý daný příjem je vynaložen na dané zboží a za dané ceny, si tedy spotřebitel musí vybrat ze všech kombinací, které leží na rozpočtové linii.
shora je zřejmé, že rozpočtová linie graficky ukazuje rozpočtové omezení. Kombinace komodit ležících napravo od rozpočtové linie jsou nedosažitelné, protože příjem spotřebitele nestačí k nákupu těchto kombinací., Vzhledem k tomu, spotřebitelské příjmy a ceny dvou statků, kombinace zboží, ležící nalevo od linie rozpočtu jsou dosažitelné, to znamená, že spotřebitel může koupit některý z nich.
je také důležité si uvědomit, že zachycovací OB na ose Y na obr. 8.14 se rovná výši jeho celého příjmu (M) děleného cenou (PY) komodity Y.to znamená OB = M/PY. Stejně tak intercept OL na ose X měří celkový příjem dělený cenou komodity X. tedy OL = M / Px.,
REKLAMY:
rozpočet řádek lze zapsat algebraicky takto:

Kde Px a Py označují ceny zboží X a Y v tomto pořadí a M je zkratka pro peníze příjmů:
výše rozpočtu-line rovnice (1) vyplývá, že, vzhledem k tomu, peníze, příjem spotřebitele a ceny dvou statků, každá kombinace ležet na rozpočtovou linii bude stát stejné množství peněz, a proto mohou být zakoupeny u uvedených příjmů., Rozpočtová položka může být definována jako množina kombinací dvou komodit, které lze zakoupit v případě celého daného příjmu se vynakládá na ně a její sklon je roven negativní poměr cena.
Cenově Prostor:
To by mělo být pečlivě zřejmé, že rozpočet rovnice PxX + PyY= M a Y = M/Py – Px/PyX líčil rozpočtové linie na Obr. 8.14 popisuje pouze rozpočtovou linii a nikoli rozpočtový prostor., Rozpočtový prostor ukazuje soubor všech kombinací obou komodit, které lze zakoupit utrácením celého nebo části daného příjmu.
jinými slovy, rozpočtový prostor představuje příležitost stanovenou pro spotřebitele, tedy všechny kombinace dvou komodit, které může koupit, vzhledem k jeho rozpočtovému omezení. Rozpočtový prostor tedy znamená soubor všech kombinací dvou zboží, pro které příjmy vynaložené na dobré X (tj. PxX a příjmy vynaložené na dobré Y (tj.,
Proto můžeme algebraicky vyjádřit rozpočtu prostor v následující formě nerovnosti:
PxX + PyY < M, nebo M > PxX + PyY
REKLAMY:
cenově prostor byl graficky znázorněno na Obr. 8.15 jako stínovaná oblast. Rozpočtový prostor je celá oblast uzavřená rozpočtovou linkou BL a dvěma osami.
změny ceny a posun v rozpočtové linii:
nyní, co se stane s rozpočtovou linií, pokud se změní buď ceny zboží, nebo se změní příjem., Podívejme se nejprve na změny cen zboží. To je znázorněno na obr. 8.16. Předpokládejme, že rozpočtová čára na začátku je BL, vzhledem k určitým cenám zboží X a Y a určitému příjmu. Předpokládejme, že cena x klesá, cena Y a příjmy zůstávají nezměněny. Nyní, s nižší cenou X, bude spotřebitel moci koupit více množství X než dříve s daným příjmem.
nechte za nižší cenu X, daný příjem nakupuje OL ‚ X, který je větší než OL., Od té doby cena Y zůstává stejná, tam může být žádná změna v množství zakoupené dobrých Y se stejným vzhledem příjem, a jako výsledek tam bude žádný posun v bodě B. Tak, s poklesem ceny dobré X, spotřebitel, peníze, příjmy a ceny Y zbývající konstantní, linie rozpočtu se posune doprava na novou pozici BL‘.,
REKLAMY:
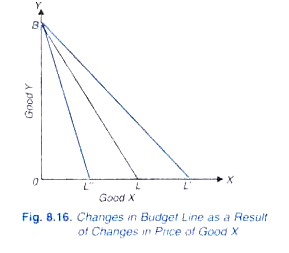
Nyní, co se bude dít na rozpočtové linie (initial budget line, BL), pokud je cena dobrá X stoupá, cena dobrá Y a příjmu zbývající nezměněné. S vyšší cenou good X může spotřebitel zakoupit menší množství X, řekněme OL “ než dříve. S nárůstem ceny X se tedy rozpočtová linie posune doleva na novou pozici BL“.
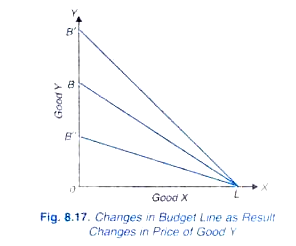
Obrázek 8.,17 ukazuje změny v rozpočtové linii, když cena dobrého Y klesá nebo stoupá, přičemž cena X a příjem zůstávají stejné. V tomto počátečním rozpočtovém řádku je BL. S poklesem ceny dobrého Y, ostatní věci zůstávají nezměněny, spotřebitel mohl koupit více Y s daným příjmem peněz, a proto se rozpočtová linie přesune nad LB“. Podobně, s nárůstem ceny Y, jiné věci jsou konstantní, rozpočtová linie se posune níže na LB“.,
REKLAMY:
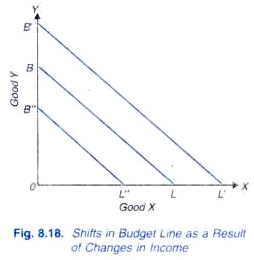
Změny v Příjmech a změny v Rozpočtové linii,
Nyní, otázka je, co se stane do rozpočtu řádku, pokud příjem změny, zatímco ceny zboží zůstávají stejné. Vliv změn příjmů na rozpočtovou linii je uveden na obr. 8.18. Nechť BL je počáteční rozpočtová linie, vzhledem k určitým cenám zboží a příjmů. Pokud se příjmy spotřebitelů zvýší, zatímco ceny zboží X I y zůstanou nezměněny, cenová linie se posune nahoru (řekněme na BL) a je rovnoběžná s původní rozpočtovou linií BL.,
je To proto, že se zvýšil příjem spotřebitele je možnost zakoupit úměrně větší množství dobré X, než když celý příjmu je vynaloženo na X, a úměrně větší množství dobrých Y, než kdyby celý příjmu je vynaloženo na Y. Na druhou stranu, pokud je příjem spotřebitele klesá, ceny zboží X a Y zůstanou beze změny, rozpočtové linie posune dolů (řekněme, na B“L“) ale zůstává rovnoběžná s původní cenou linku BL.,
je To proto, že nižší příjem bude nákup úměrně menší množství dobré, když X je celé z příjmů se vynakládá na X a úměrně menší množství dobrých Y v případě, že celá příjmu je vynaloženo na Y.
je zřejmé, že od výše rozpočtu, řádek se bude měnit, pokud se buď ceny zboží změnit nebo příjem spotřebitele změny.
REKLAMY:
to Znamená, že dva determinanty rozpočtové položky jsou:
(a) ceny zboží a
(b) spotřebitel příjmů musí být vynaložena na zboží.,
Sklon Linie Rozpočtu a Ceny Dvou Zboží:
je také důležité si uvědomit, že sklon rozpočtové linie se rovná poměru cen dvou statků. To lze prokázat pomocí obr. 8.14. Předpokládejme, že daný příjem spotřebitele Je M a dané ceny zboží X a Y jsou Px a Py.
sklon rozpočtové linie BL je OB / ol. Máme v úmyslu prokázat, že tento sklon se rovná poměru cen zboží X a Y.,
reklamy:
množství dobrého x zakoupeného, pokud je na něj vynaložen celý daný příjem M, je OL. Proto OL x Px = M
OL = M/Px
nyní je množství dobrého y zakoupeného, pokud se na něj vynakládá celý daný příjem M, OB.

je tedy prokázáno, že sklon rozpočtové linie BL se rovná poměru cen dvou zboží.
Napsat komentář