SPSS Correlation Analysis Tutorial (Čeština)

také viz Pearson korelace-rychlý úvod.

• korelační Test – Co to je?
• nulová hypotéza
• předpoklady
• korelační Test v SPSS
• hlášení

korelační Test – Co to je?

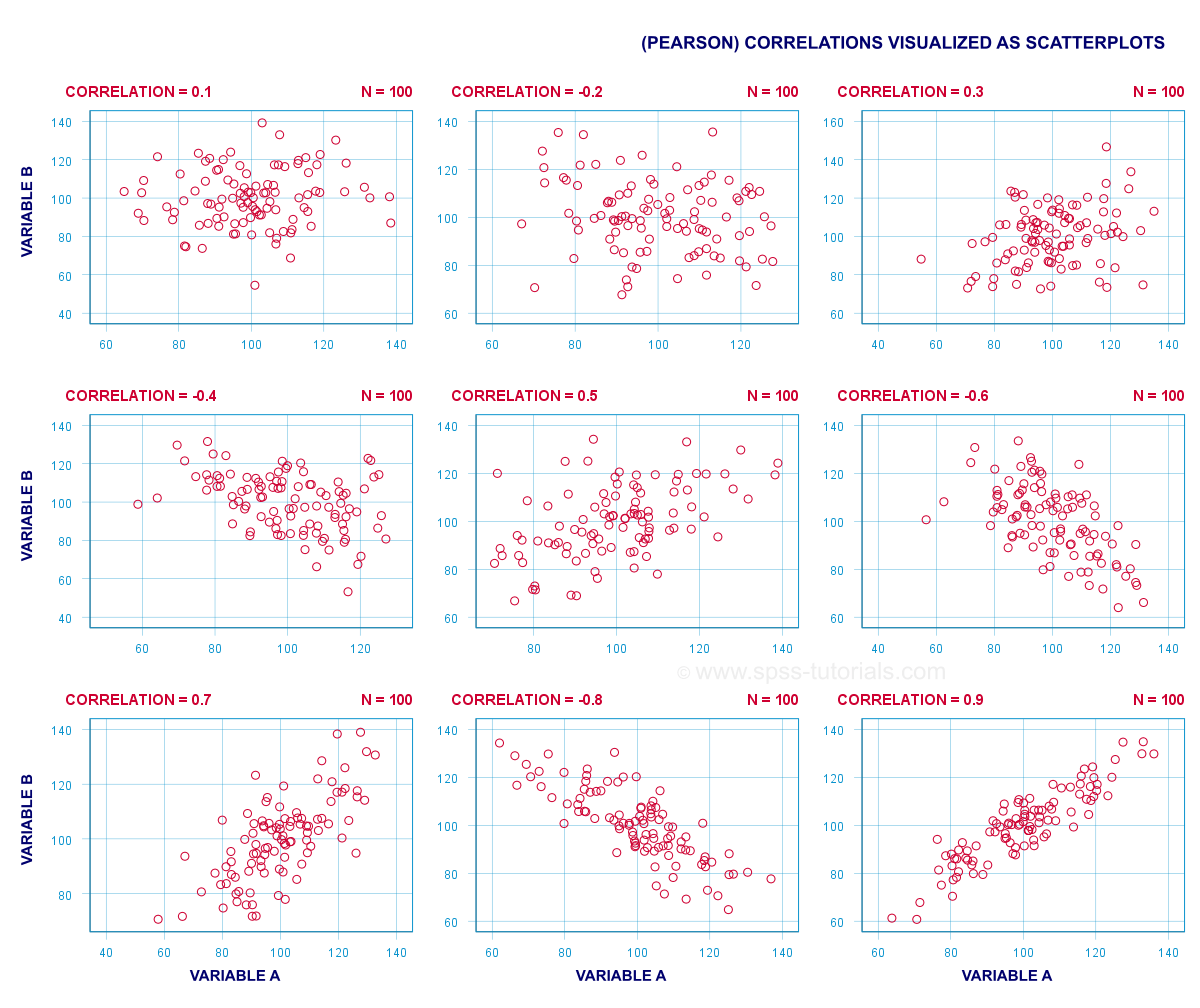
a (Pearson) korelace je číslo mezi -1 a + 1, které udává, do jaké míry jsou kvantitativní proměnné 2 lineárně příbuzné. To je nejlépe pochopit při pohledu na některé scatterplots.,

stručně řečeno,

• korelace -1 znamená dokonalou lineární klesající vztah: vyšší skóre na jedné proměnné znamená, že nižší skóre na druhé proměnné.
• korelace 0 znamená, že neexistuje žádný lineární vztah mezi 2 proměnnými. Může však existovat (silný) nelineární vztah.
• korelace 1 znamená dokonalý vzestupný lineární vztah: vyšší skóre na jedné proměnné je spojeno s vyššími skóre na druhé proměnné.,

nulová hypotéza

korelační test (obvykle) testuje nulovou hypotézu, že populační korelace je nulová.Data často obsahují pouze vzorek z (mnohem) větší populace: zkoumal jsem 100 zákazníků (vzorek), ale opravdu mě zajímají všichni moji zákazníci 100,000 (populace). Výsledky vzorků se obvykle poněkud liší od výsledků populace. Takže nalezení nenulové korelace v mém vzorku neprokazuje, že 2 proměnné korelují v celé mé populaci; pokud je populační korelace skutečně nulová, mohu snadno najít malou korelaci ve svém vzorku., Nalezení silné korelace v tomto případě je však velmi nepravděpodobné a naznačuje, že moje populační korelace nakonec nebyla nulová.

korelační Test-předpoklady

výpočet a interpretace korelačních koeficientů samy o sobě nevyžadují žádné předpoklady. Nicméně, statistické významnosti-test pro korelace předpokládá,

• nezávislé pozorování;
• normality: naše 2 proměnné musí následovat bivariate normální rozložení v naší populaci. Tento předpoklad není nutný pro velikosti vzorku N = 25 nebo více.,U rozumných velikostí vzorků centrální limitní věta zajišťuje, že rozdělení vzorku bude normální.

SPSS-Rychlá kontrola dat

pojďme nyní provést některé korelační testy v SPSS. Použijeme adolescenty.sav, datový soubor, který obsahuje údaje o psychologických testech 128 dětí ve věku 12 až 14 let. Část jeho variabilního zobrazení je uvedena níže.

před spuštěním jakýchkoli korelací se nejprve ujistěte, že naše data jsou v první řadě věrohodná., Protože všech 5 proměnných je metrických, rychle zkontrolujeme jejich histogramy spuštěním níže uvedené syntaxe.

výstup histogramu

naše histogramy nám hodně říkají: naše proměnné mají mezi 5 a 10 chybějícími hodnotami. Jejich prostředky jsou blízké 100 se standardními odchylkami kolem 15-což je dobré, protože takto byly tyto testy kalibrovány. Jedna věc mi vadí, ačkoli, a to je uvedeno níže.,

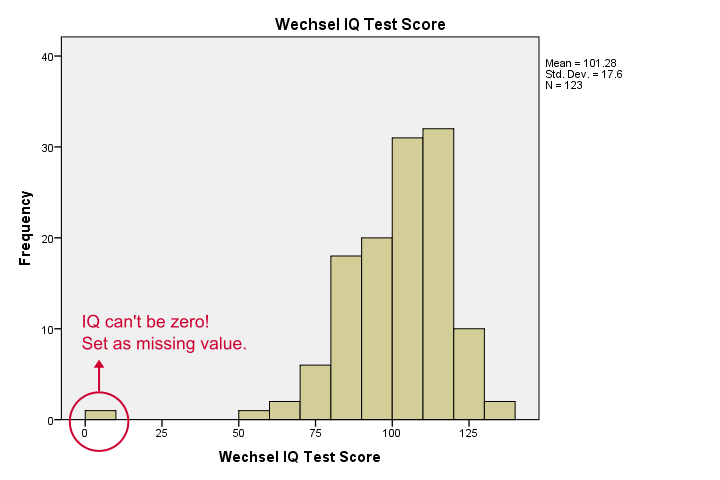
zdá se, že někdo zaznamenal nulu na některých testech-což není vůbec věrohodné. Pokud to budeme ignorovat, naše korelace budou vážně zkreslené. Pojďme třídit naše případy, uvidíme, co se děje a nastavit některé chybějící hodnoty před pokračováním.

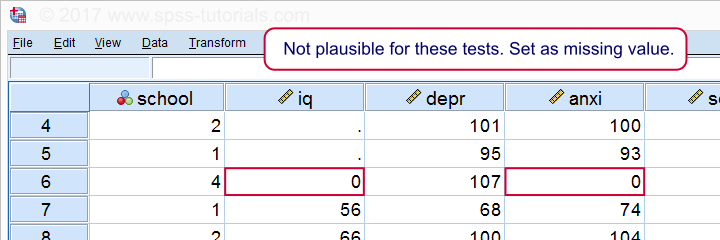
Pokud nyní opakujeme naše histogramy, uvidíme, že všechny distribuce vypadají věrohodně., Teprve teď bychom měli pokračovat v provádění skutečných korelací.

spuštění korelačního testu v SPSS

pojďme nejprve přejít na analýzu korelovat Bivariate, jak je uvedeno níže.

přesuňte všechny relevantní proměnné do pole proměnné. Pravděpodobně zde nechcete nic změnit.

kliknutím na Vložit výsledky v syntaxi níže. Projedeme to.

SPSS korelace syntaxe

korelační výstup

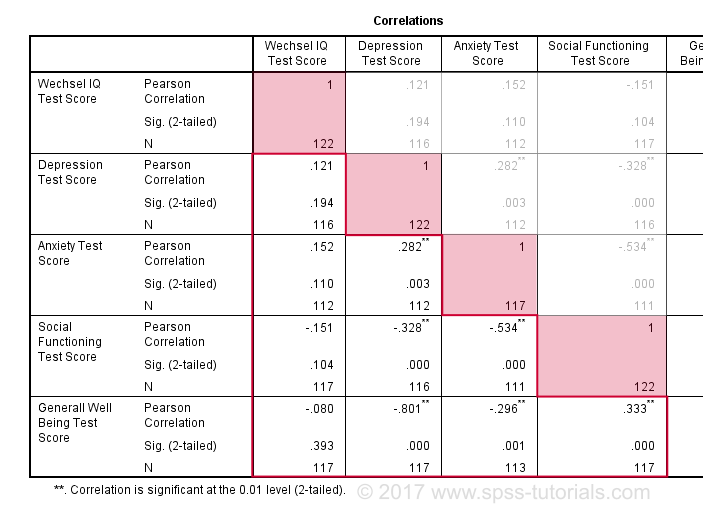
ve výchozím nastavení SPSS vždy vytvoří úplnou korelační matici. Každá korelace se objeví dvakrát: nad a pod hlavní úhlopříčkou. Korelace na hlavní diagonále jsou korelace mezi každou proměnnou a samotnou-proto jsou všechny 1 a vůbec zajímavé. 10 korelací pod úhlopříčkou je to, co potřebujeme., Zpravidla je korelace statisticky významná, pokud je její “ Sig. (2-sledoval)“ < 0.05.Nyní se podívejme na naše výsledky: nejsilnější korelace je mezi depresí a celkovou pohodou : r = -0.801. Je založen na n = 117 děti a jeho 2-sledoval význam, p = 0.000. To znamená, že existuje 0.000 pravděpodobnost nalezení této korelace vzorku-nebo větší-pokud je skutečná populační korelace nulová.
Všimněte si, že IQ nekoreluje s ničím. Jeho nejsilnější korelace je 0,152 s úzkostí, ale p = 0.,11 takže se statisticky významně neliší od nuly. To znamená, že existuje 0.11 šance na jeho nalezení, pokud je korelace populace nulová. Tato korelace je příliš malá na to, aby odmítla nulovou hypotézu.
tak, naše korelace 10 ukazují, do jaké míry je každý pár proměnných lineárně příbuzný. Nakonec si všimněte, že každá korelace je vypočtena na mírně odlišném N-v rozmezí od 111 do 117. Je to proto, že SPSS používá párové vymazání chybějících hodnot ve výchozím nastavení pro korelace.,

Scatterplots

přísně bychom měli zkontrolovat všechny scatterploty mezi našimi proměnnými. Koneckonců, proměnné, které nekorelují, by mohly být stále spojeny nějakým nelineárním způsobem. U více než 5 nebo 6 proměnných však počet možných rozptylů exploduje,takže je často přeskočíme. Nicméně, viz SPSS-vytvořit všechny Scatterplots nástroj.
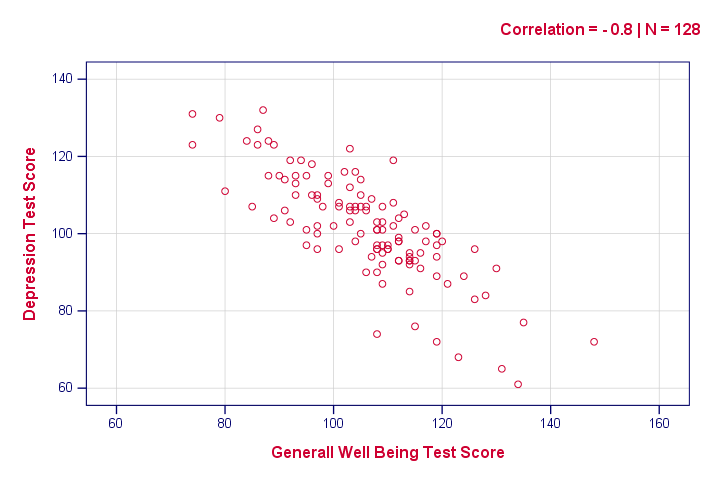
níže uvedená syntaxe vytváří pouze jeden scatterplot, jen aby si představu o tom, co náš vztah vypadá. Výsledek ale nic nečekaného nevykazuje.

vykazující korelační Test

níže uvedený obrázek ukazuje nejzákladnější formát doporučený APA pro vykazování korelací. Důležitější je, ujistěte se, že tabulka uvádí, které korelace jsou statisticky významné na p < 0,05 a možná p < 0.01. Viz také SPSS korelace ve formátu APA.

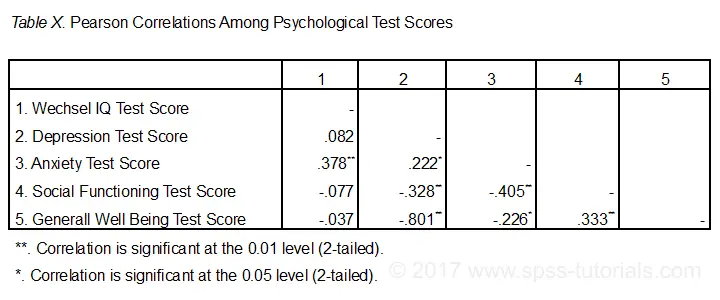
Pokud je to možné, nahlaste intervaly spolehlivosti také pro vaše korelace., Kupodivu, SPSS tyto nezahrnuje. Viz intervaly spolehlivosti SPSS pro nástroj korelace.

Díky za čtení!