Oversigt
- ulemperne ved frequentist statistik føre til, at behovet for Bayesiansk Statistik
- Oplev Bayesiansk Statistik og Bayesiansk Inferens
- Der er forskellige metoder til at teste betydningen af den model som p-værdi konfidensinterval, osv.
Indledning
Bayesiansk Statistik er fortsat uforståeligt i antændt sind af mange analytikere., At være forbløffet over den utrolige magt machine learning, en masse af os er blevet utro til statistik. Vores fokus er indsnævret til at udforske maskinindlæring. Er det ikke sandt?
vi forstår ikke, at maskinindlæring ikke er den eneste måde at løse problemer i den virkelige verden. I flere situationer hjælper det os ikke med at løse forretningsproblemer, selvom der er data involveret i disse problemer. For at sige det mildt, vil kendskab til statistikker give dig mulighed for at arbejde på komplekse analytiske problemer, uanset størrelsen af data.,
i 1770 ‘erne introducerede Thomas Bayes’Bayes sætning’. Selv efter århundreder senere er betydningen af ‘Bayesian Statistics’ ikke falmet væk. Faktisk bliver dette emne i dag undervist i store dybder i nogle af verdens førende universiteter.
med denne ID.har jeg oprettet denne begyndervejledning om Bayesian-statistik. Jeg har forsøgt at forklare begreberne på en forenklet måde med eksempler. Forudgående kendskab til grundlæggende Sandsynlighed & statistik er ønskeligt., Du bør tjekke dette kursus for at få en omfattende lav ned på statistik og sandsynlighed.
i slutningen af denne artikel vil du have en konkret forståelse af Bayesian-statistikker og dens tilknyttede begreber.,>Bayes Teorem
- Bernoulli sandsynligheden funktion
- Forudgående Tro Distribution
- Posterior tro Distribution
- p-værdi
- konfidensintervaller
- Bayes Faktor
- Høj Tæthed Interval (HDI)
Før vi rent faktisk dykke ned i Bayesiansk Statistik, lad os bruge et par minutter på at forstå Frequentist Statistik, mere populære version af statistikker, som de fleste af os er kommet på tværs, og den iboende problemer i det.,
Fre .uentist statistik
debatten mellem fre .uentist og bayesian har hjemsøgt begyndere i århundreder. Derfor er det vigtigt at forstå forskellen mellem de to, og hvordan findes der en tynd afgrænsningslinje!
det er den mest anvendte inferentielle teknik i den statistiske verden. Infact, generelt er det den første tankegang, at en person, der kommer ind i statistikverdenen, støder på.
Fre .uentist Statistics tester, om en begivenhed (hypotese) forekommer eller ej., Det beregner sandsynligheden for en begivenhed i det lange løb af eksperimentet (dvs.eksperimentet gentages under de samme betingelser for at opnå resultatet).
her tages prøveudtagningsfordelingerne af fast størrelse. Derefter gentages eksperimentet teoretisk uendeligt antal gange, men praktisk taget udført med en stoppende intention. For eksempel udfører jeg et eksperiment med en stoppende intention i tankerne om, at jeg vil stoppe eksperimentet, når det gentages 1000 gange, eller jeg ser minimum 300 hoveder i en møntkast.
lad os gå dybere nu.,
nu forstår vi fre .uentist-statistikker ved hjælp af et eksempel på møntkast. Målet er at estimere møntens retfærdighed. Nedenfor er en tabel, der repræsenterer hyppigheden af hoveder:

Vi ved, at sandsynligheden for at få et hoved på at kaste en fair mønt er 0,5. No. of heads repræsenterer det faktiske antal opnåede hoveder. Difference er forskellen mellem 0.5*(No. of tosses) - no. of heads.,
En vigtig ting er at bemærke, at selvom forskellen mellem det faktiske antal hoveder og forventede antal hoveder( 50% af antallet af kast), stiger, når antallet af kast er steget, er andelen af antallet af hoveder til det samlede antal kaster tilgange 0.5 (for en fair mønt).
dette eksperiment giver os en meget almindelig fejl, der findes i FRE .uentist-tilgang, dvs.afhængighed af resultatet af et eksperiment af antallet af gange eksperimentet gentages.,
for at vide mere om Fre .uentist statistiske metoder, kan du gå til dette fremragende kursus om inferentiel statistik.
de iboende fejl i FRE .uentiststatistikker
indtil her har vi kun set en fejl i FRE .uentiststatistikker. Det er kun begyndelsen.
20 århundrede oplevede en massiv stigning i frequentist statistik, der anvendes til numeriske modeller til at kontrollere, om en prøve, der er forskellig fra de andre, en parameter er vigtig nok til at blive holdt i modellen og variousother manifestationer af hypotese test., Men fre .uentist statistik lidt nogle store fejl i sit design og fortolkning, som udgjorde en alvorlig bekymring i alle virkelige problemer. For eksempel:
p-values måles med en prøve (fast størrelse) statistik med nogle stop hensigt ændringer med ændring i hensigt og stikprøvestørrelse. dvs.hvis to personer arbejder på de samme data og har forskellige stop-intentioner, kan de få to forskellige p- values for de samme data, hvilket er uønsket.,
For eksempel: Person A kan vælge at stoppe med at kaste en mønt, når det samlede antal når 100, mens B stopper ved 1000. For forskellige prøvestørrelser får vi forskellige t-scoringer og forskellige p-værdier. På samme måde kan intentionen om at stoppe ændre sig fra et fast antal flips til den samlede varighed af flipping. Også i dette tilfælde er vi nødt til at få forskellige p-værdier.
2 – konfidensinterval (C. I) som p-value afhænger meget af prøvestørrelsen., Dette gør stoppotentialet absolut absurd, da uanset hvor mange personer der udfører testene på de samme data, skal resultaterne være konsistente.
3 – konfidensintervaller (C. jeg) er ikke sandsynlighedsfordelinger de derfor ikke udgøre den mest sandsynlige værdi for en parameter og de mest sandsynlige værdier.
disse tre grunde er nok til at få dig til at tænke på ulemperne ved fre .uentist-tilgangen, og hvorfor er der behov for bayesian-tilgang. Lad os finde ud af det.,
herfra forstår vi først det grundlæggende i Bayesian-statistikker.
Bayesian Statistics
“Bayesian statistics er en matematisk procedure, der anvender sandsynligheder for statistiske problemer. Det giver folk værktøjer til at opdatere deres tro på bevis for nye data.”
har du det? Lad mig forklare det med et eksempel:
Antag, ud af alle de 4 championship races (F1) mellem Niki Lauda og James hunt, Niki vandt 3 gange, mens James lykkedes det kun for 1.,
så hvis du skulle satse på vinderen af næste løb, hvem ville han så være ?
Jeg vil vædde på du ville sige Niki Lauda.
her er T .ist. Hvad hvis du får at vide, at det regnede en gang, da James vandt, og en gang, da Niki vandt, og det er klart, at det regner på den næste dato. Så hvem vil du satse dine penge på nu ?
Af intuition, er det let at se, at chancerne for at vinde for James er steget drastisk. Men spørgsmålet er: hvor meget ?,
for at forstå problemet ved hånden skal vi blive bekendt med nogle begreber, hvoraf den første er betinget sandsynlighed (forklaret nedenfor).
derudover er der visse forudsætninger:
forudsætninger:
- Lineær Algebra : for at opdatere dine grundlæggende, kan du tjekke Khan ‘ s Academy Algebra.
- sandsynlighed og grundlæggende statistik : for at opdatere dine grundlæggende, kan du tjekke et andet kursus af Khan Academy.
3.,1 betinget sandsynlighed
det er defineret som: sandsynligheden for en begivenhed a givet B er lig med sandsynligheden for B og a sker sammen divideret med sandsynligheden for B.”
For eksempel: Antag to delvist skærende sæt A og B som vist nedenfor.
sæt A repræsenterer et sæt begivenheder, og sæt B repræsenterer et andet. Vi ønsker at beregne sandsynligheden for en given B er allerede sket. Lad os repræsentere begivenheden af begivenhed B ved at skygge den med rødt.,
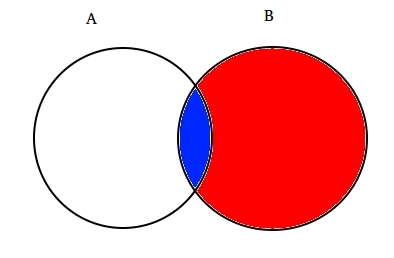
Nu da B er sket, er den del, der nu spørgsmål til En der er en del skyggefulde i blå, som er interessant ![]() . Så er sandsynligheden for, at En given B viser sig at være:
. Så er sandsynligheden for, at En given B viser sig at være:
Derfor, vi kan skrive formlen for hændelse B givet En allerede opstået ved:
eller
Nu, den anden ligning kan skrives som :
Dette er kendt som Betinget Sandsynlighed.,
lad os prøve at besvare et væddemålsproblem med denne teknik.
Antag, B være tilfælde af at vinde af James Hunt. En være tilfælde af regner. Derfor
ved at erstatte værdierne i den betingede sandsynlighedsformel får vi sandsynligheden for at være omkring 50%, hvilket er næsten det dobbelte af 25%, når der ikke blev taget hensyn til regn (Løs det ved din ende).
dette styrkede yderligere vores tro på, at James vandt i lyset af nye beviser, dvs.regn., Du skal undre dig over, at denne formel ligner noget, du måske har hørt meget om. Tænk!
sandsynligvis gættede du det rigtigt. Det ligner Bayes sætning.
Bayes sætning er bygget oven på betinget sandsynlighed og ligger i hjertet af Bayesian inferens. Lad os forstå det i detaljer nu.
3.2 Bayes Teorem
Bayes Teorem træder i kraft, når flere begivenheder danner et udtømmende sæt med en anden begivenhed, B. Dette kan forstås ved hjælp af nedenstående diagram.,

Nu, at B kan skrives som
Så sandsynligheden for, at B kan skrives som,
Men![]()
Så, udskiftning P(B) i ligningen for betinget sandsynlighed for, at vi får

Dette er ligningen for Bayes Teorem.
Bayesian inferens
der er ingen mening i at dykke ind i det teoretiske aspekt af det. Så vi lærer, hvordan det virker!, Lad os tage et eksempel på møntkast for at forstå ideen bag bayesian inferens.
en vigtig del af bayesian inferens er etablering af parametre og modeller.
modeller er den matematiske formulering af de observerede hændelser. Parametre er de faktorer i modellerne, der påvirker de observerede data. For eksempel ved at kaste en mønt kan retfærdighed af mønt defineres som parameteren for mønt betegnet med.. Resultatet af begivenhederne kan betegnes med D.
svar Dette nu., Hvad er sandsynligheden for 4 hoveder ud af 9 kaster (D) givet retfærdighed af mønt ()). dvs P(D|θ)
vent, stillede jeg det rigtige spørgsmål? Ingen.
at Vi bør være mere interesseret i at vide : Givet et resultat (D) hvad er den probbaility af mønten er fair (θ=0.5)
Lader repræsentere det ved hjælp af Bayes Teorem:
P(θ|D)=(P(D|θ) X P(θ))/P(D)
Her, P(θ) er inden i.e styrken af vores tro på retfærdigheden af mønt før lodtrækningen., Det er helt okay at tro, at coin kan have nogen grad af retfærdighed mellem 0 og 1.
P(D|θ) er sandsynligheden for at observere vores resultat i betragtning af vores fordeling for θ. Hvis vi vidste, at mønten var retfærdig, giver dette sandsynligheden for at observere antallet af hoveder i et bestemt antal flips.
P(D) er beviset. Dette er sandsynligheden for data som bestemt ved at opsummere (eller integrere) på tværs af alle mulige værdier af., vægtet af, hvor stærkt vi tror på de særlige værdier af θ.,
hvis vi havde flere visninger af, hvad retfærdigheden af mønten er (men ikke vidste med sikkerhed), fortæller dette OS sandsynligheden for at se en bestemt sekvens af flips for alle muligheder for vores tro på møntens retfærdighed.
P(θ|D) er den bageste tro på vores parametre efter at have observeret beviset, dvs.antallet af hoveder .
herfra vil vi dykke dybere ned i matematiske implikationer af dette koncept. Bare rolig. Når du forstår dem, er det ret nemt at komme til matematik.,
for at definere vores model korrekt har vi brug for to matematiske modeller før hånden. En til at repræsentere sandsynligheden funktion P (D/)) og den anden til at repræsentere fordelingen af tidligere overbevisninger . Produktet af disse to giver den bageste tro P (|/d) distribution.
da tidligere og posterior begge er overbevisninger om fordelingen af retfærdighed af mønt, fortæller intuition os, at begge skal have den samme matematiske form. Husk dette. Vi vil vende tilbage til det igen.,
så der er flere funktioner, der understøtter eksistensen af bayes sætning. At kende dem er vigtigt, derfor har jeg forklaret dem detaljeret.
4. 1. Bernoulli Sandsynlighed funktion
lader opsummere, hvad vi lærte om sandsynligheden funktion. Så, vi har lært at:
Det er sandsynligheden for at observere et bestemt antal hoveder i et bestemt antal vender for en given retfærdighed mønt. Det betyder, at vores Sandsynlighed for at observere plat/krone afhænger af retfærdigheden af mønt ()).,
P(y=1|θ)=
P(y=0|θ)=
det er værd at bemærke, at det at repræsentere 1 som hoveder og 0 som haler kun er en matematisk notation til at formulere en model. Vi kan kombinere de ovennævnte matematiske definitioner i en enkelt definition for at repræsentere sandsynligheden for begge resultater.
P(y|θ)=
Dette kaldes Bernoulli Sandsynligheden for, Funktion og opgave af mønten spejlvende kaldes Bernoulli forsøg.,
y={0,1},θ=(0,1)
Og når vi ønsker at se en række hoveder eller vipper, dens sandsynlighed er givet ved:
Desuden, hvis vi er interesseret i sandsynligheden for at antallet af hoveder z dreje op i N antallet af vipper så er sandsynligheden givet ved:
4.2. Tidligere trosfordeling
denne distribution bruges til at repræsentere vores styrker på overbevisninger om parametrene baseret på den tidligere erfaring.,
men hvad nu hvis man ikke har nogen tidligere erfaring?
bare rolig. Matematikere har udtænkt metoder til at afbøde dette problem også. Det er kendt som uninformative priors. Jeg vil gerne informere dig på forhånd om, at det bare er en misvisende. Hver uninformative prior altid giver nogle oplysninger begivenhed den konstante fordeling forudgående.
Nå er den matematiske funktion, der bruges til at repræsentere de tidligere overbevisninger, kendt som beta distribution., Det har nogle meget flot matematiske egenskaber, som gør det muligt for os at modellere vores overbevisninger om en binomial fordeling.
sandsynlighedsdensitetsfunktionen for beta-distribution er af formen:
hvor vores fokus forbliver på tæller. Nævneren er der bare for at sikre, at den samlede sandsynlighedstæthed funktion ved integration evaluerer til 1.
α og β kaldes den form beslutter parametre for tæthedsfunktionen., Her α svarer til antallet af hoveder i forsøgene og β svarer til antallet af haler., Diagrammerne nedenfor vil hjælpe dig med at visualisere beta-distributioner til forskellige værdier af α og β

Du kan også trække beta-fordeling for dig selv ved hjælp af følgende kode i R:
Bemærk: α og β er intuitiv at forstå, da de kan beregnes ved at kende middel (μ) og standardafvigelse (σ) af fordelingen., Faktisk er de relateret til :
Hvis middel-og standardafvigelse for en distribution er kendt , kan formparametre let beregnes.
inferens trukket fra grafer ovenfor:
- da der ikke var nogen kast, troede vi, at enhver retfærdighed af mønt er mulig som afbildet af den flade linje.
- når der var mere antal hoveder end halerne, viste grafen en top forskudt mod højre side, hvilket indikerer højere sandsynlighed for hoveder, og at mønten ikke er retfærdig.,
- efterhånden som flere kaster er færdige, og hoveder fortsætter med at komme i større andel, indsnævres toppen og øger vores tillid til rimeligheden af møntværdien.
4.3. Posterior trosfordeling
grunden til, at vi valgte tidligere tro, er at opnå en beta-distribution. Dette skyldes, at når vi multiplicerer det med en sandsynlighedsfunktion, giver posterior distribution en form, der ligner den tidligere distribution, som er meget lettere at forholde sig til og forstå., Hvis denne meget information whhets din appetit, jeg er sikker på du er klar til at gå en ekstra mile.
lad os beregne posterior tro ved hjælp af bayes sætning.
beregning af posterior tro ved hjælp af Bayes Theorem
nu bliver vores bageste tro,
dette er interessant., Bare ved at kende middelværdien og standardfordelingen af vores tro på parameteren θ og ved at observere antallet af hoveder i N flips, kan vi opdatere vores tro på modelparameteren(θ).
lad os forstå dette ved hjælp af et simpelt eksempel:
Antag, at du tror, at en mønt er forudindtaget. Det har en gennemsnitlig (μ) bias på omkring 0,6 med standardafvigelse på 0,1.
Så
α= 13.8 β=9.2
jeg har.,e vores distribution vil være forudindtaget på højre side. Antag, at du observerede 80 hoveder (z=80) i 100 flips (N=100). Lad os se, hvordan vores forudgående og posterior overbevisninger kommer til at se:
prior = P(θ|α,β)=P(θ|13.8,9.2)
Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)
lad os visualisere både de overbevisninger på en graf:

Den R kode for ovenstående graf er:
}
efterhånden Som flere og flere vender, og at nye data, der er observeret, vil vores tro blive opdateret., Dette er den virkelige kraft af Bayesian inferens.
Test for Betydning – Frequentist vs Bayesian
Uden at gå ind i den stringente matematiske strukturer, vil dette afsnit give dig et hurtigt overblik over de forskellige tilgange til frequentist og bayesianske metoder til at teste for signifikans og forskel mellem grupper og hvilken metode, der er mest pålidelig.
5, 1. p-værdi
i dette beregnes t-score for en bestemt prøve fra en prøveudtagningsfordeling af fast størrelse. Derefter forudsiges p-værdier., Vi kan fortolke p-værdier som (idet der tages et eksempel på p-værdi som 0,02 for en fordeling af middel 100): der er 2% Sandsynlighed for, at prøven vil have middelværdi svarende til 100.
Denne fortolkning lider af den fejl, som for samplingfordelinger af forskellige størrelser, den ene er bundet til at få forskellige t-score og dermed forskellige p-værdi. Det er fuldstændig absurd. En p-værdi mindre end 5% garanterer ikke, at nulhypotesen er forkert, og en p-værdi større end 5% sikrer, at nulhypotesen er rigtig.
5.2., Konfidensintervaller
konfidensintervaller lider også af den samme defekt. Desuden Da C. I er ikke en sandsynlighedsfordeling, der er ingen måde at vide, hvilke værdier er mest sandsynlige.
5.3. Bayes Factor
Bayes factor svarer til p-værdi i bayesian-rammen. Lad os forstå det på en omfattende måde.
nulhypotesen i bayesian rammer forudsætter, ∞ sandsynlighedsfordeling kun ved en bestemt værdi af en parameter (sige θ=0.5) og en nul sandsynlighed andet sted, hvor., (M1)
den alternative hypotese er, at alle værdier af θ er mulige, og dermed en flad kurve, der repræsenterer fordelingen. (M2)
nu ser posterior distribution af de nye data ud nedenfor.

Bayesiansk statistik justeret troværdighed (sandsynlighed) for forskellige værdier af θ. Det kan let ses, at sandsynlighedsfordelingen er skiftet mod M2 med en værdi højere end M1 dvs.M2 er mere tilbøjelige til at ske.,
Bayes faktor afhænger ikke af den faktiske fordeling værdier af θ men størrelsen af forskydningen i værdier af M1 og M2.
i panel a (vist ovenfor): venstre bjælke (M1) er den forudgående Sandsynlighed for nulhypotesen.
i panel B (vist) er den venstre bjælke den bageste Sandsynlighed for nulhypotesen.
Bayes-faktor defineres som forholdet mellem de bageste odds og de tidligere odds,
for at afvise en nulhypotese foretrækkes en BF < 1/10.,
Vi kan se de umiddelbare fordele ved at bruge Bayes Faktor i stedet for p-værdier, da de er uafhængige af intentioner og stikprøvestørrelse.
5.4. Højdensitetsinterval (HDI)
HDI dannes fra den bageste distribution efter at have observeret de nye data. Da HDI er en sandsynlighed, giver 95% HDI de 95% mest troværdige værdier. Det er også garanteret, at 95% af værdierne vil ligge i dette interval, i modsætning til C. I.
Meddelelse, hvor de 95% HDI i tidligere distribution er større end 95% posterior fordeling., Dette skyldes, at vores tro på HDI øges ved observation af nye data.

Afslut Noter
formålet med denne artikel var at få dig til at tænke over de forskellige typer af statistiske filosofier derude, og hvordan en enkelt af dem kan bruges i enhver situation.
det er på høje tid, at begge filosofier fusioneres for at afbøde de virkelige verdensproblemer ved at tackle manglerne i den anden., Del II i denne serie vil fokusere på dimensionalitet reduktionsteknikker ved hjælp af MCMC (Markov Chain Monte Carlo) algoritmer. Del III vil være baseret på at skabe en Bayesian regressionsmodel fra bunden og fortolke dens resultater i R. Så før jeg starter med Del II, vil jeg gerne have dine forslag / feedback på denne artikel.
Skriv et svar