|
“Bi” betyder “to” (som en cykel har to hjul) … |
 |

kast med en Mønt:
- får vi Lederne (H) eller
- Haler (T)
Vi sige, at sandsynligheden for at mønten lander H er ½
Og sandsynligheden for at mønten lander T er ½
Lad os Kaste en Mønt!
Kast en fair mønt tre gange … hvad er chancen for at få to hoveder?,tr>












Which outcomes do we want?,
“to hoveder” kunne være i enhver rækkefølge: “HHT”, “THH” og “HTH” har alle to hoveder (og en hale).
så 3 af resultaterne producerer “to hoveder”.
hvad er sandsynligheden for hvert resultat?,selskaber er (P betyder “Sandsynlighed”):
- P(Tre Hoveder) = P(HHH) = 1/8
- P(To Hoveder) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
- S(Hoved) = P(HTT) + P(THT) + P(TTT) = 1/8 + 1/8 + 1/8 = 3/8
- P(Nul Hoveder) = P(TTT) = 1/8
Vi kan skrive dette i form af en stokastisk Variabel, X = “antallet af Hoveder fra 3 kast af en mønt”:
- P(X = 3) = 1/8
- P(X = 2) = 3/8
- P(X = 1) = 3/8
- P(X = 0) = 1/8
Og dette er, hvad det ser ud som en graf:
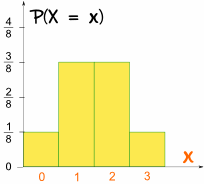
Det er symmetrisk!,
at lave en formel
forestil dig nu, at vi vil have chancerne for 5 hoveder i 9 kast: at liste alle 512 resultater vil tage lang tid!
så lad os lave en formel.
i vores tidligere eksempel, hvordan kan vi få værdierne 1, 3, 3 og 1 ?
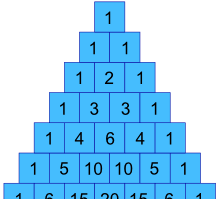
Nå, de er faktisk i Pascals trekant !
kan vi lave dem ved hjælp af en formel?
Sikker på, at vi kan, og her er det:
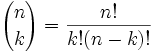
Det er ofte kaldet “n vælg k”
- n = samlede antal
- k = antal vi ønsker
- den “!,”betyder ” factorial”, for eksempel 4! = 1×2×3×4 = 24
Du kan læse mere om det på kombinationer og permutationer.
lad os prøve det:
lad os bruge det til et sværere spørgsmål:
Bias!
indtil videre har chancerne for succes eller fiasko været lige så sandsynlige.
men hvad nu hvis mønterne er forudindtaget (lander mere på den ene side end en anden) eller valg er ikke 50/50.
eksempel: du sælger sand .ich. 70% af mennesker vælger kylling, resten vælger noget andet.
Dette er ligesom eksemplet med hoveder og haler, men med 70/30 i stedet for 50/50.,
lad os tegne et trædiagram:
de “to kylling” sager er fremhævet.
sandsynlighederne for “to kyllinger” er alle 0.147, fordi vi multiplicerer to 0.7 s og en 0.3 i hvert tilfælde. Med andre ord
0.147 = 0.7 × 0.7 × 0.3
Eller ved hjælp af eksponenter:
= 0.72 × 0.31
0,7 er sandsynligheden for hvert valg, vi ønsker, kalder det p
Den 2 er antallet af valg, vi ønsker, kald det k
Og vi har (indtil videre):
= pk x 0.31
0.,3 er sandsynligheden for det modsatte valg, så er det: 1−p
1 er antallet af modsatte valg, så det er: n−k
Som giver os:
= pk(1-p)(n-k)
Hvor
- p er sandsynligheden for hvert valg, vi ønsker
- k er antallet af valg, vi ønsker
- n er det samlede antal af valgmuligheder
Nu kender vi sandsynligheden for hvert udfald er 0.147
OK. Det var meget arbejde for noget, vi allerede vidste, men nu har vi en formel, vi kan bruge til hårdere spørgsmål.,
sætte det sammen
nu ved vi, hvordan man beregner hvor mange:
n!k!(n-k)!
Og sandsynligheden for hver:
pk(1-p)(n-k)
Når ganget sammen får vi:
Sandsynligheden for at k ud af n måder:
P(k ud af n) = n!k!(n-k)! pk(1-p)(n-k)
Den Generelle Binomial Sandsynlighed Formel
Vigtigt:
- De forsøg, der er uafhængige,
- Der er kun to mulige udfald i hvert forsøg,
- sandsynligheden for “succes” ved hvert forsøg er konstant.,
Quuincun.

har et spil med Quuincun. (læs derefter Explaineduincun. forklaret) for at se Binomialfordelingen i aktion.
kast terningen
en fair terning kastes fire gange. Beregn sandsynlighederne for at få:
- 0 Toere
- 1 To
- 2 Toere
- 3 Toere
- 4 Toere
I dette tilfælde er n=4, p = p(To) = 1/6
X er den stokastiske Variabel ‘Antal Toere fra fire kaster’.,
Erstat = = 0 til 4 i formlen:
P(k ud af n) = n!k!(n-k)! pk(1-p) (n-k)
som denne (til 4 decimaler):
denne gang er grafen ikke symmetrisk:
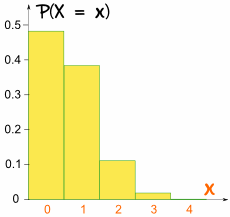
det er ikke symmetrisk!
det er skævt, fordi p ikke er 0,5

sportscykler
din virksomhed laver sportscykler. 90% passerer endelig inspektion (og 10% mislykkes og skal fastsættes).
Hvad er den forventede gennemsnit og variation af de 4 Næste inspektioner?lad os først beregne alle sandsynligheder.,
- n = 4,
- p = p(Pass) = 0, 9
is er den tilfældige variabel “antal passager fra fire inspektioner”.
Erstat = = 0 til 4 i formlen:
P(k ud af n) = n!k!(n-k)! pk(1-p)(n-k)
Middelværdi, Varians og Standardafvigelse
Lad os beregne Middelværdi, Varians og Standardafvigelse for Sports Cykel inspektioner.
Der er (relativt) enkle formler til dem. De er lidt svære at bevise, men de arbejder!,
Det betyder, eller “forventet værdi” er:
μ = np
formlen for Variansen er:
Varians: σ2 = np(1-p)
Og standardafvigelsen er kvadratroden af variansen:
σ = √(np(1-p))
Til sports cykler:
Varians: σ2 = 4 × 0.9 × 0.1 = 0.36
Standard Afvigelsen er:
σ = √(0.36) = 0.6


Skriv et svar