Determinant af en Matri.

determinanten af en Matri. er et specielt tal, der kan beregnes ud fra en firkantet Matri..

En Matrix er en bred vifte af numre:

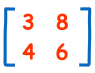
En Matrix
(Denne ene har 2 Rækker og 2 Kolonner)

determinanten af denne matrix er (beregninger er forklaret senere):

3×6 − 8×4 = 18 − 32 = -14

Hvad er det for?

determinanten hjælper os med at finde den inverse af en Matri., fortæller os ting om Matri theen, der er nyttige i systemer med lineære ligninger, beregning og mere.,

Symbol

symbolet for determinant er to lodrette linjer på hver side.

eksempel:<|p>

| A/betyder matrixens determinant a

(nøjagtigt det samme symbol som absolut værdi.)

beregning af determinanten

først og fremmest skal Matri .en være firkantet (dvs.have det samme antal rækker som kolonner). Så er det bare grundlæggende aritmetik., remember when you think of a cross:

Blue is positive (+ad),
Red is negative (−bc)

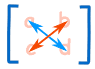
Example:

|B|= 4×8 − 6×3

= 32 − 18

= 14

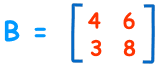
For a 3×3 Matrix

For a 3×3 matrix (3 rows and 3 columns):

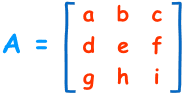
The determinant is:

|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
“The determinant of A equals .,.. osv.”

Det ser måske kompliceret, men der er et mønster:

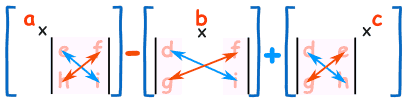
At finde ud af determinant af en 3×3 matrix:

Formere en af determinant af 2×2 matrix, der ikke er i a ‘ s række eller kolonne.
ligeledes for b og for c
opsummere dem, men husk minus foran b

<| ul>

som en formel (husk de lodrette bjælker | /betyder “determinant af”):

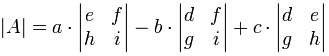
“determinanten for a er lig med en gange determinanten af …,

= -306

For 4×4 Matricer og Højere

Det mønster fortsætter i 4×4 matricer:

plus en times determinanten af den matrix, der ikke er i a ‘s række eller kolonne,
minus b gange determinanten af den matrix, der ikke er i b’ s række eller kolonne,
plus c gange determinanten af den matrix, der ikke er i c ‘s række eller kolonne,
minus d gange determinanten af den matrix, der ikke er i d’ s række eller kolonne,

Som en formel:

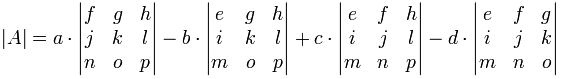
Bemærk +−+− mønster (+en.,.. – b… + c… −g…). Dette er vigtigt at huske.

mønsteret fortsætter i 5 5 5 matricer og højere. Normalt bedst at bruge en Matri calcul lommeregner for dem!

ikke den eneste måde

denne beregningsmetode kaldes “Laplace-udvidelsen”, og jeg kan godt lide det, fordi mønsteret er let at huske. Men der er andre metoder (bare så du ved det).,

Oversigt

For en 2×2 matrix, determinanten er ad – bc

For en 3×3 matrix, der ganger a med determinant af 2×2 matrix, der ikke er i a ‘ s række eller kolonne, ligeledes for b og c, men husk, at b har et negativt fortegn!

mønsteret fortsætter for større matricer: multiplicer A med determinanten af Matri .en, der ikke er i a ‘ S række eller kolonne, fortsæt sådan på tværs af hele rækken, men husk + − + − mønsteret.