|
To trekanter er kongruente, hvis de har:
men vi behøver ikke at kende alle tre sider og alle tre vinkler …normalt er tre ud af de seks nok. |
Der er fem måder at finde ud af, hvis to trekanter er kongruente: SSS, SAS, ASA, AAS og HL.,
VÆRDIPAPIRAFVIKLINGSSYSTEM (side side side)
SSS står for “side, side om side” og betyder, at vi har to trekanter med alle tre sider lige store.
For eksempel:
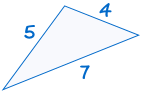 |
er kongruent til: | 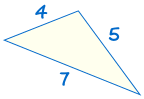 |
(Se Løsning af SSS Trekanter for at finde ud af mere)
Hvis tre sider i en trekant er lig med tre sider i den anden trekant, trekanter er kongruente.,
SAS (side -, vinkel-side)
SAS står for “side -, vinkel-side”, og betyder, at vi har to trekanter, hvor vi kender to sider, og de indgår vinkel er lige.,
For eksempel:
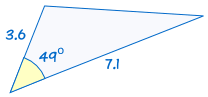 |
er kongruent til: | 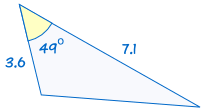 |
(Se Løsning af SAS Trekanter for at finde ud af mere)
Hvis to parter, og i prisen vinkel i en trekant er lig med den tilsvarende sider og en vinkel i en anden trekant, trekanter er kongruente.,
ASA (vinkel -, side -, vinkel)
ASA står for “vinkel, side -, vinkel” og betyder, at vi har to trekanter, hvor vi kender to vinkler og den medfølgende side er lige.,
For eksempel:
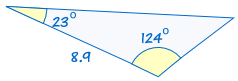 |
er kongruent til: | 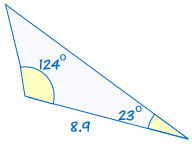 |
(Se Løsning af ASA Trekanter for at finde ud af mere)
Hvis to vinkler og den medfølgende side af en trekant er lig med den tilsvarende vinkler og siden af en anden trekant, trekanter er kongruente.,
AAS (vinkel, vinkel, side)
AAS står for “vinkel, vinkel, side” og betyder, at vi har to trekanter, hvor vi kender to vinkler og den manglende side i prisen er lige.,
For eksempel:
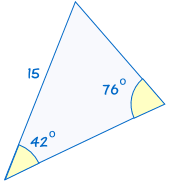 |
er kongruent til: | 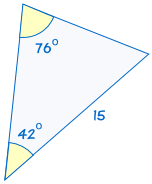 |
(Se Løsning af AAS Trekanter for at finde ud af mere)
Hvis to vinkler og den ikke-inkluderet side af en trekant er lig med den tilsvarende vinkler og siden af en anden trekant, trekanter er kongruente.
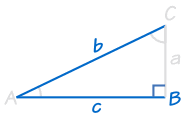
HL (hypotenuse, leg)
denne gælder kun for retvinklede trekanter!,
 |
eller | 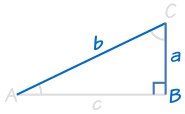 |
HL står for “Hypotenusen, Ben” (den længste side af en retvinklet trekant kaldes “hypotenusen”, og de to andre sider er de såkaldte “ben”)
Det betyder, at vi har to retvinklede trekanter med
- de samme længden af hypotenusen og
- samme længde for en af de to andre ben.
det er ligegyldigt hvilket ben, da trekanterne kunne drejes.,
For eksempel:
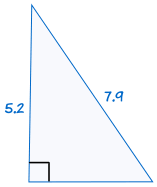 |
er kongruent til: | 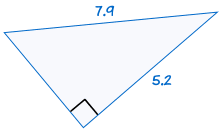 |
(se Pythagoras’ sætning for at finde ud af mere)
Hvis hypotenusen og et ben af en retvinklet trekant er lig med den tilsvarende hypotenuse og ben af en anden retvinklet trekant, er de to trekanter kongruente.
forsigtig! Brug ikke “AAA”
AAA betyder, at vi får alle tre vinkler i en trekant, men ingen sider.,
Dette er ikke nok information til at afgøre, om to trekanter er kongruente!
Fordi trekanter kan have de samme vinkler, men være forskellige størrelser:
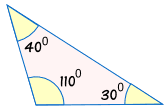 |
er ikke kongruent: | 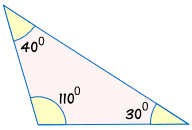 |
Uden at vide mindst én side, vi kan ikke være sikker på, at hvis to trekanter er kongruente.





Skriv et svar