Lyd Hastighed i Gasser

lydens hastighed i en ideal gas er givet ved forholdet

Vis

• R = den universelle gaskonstant = 8.314 J/mol K,
• T = den absolutte temperatur
• M = molekylvægten af den gas i kg/mol
• γ = den adiabatiske konstant, karakteristisk for den specifikke gas

For luften, til de adiabatiske konstant γ = 1.,4 og den gennemsnitlige molekylmasse for tør luft er 28,95 gm / mol. Dette fører til, at

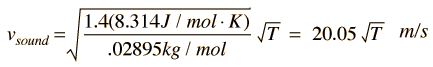
at Gøre denne beregning for luft ved 0°C giver vsound = 331.39 m/s og i 1°C giver vsound = 332.00 m/s., Dette fører til en almindeligt anvendt tilnærmede formel for den forsvarlige hastighed i luft:

Til temperaturer nær stuetemperatur, lydens hastighed i luft kan beregnes ud fra denne bekvemme omtrentlige forhold, men de mere generelle forhold, der er behov for beregninger i helium eller andre gasser.

beregningen ovenfor blev foretaget for tør luft, og fugtindholdet i luften forventes at øge lydens hastighed lidt, fordi vanddampens molekylvægt er 18 sammenlignet med 28.,95 for tør luft. En revideret gennemsnitlig molekylvægt kunne beregnes ud fra damptrykket af vand i luften. Men den antagelse af en adiabatisk konstant γ = 1,4 anvendes i beregningen er baseret på de diatomiske molekyler N2 og O2 og gælder ikke for vandmolekyler. Så den detaljerede modellering af virkningen af vanddamp på lydens hastighed ville være nødt til at afregne en passende værdi af γ til brug.