Pythagoras ‘Sætning

En af de bedst kendte matematiske formler, der er Pythagoras’ Sætning, der giver os med forholdet mellem siderne i en retvinklet trekant. En højre trekant består af to ben og en hypotenuse. De to ben mødes i en 90 angle Vinkel, og hypotenusen er den længste side af den rigtige trekant og er siden modsat den rigtige vinkel.,

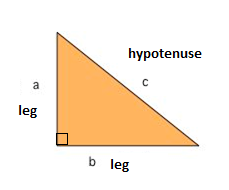
Den Pythagoræiske Læresætning fortæller os, at forholdet i hver retvinklet trekant er:

$$a^{2}+b^{2}=c^{2}$$

Eksempel

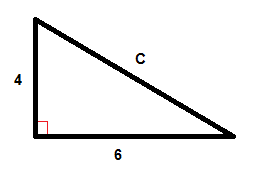
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$K=\sqrt{52}$$

$$C\ca 7.2$$

Der er et par specielle typer af højre trekanter, som det 45°og -45°, lige, trekanter og 30°-60° til højre trekant.,

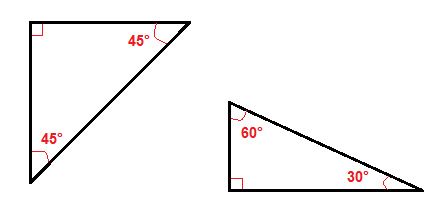
På grund af deres vinkler er det lettere at finde hypotenusen eller benene i disse højre trekanter end i alle andre højre trekanter.

i en 45–45.højre trekant behøver vi kun at multiplicere et ben med 2 2 for at få længden af hypotenusen.

Eksempel

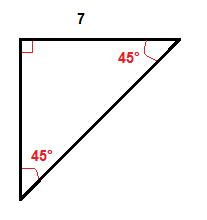
Vi ganger længden af benet, der er 7 inches med √2 for at få længden af hypotenusen.

$$7 \ cdot \s {rt{2} \ ca 9.,9$$

I en 30°-60° retvinklet trekant, kan vi finde længden af benet, der ligger over 30° vinkel ved hjælp af denne formel:

$$a=\frac{1}{2}\cdot c$$

Eksempel

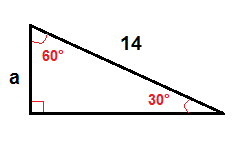
for At finde en, vi bruger formlen ovenfor.

$$a=\frac{1}{2} \ cdot 14$$

$ $ a=7 $ $

Video lektion

Find siderne af denne højre trekant