i denne lektion skal vi konstruere de fem (5) fælles logiske forbindelser eller operatører. De betragtes som almindelige logiske forbindelser, fordi de er meget populære, nyttige og altid undervises sammen.før vi begynder, foreslår jeg, at du gennemgår min anden lektion, hvor linket er vist nedenfor.
denne indledende lektion om sandhedstabeller indeholder forudsætningskendskab eller information, der hjælper dig med bedre at forstå indholdet af denne lektion.,
Introduktion til sandhedstabeller, udsagn og forbindelser
Le ‘ s start med at angive de fem (5) fælles logiske forbindelser.
De Fem (5) Fælles Logisk Connectives eller Operatører
- Logiske Negation
- Logisk Konjunktion (OG)
- Logisk Disjunktion (Inklusiv ELLER)
- Logisk Konsekvens (Betinget)
- Logisk Biconditional (Dobbelt-Implikation)
I., Sandhedstabel med logisk Negation
negationen af en erklæring er også en erklæring med en sandhedsværdi, der er nøjagtigt modsat den oprindelige erklæring. For eksempel skrives negationen af udsagnet symbolsk som
~\stort{p} eller \stort{\neg p}.
~{P} eller {\neg P} læses som “not S.”
Husk: for negation operatør angivet ved symbolet ~ eller \neg tager sandheden værdien af den oprindelige erklæring derefter output præcis det modsatte af dens sandheds-værdi., Med andre ord vender negation simpelthen sandhedsværdien af en given erklæring. Således, hvis erklæring P er sandt, er sandhedsværdien af dens negation falsk. På samme måde, hvis P er falsk, er sandhedsværdien af dens negation sand.

II. Sandhedstabel for Logisk Sammenhæng
En forbindelse er en type sætning, der består af to udsagn (også kendt som simple sætninger) følgeskab af OG operatør.,
symbolet, der bruges til at repræsentere og eller logisk konjunktionsoperatør, er \color{red}\Large{\wededge}. Det ligner et omvendt V.
Hvis vi har to enkle udsagn P og Q, og vi ønsker at danne en sammensat sætning følgeskab af OG operatøren, kan vi skrive det som:
\large{P \wedge Q}.
{p \wededge}} læses som “p og..”
husk: sandhedsværdien af den sammensatte sætning P \wededge.er kun sand, hvis sandhedsværdierne P og. begge er sande., Ellers er p \wededge false falsk.bemærk i sandhedstabellen nedenfor, at når P er sandt og Q er sandt, er P \wededge.sandt. Men de tre andre kombinationer af udsagn P og Q er falske.

III. Sandhedstabel for Logisk Disjunktion
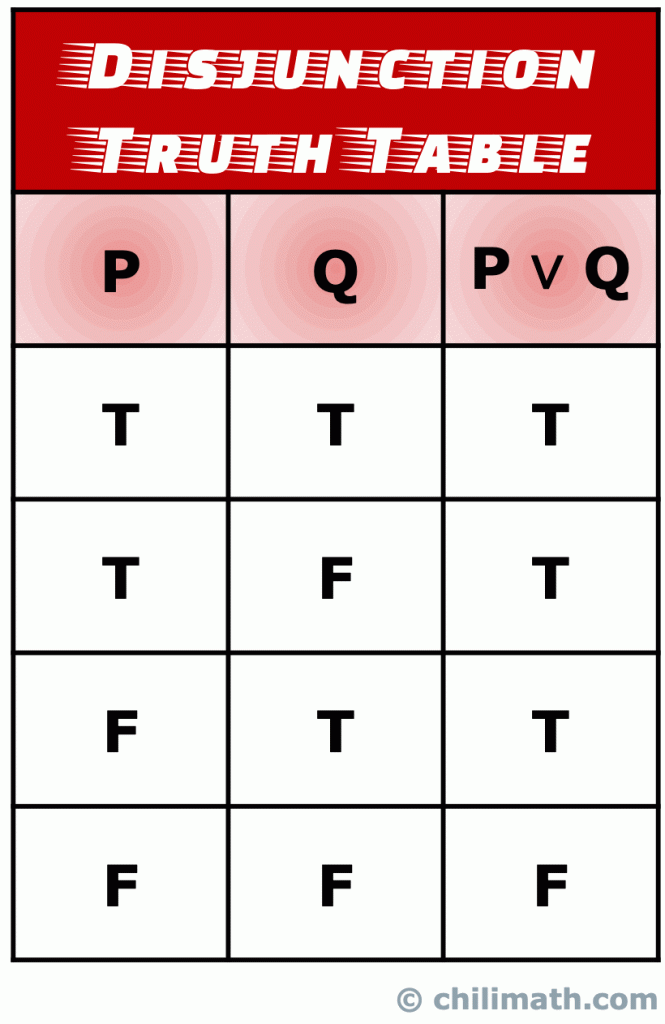
En disjunktion er en slags sammensat sætning, der er sammensat af to simple sætninger dannes ved at deltage i de erklæringer med ELLER operatør.
i en disjunction erklæring, brugen af eller er inklusiv. Det betyder “den ene eller den anden” eller begge dele.,
symbolet, der bruges til at repræsentere eller eller logisk disjunction operatør er \color{red}\Large{ \vee }. Det ligner bogstavet V i alfabetet.
to udsagn P og operator forbundet med eller operatør til at danne en sammensat erklæring er skrevet som:
\large{p \vee.}.
{p \vee}} læses som “p Eller..”
husk: sandhedsværdien af den sammensatte sætning P \vee.er sand, hvis sandhedsværdien af enten de to enkle udsagn P og. er sand., Moreso, P \ vee Q er også sandt, når sandhedsværdierne for begge udsagn P og Q er sande. Men den eneste gang disjunction-erklæringen p \ vee V er falsk, sker, når sandhedsværdierne for både P og V er falske.
IV. Sandhedstabel for Logisk Konsekvens
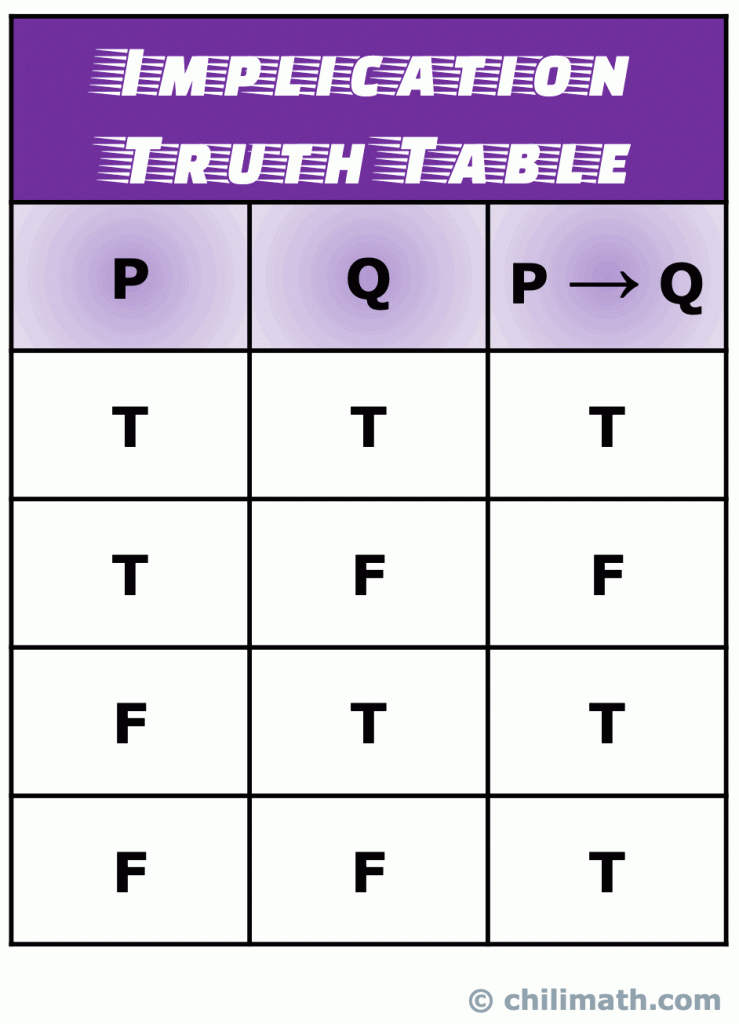
En implikation (også kendt som en betinget sætning) er en type af sammensatte udsagn, der er dannet ved at deltage i to simple sætninger med logisk konsekvens bindevæv eller operatør.,
symbolet, der bruges til at repræsentere den logiske implikationsoperatør, er en pil, der peger til højre, således en højre pil.

Når to enkle udsagn P og Q er gået, og de konsekvenser, operatør, har vi:
\Large{P \Q}.
- hvor P er kendt som hypotesen
- hvor conclusion er kendt som konklusionen
Der er mange måder, hvordan man læser den betingede {p \til}}., Nedenfor er nogle af de få almindelige.
husk: sandhedsværdien af den sammensatte sætning p \til to er sand, når både de enkle udsagn P og.er sande. Moreso, p \til Q er altid sandt, hvis P er falsk. Det eneste scenario, at p \til Q er falsk, sker, når P er sandt, og Q er falsk.
V., Sandhedstabel med logisk Bibetinget eller dobbelt implikation
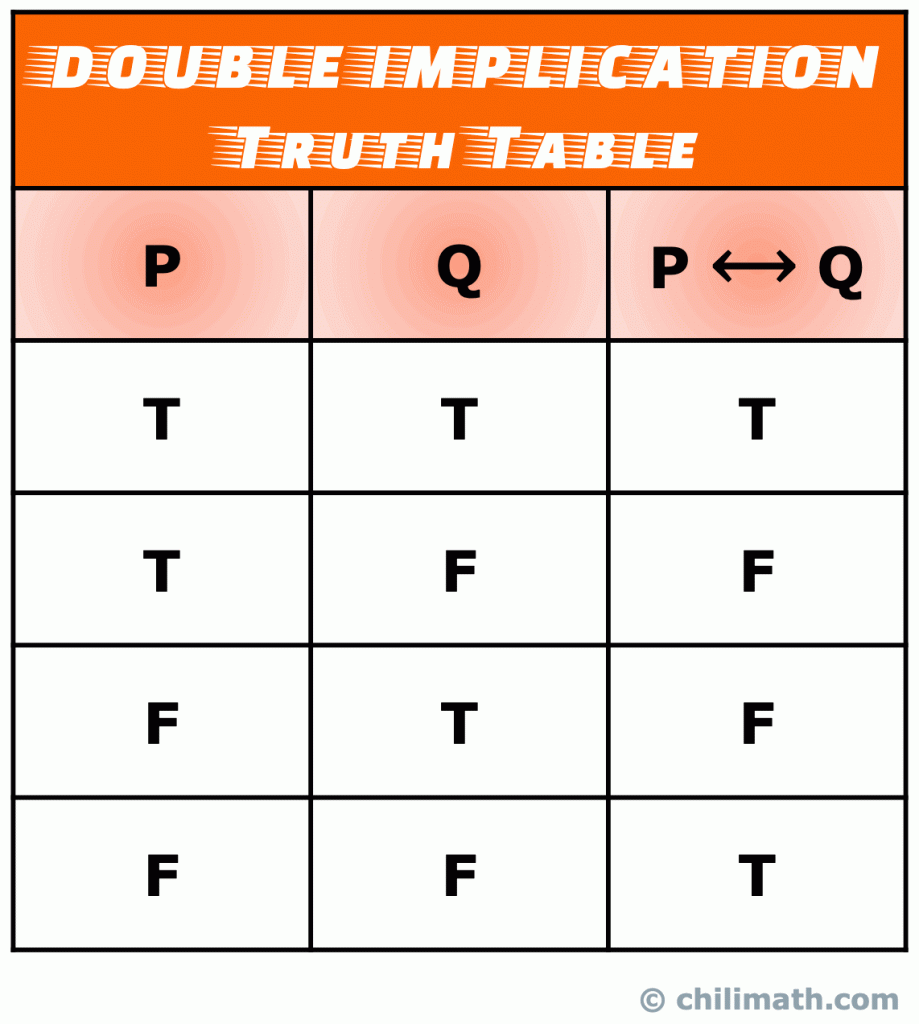
en dobbelt implikation (også kendt som en bibetinget erklæring) er en type sammensat erklæring, der dannes ved at forbinde to enkle udsagn med den bibetingede operatør. En bibetinget erklæring er virkelig en kombination af en betinget erklæring og dens omvendelse.
den bikonditionelle operatør betegnes med en dobbelthovedet pil.,

Når du tilmelder dig to enkle udsagn (også kendt som molekylær-sætninger) med biconditional operatør, får vi:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} læses som “P, hvis og kun hvis Q.,”
- hvor P er kendt som antecedent
- hvor Q er kendt som den deraf følgende
Husk: sandheden værdi af biconditional erklæring S \leftrightarrow Q er sandt, når både enkle udsagn P og Q begge er sande eller begge er falske. Ellers er p \leftrightarro.Q falsk.
Du er måske også interesseret i:
Introduktion til Sandheden Tabeller, Udsagn og Logisk Connectives
Converse, Inverse, og Contrapositive af en Betinget Sætning
Skriv et svar