El determinante de una matriz es un número especial que se puede calcular a partir de una matriz cuadrada.
Una Matriz es un array de números:
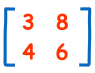
Una Matriz
(Este tiene 2 Filas y 2 Columnas)
El determinante de dicha matriz es (los cálculos se explican más adelante):
¿Qué es?
El determinante nos ayuda a encontrar la inversa de una matriz, nos dice cosas sobre la matriz que son útiles en sistemas de ecuaciones lineales, cálculo y más.,
símbolo
el símbolo para determinante es dos líneas verticales a cada lado.
Ejemplo:<|p>
/ A / significa el determinante de la matriz a
(exactamente el mismo símbolo que el valor absoluto.)
calcular el determinante
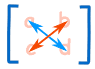
En primer lugar, la matriz debe ser cuadrada (es decir, tener el mismo número de filas que las columnas). Entonces es sólo aritmética básica., remember when you think of a cross:
- Blue is positive (+ad),
- Red is negative (−bc)
Example:
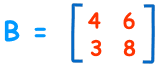
For a 3×3 Matrix
For a 3×3 matrix (3 rows and 3 columns):
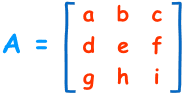
The determinant is:
|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
«The determinant of A equals .,.. etc »
Puede parecer complicado, pero hay un patrón:
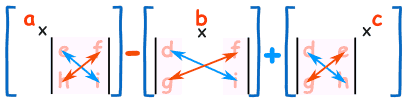
para calcular el determinante de una matriz 3×3:
- multiplique a por el determinante de la matriz 2×2 que no está en la fila o columna de a.
- Lo mismo para b, y para c
- sumarlos, pero recuerde el menos delante de la b
<| ul>
como una fórmula (recuerde las barras verticales | /significan «determinante de»):
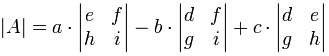
«El determinante de A es igual a a veces el determinante de …,
Para 4×4 Matrices y Superior
El patrón que se sigue para la 4×4 matrices:
- más veces el determinante de la matriz que no está en una fila o columna,
- minus b veces el determinante de la matriz que no está en b, fila o columna,
- c veces el determinante de la matriz que no es en c, fila o columna,
- menos d veces el determinante de la matriz que no es en d de la fila o columna,

Como una fórmula:
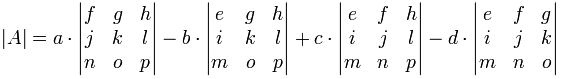
Observe el +−+− patrón (+a.,.. – b… + C… – d…). Es importante recordar esto.
el patrón continúa para matrices de 5×5 y superiores. Por lo general, lo mejor es utilizar una calculadora de matriz para los!
No es La Única Forma
Este método de cálculo se llama la «expansión de Laplace» y me gusta porque el patrón es fácil de recordar. Pero hay otros métodos (solo para que lo sepas).,
resumen
- Para una matriz 2×2 el determinante es ad – BC
- Para una matriz 3×3 multiplicar a por el determinante de la matriz 2×2 que no está en la fila o columna de a, lo mismo para b y c, pero recuerde que b tiene un signo negativo!
- El patrón continúa para matrices más grandes: multiplique a por el determinante de la matriz que no está en la fila o columna de a, continúe así en toda la fila, pero recuerde el patrón+−+−.
Deja una respuesta