el Teorema de Pitágoras

Una de las fórmulas matemáticas más conocidas es el Teorema de Pitágoras, que nos proporciona la relación entre los lados en un triángulo rectángulo. Un triángulo rectángulo consiste en dos piernas y una hipotenusa. Las dos patas se encuentran en un ángulo de 90° y la hipotenusa es el lado más largo del triángulo rectángulo y es el lado opuesto al ángulo recto.,

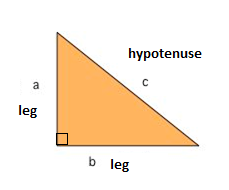
El Teorema de Pitágoras nos dice que la relación en cada triángulo rectángulo es:

$$a^{2}+b^{2}=c^{2}$$

Ejemplo

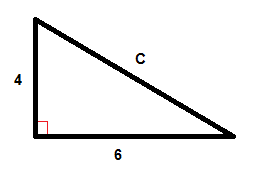
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\aprox 7.2$$

Hay un par de tipos especiales de los triángulos rectángulos, como el de 45°-45° a la derecha triángulos y los 30°-60° a la derecha del triángulo.,

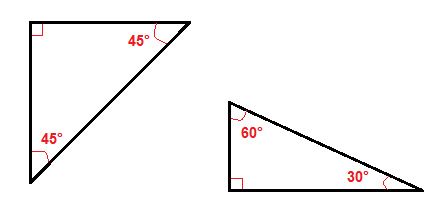
debido a sus ángulos, es más fácil encontrar la hipotenusa o las piernas en estos triángulos rectángulos que en todos los demás triángulos rectángulos.

en un triángulo rectángulo de 45°-45° solo necesitamos multiplicar una pierna por √2 para obtener la longitud de la hipotenusa.

Ejemplo

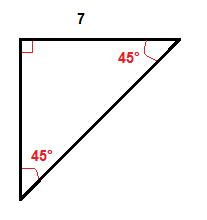
multiplicamos la longitud de la pierna, que es de 7 pulgadas por √2 para obtener la longitud de la hipotenusa.

7 7\cdot \sqrt {2}\approx 9.,9 <

en un triángulo rectángulo de 30°-60° podemos encontrar la longitud de la pierna que está opuesta al ángulo de 30° usando esta fórmula:

a A=\frac{1}{2}\cdot C example

ejemplo

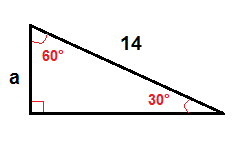
para encontrar a, usamos la fórmula anterior.

$$a=\frac{1}{2}\cdot 14$$

$$a=7$$

lección de Vídeo

Encontrar los lados de este triángulo rectángulo