vista general
- Los inconvenientes de las estadísticas frecuentistas conducen a la necesidad de estadísticas Bayesianas
- descubrir estadísticas Bayesianas e inferencia bayesiana
- Hay varios métodos para probar la importancia del modelo como valor p, intervalo de confianza, etc
Introducción
las estadísticas bayesianas siguen siendo incomprensibles en las mentes encendidas de muchos analistas., Sorprendidos por el increíble poder del aprendizaje automático, muchos de nosotros nos hemos vuelto infieles a las estadísticas. Nuestro enfoque se ha reducido a explorar el aprendizaje automático. ¿No es verdad?
no entendemos que el aprendizaje automático no es la única manera de resolver problemas del mundo real. En varias situaciones, no nos ayuda a resolver problemas de negocio, a pesar de que hay datos involucrados en estos problemas. Por decir lo menos, el conocimiento de las estadísticas le permitirá trabajar en problemas analíticos complejos, independientemente del tamaño de los datos.,
en la década de 1770, Thomas Bayes introdujo el Teorema de Bayes. Incluso después de siglos más tarde, la importancia de las’ estadísticas Bayesianas ‘ no se ha desvanecido. De hecho, hoy en día este tema se enseña en gran profundidad en algunas de las principales universidades del mundo.
con esta idea, he creado esta guía para principiantes sobre estadísticas Bayesianas. He tratado de explicar los conceptos de una manera simplista con ejemplos. Es deseable un conocimiento previo de las estadísticas básicas de probabilidad &., Usted debe comprobar hacia fuera este curso para conseguir un bajo comprensivo abajo en estadísticas y probabilidad.
al final de este artículo, tendrá una comprensión concreta de las estadísticas Bayesianas y sus conceptos asociados.,>Teorema de Bayes
- Función de verosimilitud de Bernoulli
- Distribución de creencias anterior
- Distribución de creencias Posterior
- Valor p
- intervalos de confianza
- Factor de Bayes
- intervalo de alta densidad (HDI)
antes de profundizar en las estadísticas bayesianas, pasemos unos minutos entendiendo las estadísticas Frecuentistas, la versión más popular de las estadísticas que la mayoría de nosotros encontramos y los problemas inherentes en eso.,
estadísticas de Frecuentistas
el debate entre frecuentistas y bayesianos ha perseguido a los principiantes durante siglos. Por lo tanto, es importante entender la diferencia entre los dos y cómo existe una delgada línea de demarcación!
es la técnica inferencial más utilizada en el mundo estadístico. De hecho, generalmente es la primera escuela de pensamiento que una persona que entra en el mundo de las estadísticas se encuentra.
las estadísticas de Frecuentistas prueban si un evento (hipótesis) ocurre o no., Calcula la probabilidad de un evento en el largo plazo del experimento (es decir, el experimento se repite en las mismas condiciones para obtener el resultado).
aquí se toman las distribuciones de muestreo de tamaño fijo. Luego, el experimento se repite teóricamente un número infinito de veces, pero prácticamente se realiza con una intención de detención. Por ejemplo, realizo un experimento con una intención de detener en mente que detendré el experimento cuando se repite 1000 veces o veo un mínimo de 300 cabezas en un lanzamiento de moneda.
Vamos a profundizar ahora.,
ahora, entenderemos las estadísticas de frecuentistas usando un ejemplo de lanzamiento de moneda. El objetivo es estimar la equidad de la moneda. A continuación se muestra una tabla que representa la frecuencia de las cabezas:

sabemos que la probabilidad de obtener una cabeza al lanzar una moneda justa es 0.5. No. of heads representa el número real de cabezas obtenidas. Difference es la diferencia entre 0.5*(No. of tosses) - no. of heads.,
una cosa importante es tener en cuenta que, aunque la diferencia entre el número real de cabezas y el número esperado de cabezas( 50% del número de lanzamientos) aumenta a medida que aumenta el número de lanzamientos, la proporción del número de cabezas en el número total de lanzamientos se acerca a 0.5 (para una moneda justa).
este experimento nos presenta un defecto muy común que se encuentra en el enfoque frecuentista, es decir, la dependencia del resultado de un experimento en el número de veces que el experimento se repite.,
para saber más sobre los métodos estadísticos frecuentistas, puede dirigirse a este excelente curso sobre estadísticas inferenciales.
Los Defectos Inherentes en Frecuentista Estadísticas
Hasta aquí, hemos visto sólo un defecto en la estadística frecuentista. Bueno, es sólo el principio.
el siglo XX vio un aumento masivo en las estadísticas frecuentistas que se aplican a los modelos numéricos para verificar si una muestra es diferente de la otra, un parámetro es lo suficientemente importante como para mantenerse en el modelo y varias otras manifestaciones de pruebas de hipótesis., Pero las estadísticas frecuentistas sufrieron algunas grandes fallas en su diseño e interpretación que plantearon una seria preocupación en todos los problemas de la vida real. Por ejemplo:
p-values medido contra una estadística de muestra (tamaño fijo) Con algunos cambios de intención de detención con cambio en la intención y el tamaño de la muestra. es decir, si dos personas trabajan en los mismos datos y tienen una intención de detención diferente, pueden obtener dos p- values diferentes para los mismos datos, lo cual no es deseable.,
por ejemplo: la persona A puede optar por dejar de lanzar una moneda cuando el recuento total alcanza 100 mientras que B se detiene en 1000. Para diferentes tamaños de muestra, obtenemos diferentes puntuaciones t y diferentes valores P. Del mismo modo, la intención de detener puede cambiar de número fijo de giros a la duración total del giro. En este caso también, estamos obligados a obtener diferentes valores de P.
2 – Confidence Interval (C. I) like p-value depende en gran medida del tamaño de la muestra., Esto hace que el potencial de detención sea absolutamente absurdo, ya que no importa cuántas personas realicen las pruebas en los mismos datos, los resultados deben ser consistentes.
3 – Intervalos de Confianza (C. I) no son distribuciones de probabilidad, por tanto, no proporcionan la más probable de valor para un parámetro y los valores más probables.
estas tres razones son suficientes para que te pongas a pensar en los inconvenientes del enfoque frecuentista y por qué hay una necesidad de enfoque bayesiano. Vamos a averiguarlo.,
a partir de aquí, primero entenderemos los fundamentos de las estadísticas Bayesianas.
Bayesian Statistics
» Bayesian statistics is a mathematical procedure that applies probabilities to statistical problems. Proporciona a las personas las herramientas para actualizar sus creencias en la evidencia de nuevos datos.»
¿lo tienes? Permítanme explicarlo con un ejemplo:
supongamos que, de todas las 4 carreras de campeonato (F1) entre Niki Lauda y James hunt, Niki ganó 3 veces mientras que James logró solo 1.,
entonces, si apostaras por el ganador de la próxima carrera, ¿quién sería?
apuesto a que dirías Niki Lauda.
Aquí está el giro. ¿Qué pasa si te dicen que llovió una vez cuando James ganó y una vez cuando Niki ganó y es definitivo que lloverá en la próxima fecha. Entonces, ¿por quién apostarías tu dinero ahora ?
por intuición, es fácil ver que las posibilidades de ganar para James han aumentado drásticamente. Pero la pregunta es: ¿cuánto ?,
para entender el problema en cuestión, necesitamos familiarizarnos con algunos conceptos, el primero de los cuales es la probabilidad condicional (explicada a continuación).
además, hay ciertos pre-requisitos:
Pre-requisitos:
- Álgebra Lineal : para actualizar tus conceptos básicos, puedes consultar el álgebra de Khan Academy.
- Probabilidad y estadísticas básicas: para actualizar tus conocimientos básicos, puedes consultar otro curso de Khan Academy.
3.,1 probabilidad condicional
se define como: la probabilidad de un evento a dado B es igual a la probabilidad de que B y A sucedan juntos divididos por la probabilidad de B.»
Por ejemplo: asumir dos conjuntos parcialmente intersecados A y B como se muestra a continuación.
el conjunto A representa un conjunto de eventos y el conjunto B representa otro. Queremos calcular la probabilidad de que una B dada ya haya sucedido. Vamos a representar el acontecimiento del evento B sombreándolo con rojo.,
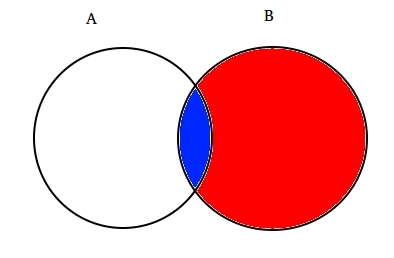
Ahora, dado que B ha ocurrido, la parte que ahora importa por que es la parte sombreada en azul, que es curiosamente ![]() . Así, la probabilidad de a dado B resulta ser:
. Así, la probabilidad de a dado B resulta ser:
por lo Tanto, podemos escribir la fórmula para el evento B dado que ya se produjo por:
o
Ahora, la segunda ecuación se puede reescribir como :
Esto es conocido como la Probabilidad Condicional.,
intentemos resolver un problema de apuestas con esta técnica.
supongamos, B ser el evento de ganar de James Hunt. A ser el evento de la lluvia. Por lo tanto,
sustituyendo los valores en la fórmula de probabilidad condicional, obtenemos la probabilidad de estar alrededor del 50%, que es casi el doble de 25% cuando no se tuvo en cuenta la lluvia (Soluciónelo al final).
esto fortaleció aún más nuestra creencia de que James ganó a la luz de las nuevas pruebas, es decir, la lluvia., Usted debe estar preguntándose que esta fórmula se parece mucho a algo que usted podría haber oído hablar mucho. Piensa!
probablemente, lo adivinaste bien. Parece el Teorema de Bayes.
El teorema de Bayes está construido sobre la probabilidad condicional y se encuentra en el corazón de la inferencia bayesiana. Vamos a entenderlo en detalle ahora.
3.2 Teorema de Bayes
El teorema de Bayes entra en vigor cuando múltiples eventos forman un conjunto exhaustivo con otro evento B. Esto podría entenderse con la ayuda del siguiente diagrama.,

Ahora, B puede ser escrito como
Así, la probabilidad de que B se puede escribir como,
Pero![]()
Así, reemplazando P(B) en la ecuación de la probabilidad condicional obtenemos

Esta es la ecuación del Teorema de Bayes.
inferencia bayesiana
no tiene sentido sumergirse en el aspecto teórico de la misma. Por lo tanto, vamos a aprender cómo funciona!, Tomemos un ejemplo de lanzamiento de monedas para entender la idea detrás de la inferencia bayesiana.
Una parte importante de la inferencia bayesiana es el establecimiento de parámetros y modelos.
Modelos son la formulación matemática de los eventos observados. Los parámetros son los factores de los modelos que afectan a los datos observados. Por ejemplo, al lanzar una moneda, la equidad de la moneda puede definirse como el parámetro de la moneda denotado por θ. El resultado de los eventos puede ser denotado por D.
conteste esto ahora., Cuál es la probabilidad de 4 cabezas de 9 lanzamientos (D) dada la equidad de la moneda (θ). es decir, P(D|θ)
espere, ¿hice la pregunta correcta? No.
deberíamos estar más interesados en saber : dado un resultado (D) Cuál es la probabilidad de que la moneda sea justa (θ=0.5)
vamos a representarla usando el Teorema de Bayes:
P(θ|D)=(P(D|θ) X P(θ))/P(D)
aquí, P(θ) es el anterior, es decir, la fuerza de nuestra creencia en la equidad de la moneda antes del lanzamiento., Está perfectamente bien creer que la moneda puede tener cualquier grado de equidad entre 0 y 1.
P(D|θ) es la probabilidad de observar nuestro resultado de nuestra distribución para θ. Si supiéramos que la moneda era justa, esto da la probabilidad de observar el número de cabezas en un número particular de giros.
P(D) es la evidencia. Esta es la probabilidad de datos determinada sumando (o integrando) a través de todos los valores posibles de θ, ponderada por cuán fuertemente creemos en esos valores particulares de θ.,
si tuviéramos múltiples puntos de vista de lo que es la equidad de la moneda (pero no lo sabíamos con certeza), entonces esto nos dice la probabilidad de ver una cierta secuencia de giros para todas las posibilidades de nuestra creencia en la equidad de la moneda.
P(θ|D) es la creencia posterior de nuestros parámetros después de observar la evidencia, es decir, el número de cabezas .
desde aquí, profundizaremos en las implicaciones matemáticas de este concepto. No te preocupes. Una vez que los entiendes, llegar a sus matemáticas es bastante fácil.,
para definir nuestro modelo correctamente, necesitamos dos modelos matemáticos antes de la mano. Una para representar la función de verosimilitud P (D / θ) y la otra para representar la distribución de creencias previas . El producto de estos dos da la creencia posterior p(θ|D) distribución.
dado que tanto anterior como posterior son creencias sobre la distribución de la equidad de la moneda, la intuición nos dice que ambas deben tener la misma forma matemática. Ten esto en mente. Volveremos a ello de nuevo.,
por lo tanto, hay varias funciones que apoyan la existencia del teorema de bayes. Conocerlos es importante, por lo tanto, los he explicado en detalle.
4.1. Función de verosimilitud de Bernoulli
recapitulemos lo que aprendimos sobre la función de verosimilitud. Por lo tanto, aprendimos que:
es la probabilidad de observar un número particular de cabezas en un número particular de giros para una equidad dada de la moneda. Esto significa que nuestra probabilidad de observar cara/cruz depende de la equidad de la moneda (θ).,
P(y=1|θ)=
P(y=0|θ)=
cabe hacer notar que representa el 1 como jefes y 0 como colas es sólo una notación matemática para formular un modelo. Podemos combinar las definiciones matemáticas anteriores en una sola definición para representar la probabilidad de ambos resultados.
P(y/θ)=
esto se llama la función de verosimilitud de Bernoulli y la tarea de voltear monedas se llama ensayos de Bernoulli.,
y={0,1},θ=(0,1)
Y, cuando queremos ver una serie de jefes o volteretas, su probabilidad está dada por:
Además, si estamos interesados en la probabilidad de que el número de cabezas de z de inflexión en N número de lanzamientos, la probabilidad está dada por:
4.2. Distribución de creencias anteriores
esta distribución se utiliza para representar nuestras fortalezas en creencias sobre los parámetros basados en la experiencia previa.,
pero, ¿qué pasa si uno no tiene experiencia previa?
no te preocupes. Los matemáticos también han ideado métodos para mitigar este problema. Se conoce como uninformative priors. Me gustaría informarles de antemano que es un nombre equivocado. Cada previo desinformativo siempre proporciona algún evento de información el previo de distribución constante.
Así, la función matemática utilizada para representar las creencias anteriores se conoce como beta distribution., Tiene algunas propiedades matemáticas muy buenas que nos permiten modelar nuestras creencias sobre una distribución binomial.
La función de densidad de probabilidad de la distribución beta es de la forma:
donde, nuestro enfoque se mantiene en numerador. El denominador está ahí solo para asegurar que la función de densidad de probabilidad total sobre la integración evalúa a 1.
α and β are called the shape deciding parameters of the density function., Aquí α es análogo al número de cabezas en las pruebas y β corresponde al número de colas., Los diagramas a continuación le ayudarán a visualizar las distribuciones beta para diferentes valores de α y β

usted también puede dibujar la distribución beta por sí mismo utilizando el siguiente código en R:
nota: α y β son intuitivos de entender ya que se pueden calcular conociendo la media (μ) y la desviación estándar (σ) de la distribución., De hecho, están relacionados como:
Si se conocen la media y la desviación estándar de una distribución , entonces los parámetros de forma se pueden calcular fácilmente.
inferencia extraída de los gráficos anteriores:
- Cuando no hubo lanzamiento, creímos que cada equidad de la moneda es posible según lo representado por la línea plana.
- cuando había más número de cabezas que las colas, el gráfico mostró un pico desplazado hacia el lado derecho, lo que indica una mayor probabilidad de cabezas y que la moneda no es justa.,
- a medida que se realizan más lanzamientos, y las cabezas continúan llegando en mayor proporción, el pico se estrecha aumentando nuestra confianza en la equidad del valor de la moneda.
4.3. Distribución de creencia Posterior
la razón por la que elegimos creencia anterior es para obtener una distribución beta. Esto se debe a que cuando lo multiplicamos con una función de verosimilitud, la distribución posterior produce una forma similar a la distribución anterior que es mucho más fácil de relacionar y entender., Si tanta información te abre el apetito, estoy seguro de que estás listo para caminar un poco más.
calculemos la creencia posterior usando el teorema de bayes.
el Cálculo posterior de la creencia utilizando el Teorema de Bayes,
Ahora, nuestra posterior de la creencia se convierte,
Esto es interesante., Simplemente conociendo la distribución media y estándar de nuestra creencia sobre el parámetro θ y observando el número de cabezas en n volteos, podemos actualizar nuestra creencia sobre el parámetro del modelo(θ).
vamos a entender esto con la ayuda de un simple ejemplo:
supongamos que usted piensa que una moneda está sesgada. Tiene un sesgo medio (μ) de alrededor de 0.6 con desviación estándar de 0.1.
Entonces
α= 13.8 , β=9.2
i.,e nuestra distribución estará sesgada en el lado derecho. Supongamos que ha observado 80 cabezas (z=80) en 100 volteretas(N=100). Vamos a ver cómo nuestro previo y posterior de las creencias van a buscar:
prior = P(θ|α,β)=P(θ|13.8,9.2)
Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)
Permite visualizar tanto las creencias en un gráfico:

El código R para el gráfico anterior es:
}
a Medida que más y más saltos se realizan y los nuevos datos se observa, nuestras creencias se actualiza., Este es el verdadero poder de la inferencia bayesiana.
Test for Significance – Frequentist vs Bayesian
sin entrar en las estructuras matemáticas rigurosas, esta sección le proporcionará una visión rápida de los diferentes enfoques de los métodos frecuentistas y bayesianos para probar la significación y la diferencia entre los grupos y qué método es más confiable.
5.1. p-value
en esto, se calcula la puntuación t para una muestra particular de una distribución de muestreo de tamaño fijo. Entonces, se predicen los valores de P., Podemos interpretar los valores de p como (tomando un ejemplo de valor de p como 0.02 para una distribución de media 100): hay un 2% de probabilidad de que la muestra tenga Media igual a 100.
esta interpretación sufre el defecto de que para distribuciones de muestreo de diferentes tamaños, uno está obligado a obtener diferentes t-score y por lo tanto diferentes p-valor. Es completamente absurdo. Un valor de p inferior al 5% no garantiza que la hipótesis nula sea incorrecta ni un valor de p superior al 5% garantiza que la hipótesis nula sea correcta.
5.2., Los intervalos de confianza
los intervalos de confianza también sufren del mismo defecto. Además, dado que C. I no es una distribución de probabilidad , no hay forma de saber qué valores son más probables.
5.3. Factor Bayes
el factor Bayes es el equivalente del valor p en el marco bayesiano. Vamos a entenderlo de una manera integral.
la hipótesis nula en el marco bayesiano asume la distribución de probabilidad ∞ solo en un valor particular de un parámetro (digamos θ=0.5) y una probabilidad cero en otro lugar., (M1)
la hipótesis alternativa es que todos los valores de θ son posibles, por lo tanto una curva plana que representa la distribución. (M2)
ahora, la distribución posterior de los nuevos datos se ve como a continuación.

estadística Bayesiana ajustada credibilidad (probabilidad) de varios valores de θ. Se puede ver fácilmente que la distribución de probabilidad se ha desplazado hacia M2 con un valor superior a M1, es decir, M2 es más probable que suceda.,
el factor de Bayes no depende de los valores de distribución reales de θ sino de la magnitud del cambio en los valores de M1 y M2.
en el panel a (mostrado arriba): la barra izquierda (M1) es la probabilidad previa de la hipótesis nula.
en el panel B (mostrado), la barra izquierda es la probabilidad posterior de la hipótesis nula.
el factor de Bayes se define como la relación de las odds posteriores a las odds anteriores,
Para rechazar una hipótesis nula, se prefiere un BF <1/10.,
podemos ver los beneficios inmediatos de usar el factor Bayes en lugar de los valores p, ya que son independientes de las intenciones y el tamaño de la muestra.
5.4. Intervalo de alta densidad (HDI)
el HDI se forma a partir de la distribución posterior después de observar los nuevos datos. Dado que el IDH es una probabilidad, el IDH del 95% da el 95% de los valores más creíbles. También se garantiza que los valores del 95% estarán en este intervalo a diferencia de C. I.
observe cómo el IDH del 95% en la distribución anterior es más amplio que la distribución posterior del 95%., Esto se debe a que nuestra creencia en el IDH aumenta al observar nuevos datos.

notas finales
el objetivo de este artículo era hacerte pensar sobre los diferentes tipos de filosofías estadísticas que existen y cómo ninguna de ellas puede usarse en cada situación.
ya es hora de que ambas filosofías se fusionen para mitigar los problemas del mundo real abordando los defectos del otro., La Parte II de esta serie se centrará en las técnicas de reducción de dimensionalidad utilizando algoritmos MCMC (Markov Chain Monte Carlo). La Parte III se basará en crear un modelo de regresión Bayesiana desde cero e interpretar sus resultados en R. así que, antes de comenzar con la Parte II, Me gustaría tener sus sugerencias / comentarios sobre este artículo.
Deja una respuesta