|
«Bi» significa «dos» (como una bicicleta tiene dos ruedas) … |
 |

Lanzar una Moneda:
- llegamos Cabezas (H) o
- Colas (T)
Nos dicen que la probabilidad de que la moneda caiga de H es de ½
Y la probabilidad de que la moneda caiga de T de ½
Vamos a Tirar una Moneda al aire!
lanza una moneda justa tres veces … ¿Cuál es la posibilidad de conseguir dos cabezas?,tr>












Which outcomes do we want?,
«dos cabezas» podría estar en cualquier orden: «HHT», «THH» y » HTH » todos tienen dos cabezas (y una cola).
así que 3 de los resultados producen «dos cabezas».
¿Cuál es la probabilidad de cada resultado?,aciones son (P significa «Probabilidad»):
- P(Tres Cabezas) = P(HHH) = 1/8
- P(Dos Caras) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Una Cabeza) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Cero Cabezas) = P(TTT) = 1/8
podemos escribir esto en términos de una Variable Aleatoria, X, = «El número de Cabezas de 3 lanzamientos de una moneda»:
- P(X = 3) = 1/8
- P(X = 2) = 3/8
- P(X = 1) = 3/8
- P(X = 0) = 1/8
Y esto es lo que se ve como un gráfico:
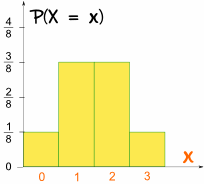
es simétrico!,
hacer una fórmula
ahora imagine que queremos las posibilidades de 5 cabezas en 9 lanzamientos: para enumerar todos los 512 resultados tomará mucho tiempo!
así que vamos a hacer una fórmula.
En nuestro ejemplo anterior, ¿cómo podemos obtener los valores 1, 3, 3 y 1 ?
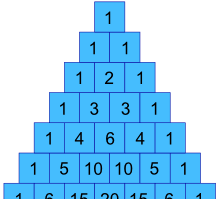
Bueno, en realidad están en el Triángulo de Pascal !
¿Podemos hacerlos usando una fórmula?
Asegúrese de que podemos, y aquí es:
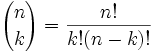
es a menudo llamado «n elegir k»
- n = número total
- k = número queremos
- «!,»significa » factorial», por ejemplo 4! = 1×2×3×4 = 24
puedes leer más sobre ello en combinaciones y permutaciones.
probémoslo:
usémoslo para una pregunta más difícil:
¡sesgo!
hasta ahora las posibilidades de éxito o fracaso han sido igualmente probables.
pero qué pasa si las monedas están sesgadas (la tierra más en un lado que en otro) o las opciones no son 50/50.
ejemplo: vendes sándwiches. El 70% de la gente elige pollo, el resto elige otra cosa.
esto es igual que el ejemplo de cara y Cruz, pero con 70/30 en lugar de 50/50.,
Vamos a dibujar un diagrama de árbol:
Los Dos «Pollo» de los casos se destacan.
todas las probabilidades para «dos pollos» resultan ser 0.147, porque estamos multiplicando dos 0.7 s y uno 0.3 en cada caso. En otras palabras
0.147 = 0.7 × 0.7 × 0.3
O, utilizando los exponentes:
= 0.72 × 0.31
El 0,7 es la probabilidad de cada una de las opciones que queremos, llamamos p
El 2 es el número de opciones que desea, llame a k
Y tenemos (por ahora):
= pk × 0.31
El 0.,3 es la probabilidad de que la elección opuesta, por lo que es: 1−p
el 1 es El número de enfrente de opciones, por lo que es: n−k
lo Que nos da:
= pk(1-p)(n-k)
Donde
- p es la probabilidad de cada una de las opciones que queremos
- k es el número de opciones que queremos
- n es el número total de opciones
Ahora que sabemos que la probabilidad de cada resultado es 0.147
ACEPTAR. Eso fue mucho trabajo para algo que ya sabíamos, pero ahora tenemos una fórmula que podemos usar para preguntas más difíciles.,
Poner Juntos
Ahora sabemos cómo calcular la cantidad:
n!¡k!(n-k)!
Y la probabilidad de cada uno de ellos:
pk(1-p)(n-k)
Cuando se multiplican juntos obtenemos:
Probabilidad de que k de n maneras:
P(k de n) = n!¡k!(n-k)! pk(1-p) (n-k)
la fórmula general de probabilidad Binomial
notas importantes:
- Los ensayos son independientes,
- solo hay dos resultados posibles en cada ensayo,
- La probabilidad de «éxito» en cada ensayo es constante.,
Tresbolillo

Tener un juego con el Tresbolillo (luego de leer Tresbolillo Explicado) para ver la Distribución Binomial en la acción.
Lanzar el dado
Una feria de morir se produce cuatro veces. Calcule las probabilidades de obtener:
- 0 doses
- 1 Two
- 2 doses
- 3 doses
- 4 doses
en este caso n=4, p = P(dos) = 1/6
X es la Variable aleatoria ‘número de doses de cuatro tiros’.,
sustituya x = 0 a 4 en la fórmula:
P(k de n) = n!¡k!(n-k)! pk(1-p)(n-k)
Como este (4 decimales):
Esta vez la gráfica no es simétrica:
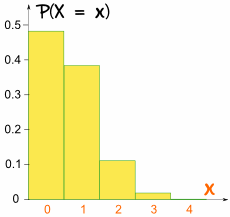
no es simétrico!
es sesgada porque p no es de 0,5

Motos Deportivas
Su empresa hace que las motos deportivas. El 90% pasa la inspección final (y el 10% falla y debe arreglarse).
¿Cuál es la media esperada y la varianza de las 4 próximas inspecciones?
primero, calculemos todas las probabilidades.,
- n = 4,
- p = P(Aprobar) = 0.9
X es la Variable Aleatoria «Número de pases de cuatro inspecciones».
sustituya x = 0 a 4 en la fórmula:
P(k de n) = n!¡k!(n-k)! pk(1-p) (n-k)
media, varianza y desviación estándar
calculemos la media, varianza y desviación estándar para las inspecciones de bicicletas deportivas.
hay fórmulas (relativamente) simples para ellos. Son un poco difíciles de probar, pero funcionan!,
La media, o de «valor esperado», es:
µ = np
La fórmula para la Varianza es:
la Varianza: σ2 = np(1-p)
Y la Desviación Estándar es la raíz cuadrada de la varianza:
σ = √(np(1-p))
Para las motos deportivas:
la Varianza: σ2 = 4 × 0.9 × 0.1 = 0.36
la Desviación Estándar es:
σ = √(0.36) = 0.6


Deja una respuesta