en esta lección, vamos a construir los cinco (5) conectivos u operadores lógicos comunes. Se consideran conectivos lógicos comunes porque son muy populares, útiles y siempre se enseñan juntos.
antes de comenzar, le sugiero que revise mi otra lección en la que se muestra el enlace a continuación.
esta lección introductoria sobre tablas de verdad contiene conocimiento o información prerrequisitos que le ayudarán a comprender mejor el contenido de esta lección.,
Introduction to Truth Tables, Statements and Conectives
Le’s start by listing the five (5) common logical conectives.
los cinco (5) conectivos u operadores lógicos comunes
- negación lógica
- conjunción lógica (y)
- disyunción lógica (Inclusive OR)
- implicación lógica (condicional)
- bicondicional lógica (doble implicación)
I., Tabla de verdad de negación lógica
la negación de una declaración es también una declaración con un valor de verdad que es exactamente opuesto al de la declaración original. Por ejemplo, la negación de la declaración se escribe simbólicamente como
~\large{P} o \large{\neg P}.
~{P} o {\neg P} se lee como «not p.»
recuerde: el operador de negación denotado por el símbolo ~ o \neg toma el valor de verdad de la declaración original y luego muestra exactamente lo contrario de su valor de verdad., En otras palabras, la negación simplemente invierte el valor de verdad de una declaración dada. Por lo tanto, si la declaración P es verdadera, entonces el valor de verdad de su negación es falso. De la misma manera si P es falso el valor de verdad de su negación es verdadero.

II. Tabla de verdad de la Conjunción Lógica
Una conjunción es un tipo de compuesto declaración, que consta de dos proposiciones (también conocido como simples declaraciones) acompañado por el operador and.,
el símbolo que se usa para representar el operador de conjunción AND O lógica es \color{red}\Large {\wedge}. Parece una letra invertida V.
si tenemos dos sentencias simples P y Q, y queremos formar una sentencia compuesta unida por el operador AND, podemos escribirla como:
\large{P \wedge Q}.
{P \Wedge Q} se lee como «P y Q.»
recuerde: el valor de verdad de la declaración compuesta P \wedge Q solo es verdadero si los valores de verdad P y Q son ambos verdaderos., De lo contrario, P \ wedge Q Es false.
observe en la tabla de verdad que cuando P es verdadero y Q es verdadero, P \ wedge Q es verdadero. Sin embargo, las otras tres combinaciones de proposiciones P y Q son falsas.

III. Tabla de verdad de la Lógica de la Disyunción
Una disyunción es un tipo de compuesto declaración que se compone de dos declaraciones simples formadas por las declaraciones con el operador or.
en una declaración de disyunción, el uso de OR es inclusivo. Eso significa «uno o el otro» o ambos.,
el símbolo que se utiliza para representar el operador de disyunción lógica OR or es \color{red}\Large{ \vee }. Se asemeja a la letra V del alfabeto.
dos proposiciones P Y Q unidas por el operador OR para formar una declaración compuesta se escriben como:
\large{P \vee Q}.
{P \vee Q} se lee «P o Q.»
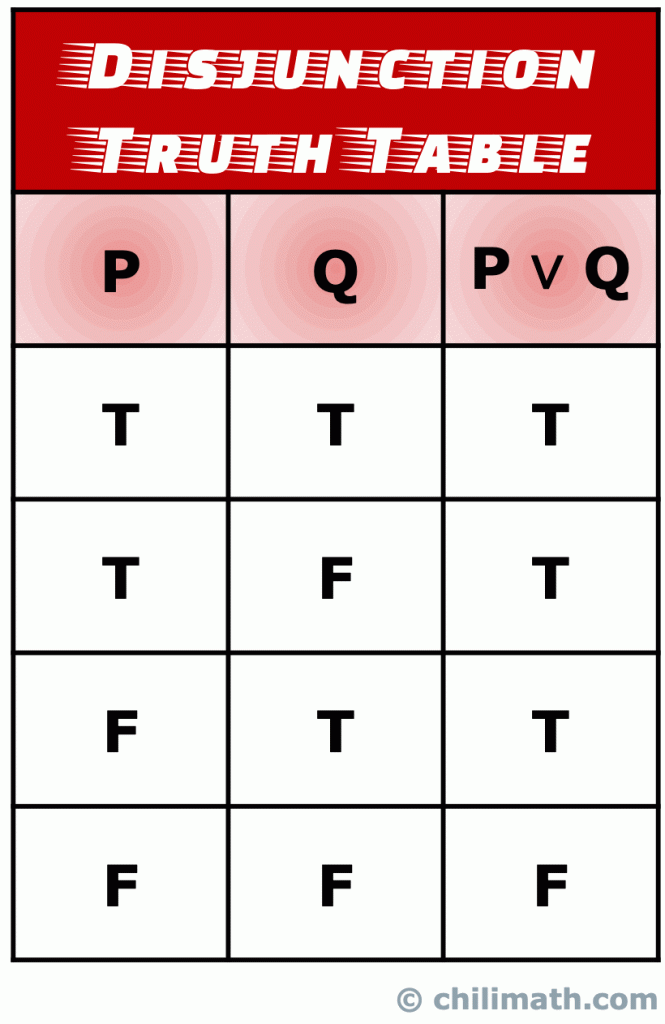
Recuerde: El valor de verdad de la instrucción compuesta P \vee Q es verdadera si el valor de verdad de las dos declaraciones simples P y Q es verdadera., Moreso, P \ vee Q también es verdadero cuando los valores de verdad de ambas declaraciones P y Q son verdaderos. Sin embargo, la única vez que la declaración de disyunción P \vee Q es falsa, ocurre cuando los valores de verdad de P y Q son falsos.
IV. Tabla de verdad de la Implicación Lógica
Una implicación (también conocido como una declaración condicional) es un tipo de instrucción compuesta, que está formado por la unión de dos simples declaraciones con la implicación lógica conectivo o de operador.,
el símbolo que se utiliza para representar el operador de implicación lógica es una flecha que apunta a la derecha, por lo tanto una flecha hacia la derecha.

Cuando dos declaraciones simples P y Q están unidas por el operador de implicación, tenemos:
\Large{P \Q}.
- donde P es conocida como la hipótesis
- donde Q es conocido como la conclusión
Hay muchas maneras de cómo leer el condicional {P \Q}., A continuación se presentan algunos de los pocos comunes.
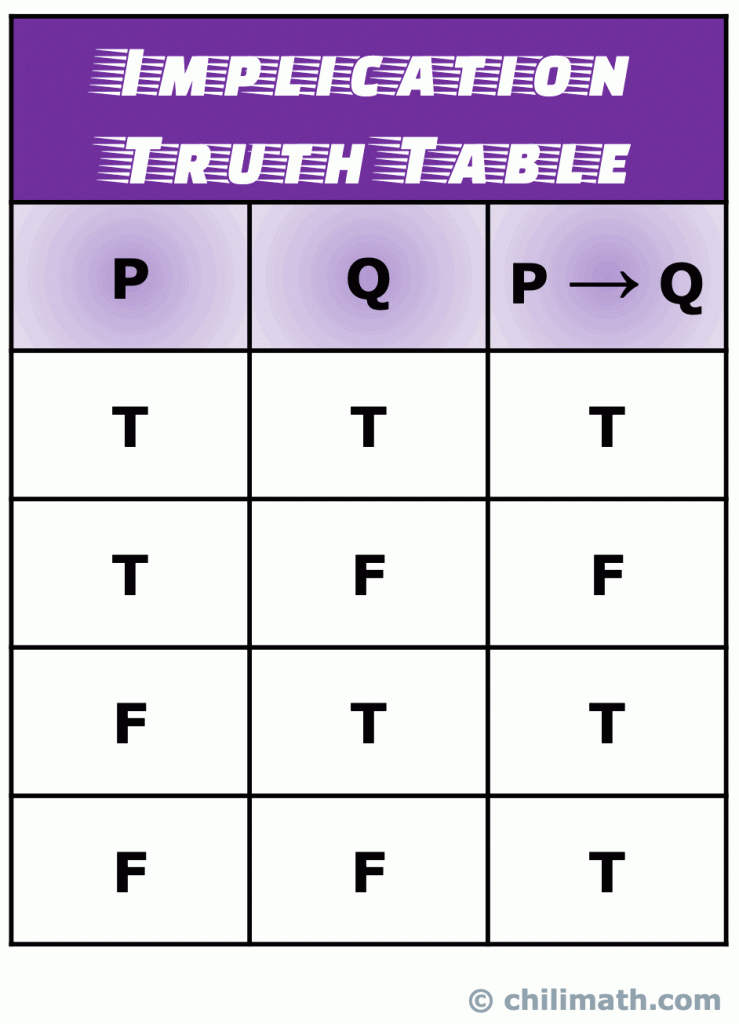
recuerde: el valor de verdad de la declaración compuesta P \ to Q es verdadero cuando las declaraciones simples p y Q son verdaderas. Además, P \to Q es siempre true si P es false. El único escenario que P \ A Q Es falso ocurre cuando P es verdadero, y Q es falso.
V., Tabla de verdad del bicondicional lógico o doble implicación
una doble implicación (también conocida como una declaración bicondicional) es un tipo de declaración compuesta que se forma al unir dos declaraciones simples con el operador bicondicional. Una declaración bicondicional es realmente una combinación de una declaración condicional y su conversa.
el operador bicondicional se denota por una flecha de dos cabezas.,

Cuando usted se une a dos simples declaraciones (también conocido como molecular declaraciones) con el bicondicional operador, obtenemos:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} se lee «P si y sólo si P.,»
- donde P se conoce como el antecedente
- Donde Q se conoce como el consecuente
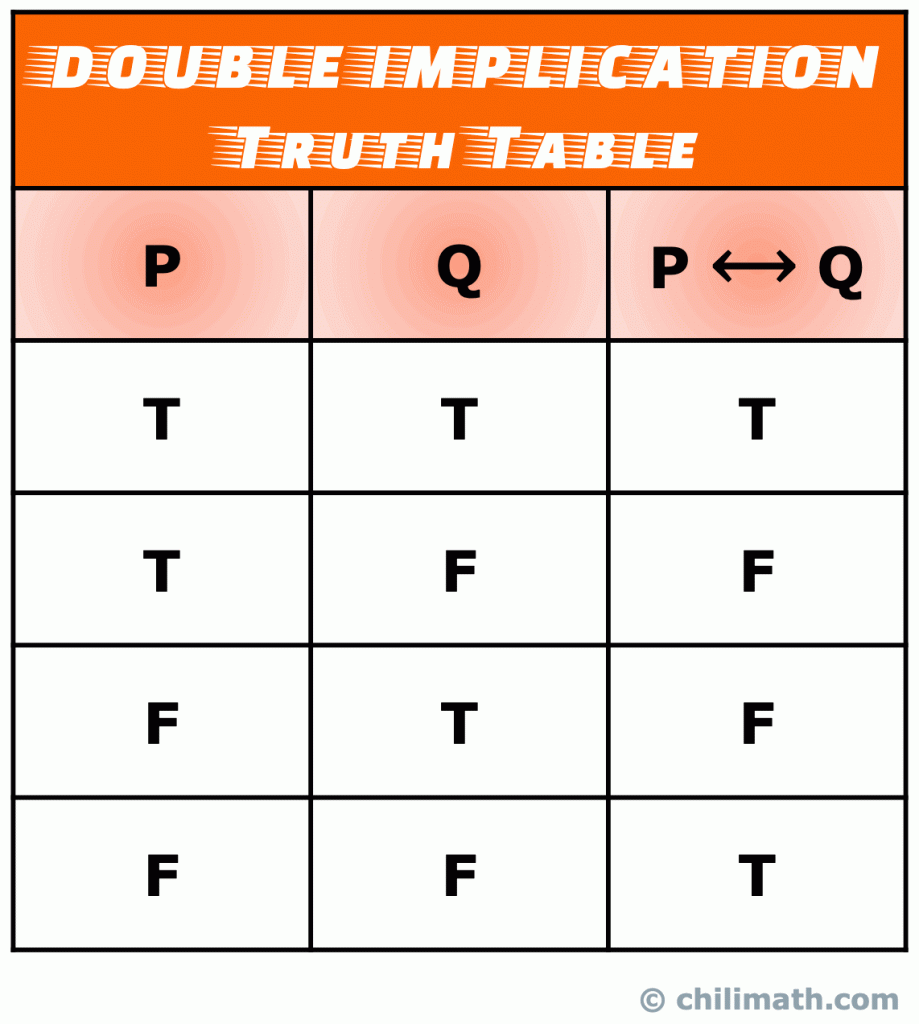
recuerde: el valor de verdad de la declaración bicondicional P \leftrightarrow Q es verdadero cuando ambas declaraciones simples P y Q son verdaderas o ambas falsas. De lo contrario, P \ leftrightarrow Q Es false.
Usted podría estar también interesado en:
Introducción a las Tablas de Verdad, las Declaraciones, y Conectivos Lógicos
Inversa, Inversa, y Contrapositivo de una sentencia Condicional
Deja una respuesta