Bayes Tilastot selitti Aloittelijoille Yksinkertainen englanti

Yleistä

• haitat frequentist tilastoja johtaa tarvetta Bayes Tilastot
• Tutustu Bayes Tilastot ja Bayes-Päättely
• On olemassa erilaisia menetelmiä testata merkitys malli, kuten p-arvo, luottamusväli, jne

Johdanto

Bayes Tilastot on edelleen käsittämätöntä vuonna syttyä mielissä monet analyytikot., Koska olemme hämmästyneitä koneoppimisen uskomattomasta voimasta, monet meistä ovat tulleet uskottomiksi tilastoille. Keskittymisemme on kaventunut koneoppimisen tutkimiseen. Eikö se ole totta?

emme ymmärrä, että koneoppiminen ei ole ainoa tapa ratkaista reaalimaailman ongelmia. Useissa tilanteissa se ei auta meitä ratkaisemaan liiketoiminnan ongelmia, vaikka näihin ongelmiin liittyy tietoa. Vähintäänkin tilastotiedon avulla voit työskennellä monimutkaisten analyyttisten ongelmien parissa tietojen koosta riippumatta.,

1770-luvulla Thomas Bayes esitteli ”Bayesin lauseen”. Vielä vuosisatoja myöhemmin ”Bayesian tilastojen” merkitys ei ole hiipunut. Itse asiassa tätä aihetta opetetaan nykyään hyvin syvissä vesissä joissakin maailman johtavissa yliopistoissa.

tämän ajatuksen, olen luonut tämän aloittelijan opas Bayes Tilastot. Olen yrittänyt selittää käsitteitä yksinkertaistavasti esimerkeillä. Ennakkotieto perustodennäköisyydestä & tilastot ovat toivottavia., Sinun pitäisi tarkistaa tämän kurssin saada kattava Alhainen tilastojen ja todennäköisyys.

loppuun Mennessä tämän artikkelin, sinun on konkreettinen käsitys Bayes Tilastot ja siihen liittyvät käsitteet.,>Bayes Lause

Bayes-Päättely

• Bernoulli todennäköisyys toiminto
• Ennen Uskomus, Jakelu
• Taka usko Jakelu

Testi Merkitys – Frequentist vs Bayes

• p-arvo
• Luottamus Väliajoin
• Bayes Factor
• High Density Interval (HDI)

Ennen kuin me itse kaivaa, Bayes Tilastot, olkaamme viettää muutaman minuutin ymmärrystä Frequentist Tilastot, enemmän suosittu versio tilastojen useimmat meistä törmännyt ja luontainen ongelmia.,

Frequentist Tilastot

keskustelu välillä frequentist ja bayes ovat ahdisti aloittelijoille vuosisatojen ajan. Siksi on tärkeää ymmärtää ero näiden kahden ja miten on olemassa ohut rajaviiva!

Se on yleisimmin käytetty johdettujen tekniikka tilastollinen maailmassa. Itseasiassa, yleensä se on ensimmäinen koulukunta, että henkilö aloittavat tilastojen maailma tulee koko.

Frequentist Tilastoja testejä, onko tapahtuma (hypoteesi) tapahtuu tai ei., Se laskee tapahtuman todennäköisyyden kokeen pitkällä aikavälillä (eli kokeilu toistetaan samoissa olosuhteissa tuloksen saamiseksi).

tässä otetaan kiinteän koon näytteenottojakaumat. Sitten kokeilu toistetaan teoriassa ääretön määrä kertoja, mutta käytännössä tehdään pysäyttävä aikomus. Esimerkiksi, minä tehdä kokeilu, jossa on tarkoitus pysäyttää mielessä, että lopetan kokeilun, kun se toistetaan 1000 kertaa tai näen vähintään 300 päät arvonnassa.

mennään nyt syvemmälle.,

nyt ymmärrämme frequentist statistiikan käyttämällä esimerkkiä kolikonheitosta. Tavoitteena on arvioida kolikon oikeudenmukaisuutta. Alla on taulukko, joka edustaa taajuus päätä:

Me tiedämme, että todennäköisyys saada pää tossing oikeudenmukainen kolikko on 0.5. No. of heads edustaa saatujen päiden todellista määrää. Difference eroa 0.5*(No. of tosses) - no. of heads.,

tärkeä asia on huomata, että vaikka ero todellinen lukumäärä ja odotettavissa lukumäärä( 50% määrä heittää) kasvaa, kun määrä heittää on lisääntynyt, osuus lukumäärä yhteensä määrä heittää lähestymistapoja 0.5 (käypä kolikko).

Tämä koe on meille hyvin yleinen virhe löytyy frequentist lähestymistapa eli Riippuvuus seurausta kokeen monta kertaa koe toistetaan.,

Jos haluat tietää lisää frequentist tilastollisista menetelmistä, voit suunnata tälle erinomaiselle kurssille inferentiaalisista tilastoista.

Frequentist statistiikan luontaiset puutteet

Till here, frequentist-tilastoissa on nähty vain yksi virhe. Se on vasta alkua.

20-luvulla näki massiivinen nousu frequentist tilastot soveltaa numeerisia malleja tarkistaa, onko yksi näyte, joka on erilainen kuin muut, parametri on tarpeeksi tärkeä pidettävä malli ja variousother ilmenemismuotoja hypoteesin testaus., Frequentist statistics kärsi kuitenkin suuria puutteita sen suunnittelussa ja tulkinnassa, mikä aiheutti vakavaa huolta kaikissa tosielämän ongelmissa. Esimerkiksi:

p-values mitataan näytteen (kiinteä koko) tilasto joitakin pysäyttää aikomus muutokset muutoksen tarkoitus ja otoksen koko. en.e, Jos kaksi henkilöä työskentelee saman tietoihin ja on eri tarkoitus pysäyttää, he voivat saada kaksi eri p- values saman tiedon, mikä ei ole toivottavaa.,

esimerkiksi: henkilö A voi päättää lopettaa kolikon heittämisen, kun kokonaismäärä on 100, kun B pysähtyy 1000: een. Eri otoskokoihin saadaan erilaisia t-pisteitä ja erilaisia p-arvoja. Samoin lopettamisaikeet voivat muuttua kiinteästä volttien määrästä kääntämisen kokonaiskestoksi. Tässäkin tapauksessa on pakko saada erilaisia p-arvoja.

2 – Confidence Interval (C. I) kuten p-value riippuu paljolti otoksen koosta., Tämä tekee pysäyttää mahdolliset täysin järjetöntä, sillä ei ole väliä kuinka monta henkilöä suorittaa testejä samat tiedot, tulosten pitäisi olla yhdenmukaisia.

3 – luottamusvälit (C. I) eivät ole todennäköisyysjakaumat näin ollen ne eivät tarjoa todennäköisin arvo, parametri, ja todennäköisin arvoja.

Nämä kolme syytä ovat tarpeeksi sinut menossa ajatella haittoja frequentist lähestymistapa ja miksi on tarvetta bayes-lähestymistapa. Otetaan selvää.,

täältä, ymmärrämme ensin Bayesilaisen tilaston perusteet.

Bayes Tilastot

”Bayes tilastot on matemaattinen menettely, joka koskee todennäköisyyksiä, tilastollisia ongelmia. Se tarjoaa ihmisille työkaluja päivittää uskomuksiaan todisteita uusista tiedoista.”

you got that? Anna minun selittää kanssa esimerkki:

Oletetaan, out of kaikki 4 mm-kilpailuihin (F1) välillä Niki Lauda ja James hunt, Niki voitti 3 kertaa kun James onnistui vain 1.,

niin, jos veikkaisit seuraavan kisan voittajaa, kuka hän olisi ?

veikkaan, että sanoisit Niki Lauda.

Here ’ s the twist. Mitä jos sinulle kerrotaan, että satoi kerran, kun James voitti ja kerran, kun Niki voitti ja on varmaa, että seuraavana päivänä sataa. Kenestä löisit rahasi vetoa ?

intuitio, se on helppo nähdä, että mahdollisuudet voittaa James on lisääntynyt rajusti. Mutta kysymys kuuluu: kuinka paljon ?,

ymmärtää ongelma käsillä, meidän täytyy olla perehtynyt joitakin käsitteitä, joista ensimmäinen on ehdollinen todennäköisyys (selitetty alla).

lisäksi, on olemassa tiettyjä ennakkoedellytyksiä:

esitietovaatimukset:

1. Linear Algebra : virkistää perusasiat, voit tarkistaa Khan Academy Algebra.
2. todennäköisyys ja perustilastot : perusasioiden virkistämiseksi voi tutustua toiseen Khan Academyn kurssiin.

3.,1 Ehdollinen Todennäköisyys

Se on määritelty: Todennäköisyys tapahtuman A koska B on yhtä suuri todennäköisyys, B ja tapahtuu yhdessä jaettuna todennäköisyys B.”

esimerkiksi: Oletetaan kaksi osittain päällekkäiset sarjat A ja B, kuten on esitetty alla.

joukko A edustaa yhtä tapahtumasarjaa ja joukko B edustaa toista. Haluamme laskea todennäköisyyden, että tietty B on jo tapahtunut. Lets edustaa tapahtumaa B varjostamalla sitä punaisella.,

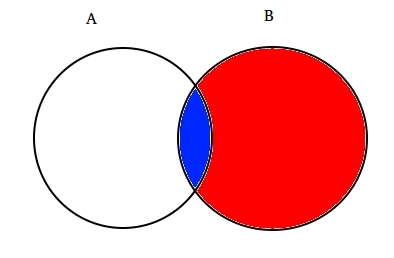
Nyt, koska B on tapahtunut, se osa, joka nyt asiat on osittain varjossa sininen, joka on mielenkiintoista . Joten, todennäköisyys tietyn B osoittautuu:

näin Ollen, voimme kirjoittaa kaava tapahtuma B koska A on jo tapahtunut:

tai

Nyt, toinen yhtälö voidaan kirjoittaa seuraavasti :

Tätä kutsutaan Ehdollinen Todennäköisyys.,

yritetään vastata vedonlyöntiongelmaan tällä tekniikalla.

oletetaan, B on James Huntin voittotapahtuma. Se on sateen tapahtuma. Siksi,

Korvaamalla arvot ehdollisen todennäköisyyden kaavaa, saamme todennäköisyys on noin 50%, mikä on lähes kaksinkertainen 25%, kun sadetta ei ole otettu huomioon (Ratkaista se teidän lopussa).

Tämä vahvisti edelleen käsitystämme James voittaa valossa uutta näyttöä en.e sadetta., Mietit varmaan, että tämä kaava muistuttaa läheisesti jotain olet ehkä kuullut paljon. Mieti!

Luultavasti, arvasit oikein. Se näyttää Bayesin Teoreemalta.

Bayesin lause on rakennettu ehdollisen todennäköisyyden päälle ja sijaitsee Bayesilaisen päättelyn sydämessä. Ymmärretään se nyt yksityiskohtaisesti.

3.2 Bayes Lause

Bayes Lause tulee voimaan, kun useita tapahtumia lomake tyhjentävä asetettu toinen tapahtuma B. Tämä voidaan ymmärtää avulla alla olevan kaavion mukaisesti.,

Nyt, B voidaan kirjoittaa

Joten, todennäköisyys B voidaan kirjoittaa,

Mutta

Niin, korvaamalla P(B) yhtälö ehdollinen todennäköisyys saamme

Tämä on yhtälö Bayes Lause.

Bayes-Päättely

ei kannata sukeltaa teoreettinen osa sitä. Opimme, miten se toimii!, Otetaan esimerkki kolikoiden heittelystä ymmärtääksemme bayesilaisen päättelyn ideaa.

tärkeä osa bayes-päättely on perustaa parametrit ja malleja.

Mallit ovat matemaattinen muotoilu havaitut tapahtumat. Parametrit ovat havaituihin tietoihin vaikuttavien mallien tekijöitä. Esimerkiksi kolikon heittelyssä kolikon oikeudenmukaisuus voidaan määritellä θ: n merkitsemän kolikon parametriksi. Tapahtumien lopputuloksen voi merkitä D.

vastaa tähän nyt., Mikä on todennäköisyys 4 päätä 9 hesses(d) ottaen huomioon oikeudenmukaisuus kolikon (θ). en.e P(D|θ)

Odota, minä kysyä oikea kysymys? Ei.

– Meidän pitäisi olla enemmän kiinnostunut tietää : Koska lopputulos (D) mikä on probbaility kolikon reilu (θ=0.5)

Avulla edustaa sitä käyttäen Bayes Lause:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

Tässä, P(θ) – on, ennen en.e vahvuus uskomme, että oikeudenmukaisuus kolikon ennen heitä., On täysin ok uskoa, että kolikolla voi olla minkäänlaista oikeudenmukaisuutta välillä 0 ja 1.

P(D|θ) todennäköistä on, että tarkkailemalla tulos koska meidän jakelu θ. Jos tietäisimme, että kolikko on reilu, tämä antaa todennäköisyyden tarkkailla päiden määrää tietyssä määrässä voltteja.

P(D) todisteet. Tämä on datan todennäköisyys, joka määritetään summaamalla (tai integroimalla) kaikki mahdolliset θ: n arvot, painotettuna sillä, kuinka vahvasti uskomme näihin θ: n arvoihin.,

Jos meillä oli useita näkemyksiä siitä, mitä oikeudenmukaisuus kolikko on (mutta en tiedä varmasti), niin tämä kertoo meille, todennäköisyys nähdä tietyssä järjestyksessä kääntää kaikki mahdollisuudet uskomme, että kolikko on oikeudenmukaisuus.

P(θ|D) on taka usko meidän parametrit todettuaan todisteita i.e määrä päitä .

täältä sukellamme syvemmälle tämän käsitteen matemaattisiin vaikutuksiin. Älä huoli. Kun niitä ymmärtää, sen matematiikkaan pääseminen on aika helppoa.,

jotta mallimme voidaan määritellä oikein , tarvitaan kaksi matemaattista mallia ennen kättä. Toinen edustaa todennäköisyysfunktiota P (D / θ )ja toinen edeltävien uskomusten jakautumista. Näiden kahden tuote antaa posteriorisen uskomuksen P (θ|d) jakauman.

Koska ennen ja posterior ovat molemmat uskomuksia jakautumisen oikeudenmukaisuus kolikon, intuitio kertoo, että molemmilla pitäisi olla sama matemaattinen muoto. Pidä tämä mielessä. Palaamme siihen vielä.,

joten on olemassa useita funktioita, jotka tukevat Bayesin lauseen olemassaoloa. Niiden tunteminen on tärkeää, joten olen selittänyt ne yksityiskohtaisesti.

4.1. Bernoullin todennäköisyysfunktio

antaa kerrata, mitä opimme todennäköisyysfunktiosta. Joten, olemme oppineet, että:

Se on todennäköisyys tarkkailla tietty määrä päät tietyn määrän voltteja tietyn oikeudenmukaisuuden kolikon. Tämä tarkoittaa, että Kruuna/klaava-todennäköisyytemme riippuu kolikon oikeudenmukaisuudesta (θ).,

P(y=1|θ)=

P(y=0|θ)=

huomion arvoista on, että eli 1 niin päätä ja 0, kun hännät on vain matemaattinen notaatio laatia malli. Voimme yhdistää edellä mainitut matemaattiset määritelmät yhdeksi määritelmä edustaa todennäköisyys sekä tuloksia.

P(y|θ)=

Tätä kutsutaan Bernoulli-uskottavuusfunktio ja tehtävä kolikon flipping kutsutaan Bernoullin kokeet.,

y={0,1},θ=(0,1)

Ja kun me haluamme nähdä sarjan päät tai voltteja, sen todennäköisyys on annettu:

Lisäksi, jos olemme kiinnostuneita todennäköisyys lukumäärä z kääntämällä ylös N määrä voltteja niin todennäköisyys on annettu:

4.2. Ennen Uskomus, Jakelu

Tämä jakelu on käytetty edustamaan meidän vahvuuksista uskomuksia parametrit perustuvat aikaisempaan kokemukseen.,

mutta, entä jos jollakulla ei ole aiempaa kokemusta?

Älä huoli. Matemaatikot ovat keksineet keinoja tämänkin ongelman lieventämiseksi. Se tunnetaan nimellä uninformative priors. Haluan ilmoittaa teille etukäteen, että se on vain harhaanjohtava. Jokainen epätietoinen priori tarjoaa aina jonkin informaatiotapahtuman jatkuvan jakautumisen ennen.

No, matemaattinen funktio käytetään edustamaan ennen uskomuksia tunnetaan beta distribution., Sillä on joitakin erittäin mukavia matemaattisia ominaisuuksia, joiden avulla voimme mallintaa uskomuksiamme binomijakaumasta.

tiheysfunktion beta-jakauma on muotoa :

jossa meidän painopiste pysyy osoittaja. Nimittäjä on olemassa vain sen varmistamiseksi, että kokonaistodennäköisyysfunktio integraation yhteydessä arvioi 1.

α ja β kutsutaan muoto päätetään parametrit tiheysfunktio., Täällä α on analoginen lukumäärä tutkimuksissa ja β vastaa määrää hännät., Kaaviot auttavat sinua visualisoida beta-jakaumia eri arvot α ja β

sinäkin Voit piirtää beta-jakelu itse, käyttäen seuraava koodi R:

Huom! α ja β ovat intuitiivisia ymmärtää, koska ne voidaan laskea tuntemalla keskiarvo (μ) ja keskihajonta (σ) jakelu., Itse asiassa, ne liittyvät niin :

Jos keskiarvo ja keskihajonta, jakelu ovat tiedossa , sitten on muoto parametrit voidaan helposti laskea.

Päättely peräisin kaaviot yllä:

1. Kun ei nakata me uskotaan, että jokainen oikeudenmukaisuus kolikko on mahdollista, kuten on kuvattu tasainen viiva.
2. Kun oli enemmän määrä päät kuin hännät, kuvaaja osoitti huippu siirtynyt kohti oikealla puolella, osoittaa suurempi todennäköisyys päät, ja että kolikko ei ole tasapuolinen.,
3. mitä enemmän heittää ovat tehneet, ja päät tulevat edelleen suurempi osa huippu kapenee lisätä meidän luottamusta oikeudenmukaisuuden kolikon arvo.

4, 3. Taka Usko Jakelu

syy siihen, että valitsimme ennen uskomus on saada beta-jakauma. Tämä johtuu siitä, kun me kerrotaan se uskottavuusfunktio, posterior-jakauma saadaan muoto samanlainen ennen-jakelu, joka on paljon helpompi samaistua ja ymmärtää., Jos tämä tieto piristää ruokahaluasi, olet varmasti valmis kävelemään yli kilometrin.

lasketaan posteriorinen uskomus Bayesin lauseella.

Laskeminen taka usko käyttäen Bayes Lause

Nyt, meidän posterior uskosta tulee,

Tämä on mielenkiintoinen., Vain tietäen, keskiarvo ja standardi jakelu uskoamme siitä, parametri θ ja tarkkailemalla lukumäärä N voltteja, voimme päivittää käsitystämme siitä, mallin parametri(θ).

Antaa ymmärtää, tämän avulla yksinkertainen esimerkki:

Oletetaan, että, luulet, että kolikko on puolueellinen. Sen keskihajonta (μ) on noin 0,6 ja keskihajonta 0,1.

.

α= 13.8 , β=9.2

en.,jakelumme on puolueellista oikealla puolella. Oletetaan, havaitaan 80 päät (z=80) 100 volttia(N=100). Katsotaan, miten meidän ennen ja taka uskomukset ovat menossa katsomaan:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

Avulla visualisoida sekä uskomukset kuvaaja:

T-koodi edellä kuvaaja on kuin:

}

enemmän ja enemmän voltteja on tehty ja uudet tiedot on havaittu, uskomuksemme saada päivitetty., Tämä on Bayesilaisen päättelyn todellinen voima.

Testi Merkitys – Frequentist vs Bayes

menemättä tiukkaa matemaattisia rakenteita, tämä osio antaa sinulle nopean yleiskatsauksen eri lähestymistapoihin frequentist ja bayes menetelmiä testata merkitys ja ero ryhmien välillä ja mikä menetelmä on luotettavin.

5.1. p-arvo

tässä, t-pisteet tietyn näyte näytteenotto jakelu kiinteä koko lasketaan. Sitten ennustetaan p-arvoja., Voimme tulkita p-arvot seuraavasti (esimerkiksi p-arvo 0,02 keskiarvon 100 jakaumassa) : on 2% todennäköisyys, että otoksen keskiarvo on 100.

Tämä tulkinta kärsii virhe, että näytteenotto jakaumat eri kokoisia, yksi on pakko saada eri t-score ja siten eri p-arvo. Se on täysin järjetöntä. P-arvo on alle 5% ei takaa, että nollahypoteesi on väärä eikä p-arvo on suurempi kuin 5% varmistaa, että nollahypoteesi on oikea.

5, 2., Luottamusvälit

luottamusvälit myös kärsiä sama vika. Lisäksi, koska C. minulla ei ole todennäköisyysjakauma , ei ole mitään keinoa tietää, mitkä arvot ovat todennäköisin.

5, 3. Bayes Factor

Bayes-tekijä on vastaava p-arvo bayes puitteissa. Lets ymmärtää sen kokonaisvaltaisesti.

nollahypoteesi vuonna bayes puitteissa oletetaan,∞: n todennäköisyysjakauma vain tietyn parametrin arvoa (eli θ=0.5) ja nolla todennäköisyys muuta missä., (M1)

vaihtoehtoinen hypoteesi on, että kaikki arvot θ ovat mahdollisia, joten tasainen käyrä, joka edustaa jakelu. (M2)

nyt uuden tiedon posteriorinen jakautuminen näyttää alla.

Bayes tilastot säätää uskottavuuden (todennäköisyyden) eri arvot θ. Se voidaan helposti nähdä, että todennäköisyysjakauma on siirtynyt kohti M2, joiden arvo on suurempi kuin M1 minä.e M2 on todennäköisempää.,

Bayes-tekijä ei ole riippuvainen todellinen jakauman arvot θ mutta suuruusluokka muutos arvot M1 ja M2.

paneelissa a (esitetty yllä): vasen palkki (M1) on nollahypoteesin ennakkotodennäköisyys.

paneelissa B (esitetty) vasen palkki on nollahypoteesin posteriorinen todennäköisyys.

Bayes-tekijä on määritelty suhde posterior kertoimet ennen kertoimet,

hylätä nollahypoteesi, BF <1/10 on edullinen.,

Voimme nähdä välittömiä etuja käyttämällä Bayes-Tekijä sen sijaan, p-arvot, koska ne ovat riippumattomia aikomuksia ja otoksen koko.

5, 4. High Density Interval (HDI)

HDI muodostuu posterior distribution jälkeen tarkkailemalla uusia tietoja. Koska HDI on todennäköisyys, 95% HDI antaa 95% uskottavimmat arvot. Se on myös taattu, että 95 % arvoista on valhe tämä väli toisin kuin C. I.

Huomaa, miten 95%: n HDI ennen jakelu on laajempi kuin 95% taka-jakelu., Tämä johtuu siitä, että uskomme HDI: hen kasvaa havaitessamme uutta tietoa.

End Huomautuksia

tämän artikkelin tavoitteena oli saada sinut ajattelemaan eri tyyppi tilastollinen filosofiat siellä ja miten jokin yksittäinen niitä ei voi käyttää joka tilanteessa.

Se on korkea aika, että molemmat filosofiat ovat sulautuneet lieventämiseksi reaalimaailman ongelmia puuttumalla puutteita muiden., Tämän sarjan II osassa keskitytään mitoituksen Vähentämistekniikoihin MCMC: n (Markov-ketju Monte Carlo) algoritmien avulla. III osa tulee perustua luoda Bayesian regression malli tyhjästä ja tulkita sen tuloksia R. Joten, ennen kuin aloitan Osa II, en haluaisi olla teidän ehdotuksia / palautetta tämän artikkelin.