Binomijakauman

”Bi” tarkoittaa ”kaksi” (kuten polkupyörä on kaksi pyörää) … … kyse on siis asioista, joilla on kaksi tulosta.,

Heitetään Kolikkoa!

heitä reilu kolikko kolmesti … mikä on mahdollisuus saada kaksi päätä?,tr>

THH THT TTH TTT

Which outcomes do we want?,

” kaksi päätä ”voisi olla missä järjestyksessä tahansa:” HHT”,” THH ”ja” HTH ” kaikilla on kaksi päätä (ja yksi häntä).

niin 3 lopputuloksesta syntyy ”kaksi päätä”.

mikä on kunkin tuloksen todennäköisyys?,operaatiot ovat (P tarkoittaa ”Todennäköisyys”):

• P(Kolme Päätä) = P(HHH) = 1/8
• P(Kaksi Päätä) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Yksi Pää) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Nolla Päät) = P(TTT) = 1/8

Voimme kirjoittaa tämän suhteen on satunnaismuuttujan X = ”määrä Päät alkaen 3 heittää kolikon”:

• P(X = 3) = 1/8
• P(X = 2) = 3/8
• P(X = 1) = 3/8
• P(X = 0) = 1/8

Ja tämä on mitä se näyttää, koska kuvaaja:

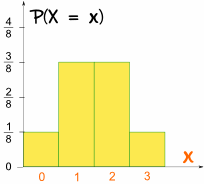
Se on symmetrinen!,

Joten Kaava

kuvittele Nyt, haluamme mahdollisuudet 5 päänsä heittää 9: luetella kaikki 512 tulokset kestää pitkään!

Joten tehdään kaava.

edellisessä esimerkissämme, miten saamme arvot 1, 3, 3 ja 1 ?

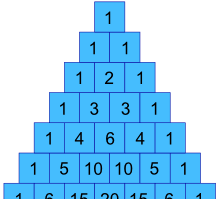
– he ovat todella Pascalin Kolmio !

Voimmeko tehdä ne kaavalla?

Varma, että voimme, ja tässä se on:

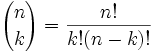
Se on usein kutsutaan ”n choose k”

• n = määrä yhteensä
• k = numero haluamme
• ”!,”tarkoittaa ” factorial”, esimerkiksi 4! = 1×2×3×4 = 24

Voit lukea lisää aiheesta Yhdistelmät ja Permutaatiot.

kokeillaan.

katsotaanpa käyttää sitä vaikeampaa kysymys:

Bias!

toistaiseksi onnistumisen tai epäonnistumisen mahdollisuudet ovat olleet yhtä todennäköiset.

mutta entä jos kolikot ovat puolueellisia (maata enemmän toisella puolella kuin toisella) tai valinnat eivät ole 50/50.

katsotaanpa piirtää puu kaavio:

”Kaksi Kanaa” tapauksissa on korostettu.

todennäköisyydet ”kaksi kanaa” kaikki työ on 0.147, koska olemme kertomalla kaksi 0.7 s ja yksi 0.3 kussakin tapauksessa. Toisin sanoen

0.147 = 0.7 × 0.7 × 0.3

Tai, käyttäen eksponenttien:

= 0.72 × 0.31

0,7 on todennäköisyys jokaiselle valinta haluamme kutsua sitä p

2 on useita vaihtoehtoja, haluamme kutsua k

Ja meillä on (toistaiseksi):

= pk × 0.31

0.,3 on todennäköisyys, vastakkaista valinta, niin se on: 1−p

1 on määrä vastakkaista vaihtoehtoa, niin se on: n−k

Joka antaa meille:

= pk(1-p)(n-k)

Missä

• p on todennäköisyys jokaiselle valinta haluamme
• k on useita vaihtoehtoja, haluamme
• n on kokonaismäärä valintoja

Nyt tiedämme, että todennäköisyys jokaiselle tulokselle on 0.147

OK. Se oli paljon työtä jotain tiesimme jo, mutta nyt meillä on kaava, voimme käyttää kovempaa kysymyksiä.,

koonnut

Nyt me tiedämme, miten laskea, kuinka monta:

n!k!(n-k)!

Ja todennäköisyys kunkin:

pk(1-p)(n-k)

Kun kerrotaan yhdessä saamme:

Tärkeää:

• kokeet ovat riippumattomia,
• On olemassa vain kaksi mahdollista lopputulosta jokaisessa tutkimuksessa,
• todennäköisyys sille, ”menestys” on jokainen oikeudenkäynti on vakio.,

Quincunx

On pelata Quincunx (lue Quincunx Selitti) nähdä binomijakauman toiminnassa.

Heittää arpa

reilun kuolla heitetään neljä kertaa. Laske todennäköisyydet saada:

• 0 Kakkosta
• 1 Kaksi
• 2 Kakkosta
• 3 Kakkosta
• 4 Kakkosta

tässä tapauksessa n=4, p = P(Kaksi) = 1/6

X on Satunnainen Muuttuja Numero Kaksittain neljä heittää’.,

korvaa X = 0-4 kaavaksi:

P(k pois n) = n!k!(n-k)! pk(1-p)(n-k)

Kuten tämä (4 desimaalin tarkkuudella):

Tällä kertaa kuvio ei ole symmetrinen:

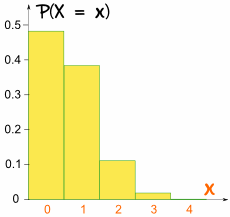
Se ei ole symmetrinen!

Se on vinossa, koska p ei ole 0.5

Urheilu Polkupyörää

Yrityksesi tekee urheilu polkupyörää. 90% läpäisee lopputarkastuksen (ja 10% epäonnistuu ja on vahvistettava).

mikä on 4 seuraavan tarkastuksen odotettu keskiarvo ja varianssi?

ensin lasketaan kaikki todennäköisyydet.,

• n = 4,
• p = P(Pass) = 0.9

X on Satunnainen Muuttuja ”Määrä kulkee neljä tarkastukset”.

korvaa X = 0-4 kaavaksi:

P(k pois n) = n!k!(n-k)! pk(1-p)(n-k)

Keskiarvo, Varianssi ja Keskihajonta

laske Keskiarvo, Varianssi ja Keskihajonta Urheilu Pyörä tarkastuksia.

niille on (suhteellisen) yksinkertaiset kaavat. Niitä on vähän vaikea todistaa, mutta ne tekevät työtä!,

tarkoitan, tai ”odotusarvo” on:

μ = np

kaava Varianssi on:

Varianssi: σ2 = np(1-p)

Ja Keskihajonta on neliöjuuri varianssi:

σ = sqrt(np(1-p))