Budjettikohta: Huomautuksia budjettikohta, Tilaa, Muutoksia ja Kaltevuus

tiedon käsitteen budjettikohdan tai mitä kutsutaan myös budjettirajoite on ymmärtämisen teoria kuluttajan tasapaino.

suurempi välinpitämättömyyskäyrä osoittaa suurempaa tyytyväisyyttä kuin alempi. Siksi kuluttaja, joka yrittää maksimoida tyytyväisyytensä, yrittää päästä korkeimpaan mahdolliseen välinpitämättömyyskäyrään.,

Mutta hänen harjoittamisesta ostaa enemmän ja enemmän tavaroita ja näin saada enemmän ja enemmän tyydytystä hänellä on työn alla kaksi ehtoa: ensinnäkin, hän on maksaa hinnat tavaroiden ja toiseksi, hän on rajoitetusti rahaa tulot, joilla voit ostaa tavaroita. Näin, kuinka pitkälle hän menisi hänen ostot riippuu hinnat tavaroiden ja rahaa tulot, jotka hän on viettää tavaroista.,

jotta voitaisiin selittää kuluttajan tasapaino on myös tarvetta ottaa käyttöön osaksi välinpitämättömyys käyrä analyysi budjettikohta, joka edustaa hinnat tavaroiden ja kuluttaja on rahaa tuloja.

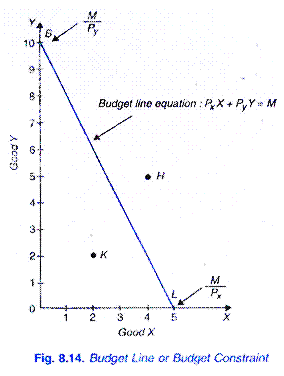
Oletetaan, että kuluttaja on saanut tuloja Rs. 50 viettää kaksi tavaraa X ja Y. anna hinta hyvä X markkinoilla RS. 10 per yksikkö ja Y Rs. 5 yksikköä kohti. Jos kuluttaja käyttää koko tulonsa Rs. 50 hyvä X, hän ostaisi 5 yksikköä X; jos hän käyttää koko tulonsa Rs., 50 hyvä Y hän ostaisi 10 yksikköä Y. Jos suora viiva 5Xand 10Vis vetoa, saamme mitä kutsutaan hinta-rivi tai budjettikohta.

Näin ollen talousarvion rivillä näkyy kaikkien näiden yhdistelmiä kaksi tavaroita, jotka kuluttaja voi ostaa viettämällä hänen antanut rahaa tuloja kaksi tavarat niiden hinnat. Katso Figiä. 8.14 osoittaa, että Rs. 50, ja hinnat X ja Y on Rs-10 Rs. 5 vastaavasti kuluttaja voi ostaa l0Y ja OX, tai Seistä IX; tai 6Y-ja 2X, tai 4y ja 3X jne.,

Toisin sanoen, hän voi ostaa tahansa seos, joka sijaitsee talousarvion mukaisesti hänen antanut rahaa tuloja ja koska tavaroiden hinnat. On huomattava, että kaikki näiden kahden tavaran, kuten H: n (5Y ja 4x), yhdistelmät, jotka sijaitsevat kyseisen budjettikohdan yläpuolella ja ulkopuolella, ovat kuluttajan ulottumattomissa.

Mutta mitä tahansa makaa sisällä budjettikohdan kuten K (2X ja 2Y) on hyvin sisällä reach-kuluttaja, mutta jos hän ostaa tällaisen yhdistelmän, hän ei viettää kaikki hänen tuloja Rs. 50., Näin ollen, olettaen, että koko koska tulot on käytetty tietyn tavaroiden ja koska hinnat niistä, kuluttajan on valita kaikki ne yhdistelmät, jotka makaavat budjettikohta.

edellä mainitusta budjettikohdasta käy selvästi ilmi, että budjettirajoitus on rajattu. Yhdistelmät hyödykkeiden makaa oikealla budjettikohdan ovat saavuttamattomissa, koska tulot kuluttaja ei riitä ostaa näiden yhdistelmiä., Koska kuluttajan tulot ja hinnat kahden tavaroiden yhdistelmiä tavarat makaa vasemmalla budjettikohtaan on mahdollista, että kuluttaja voi ostaa minkä tahansa yksi heistä.

on myös tärkeää muistaa, että Y-akselin ob pysäytetään Kuvassa. 8,14 tarkoittaa hänen koko tulonsa määrää (M) jaettuna hyödyke Y: n hinnalla (PY) eli OB = M/PY. Samoin X-akselin intercept OL mittaa kokonaistuloja jaettuna hyödykkeen X hinnalla. näin ollen OL = M/Px.,

budjettikohtaan voidaan kirjoittaa algebrallisesti seuraavasti:

Missä Px ja Py merkitsevät hintojen tavaroiden X ja Y vastaavasti ja M tarkoittaa rahaa tuloja:

edellä budjetti-line yhtälö (1) merkitsee sitä, että annetaan rahaa, tulot kuluttajien ja hinnat kahden tavaroiden, jokainen yhdistelmä makaa budjettikohdan maksaa saman määrän rahaa, ja voi siksi olla ostettu annetaan tulot., Budjettikohtaan voidaan määritellä joukko yhdistelmiä kaksi hyödykkeitä, joita voi ostaa, jos koko koska tulot on käytetty niitä ja sen kulmakerroin on yhtä suuri negatiivinen hinta-suhde.

Talousarvio Tilaa:

Sen pitäisi olla huolellisesti ymmärtää, että budjetti yhtälö PxX + PyY= M Y = M/Py – Px/PyX kuvattu budjettikohdan Kuviossa. 8.14 kuvataan ainoastaan budjettikohta eikä budjettikohta., Budjetti tilaa näyttää joukko kaikki yhdistelmät kaksi hyödykkeitä, joita voi ostaa viettämällä koko-tai osa annetaan tulot.

Toisin sanoen, budjetti tilaa edustaa mahdollisuus asettaa kuluttajalle, että on, kaikki ne yhdistelmät kaksi hyödykkeitä, jotka hän voi ostaa, koska hänen budjettirajoite. Näin ollen talousarvio tilaa merkitsee asetettu kaikkien yhdistelmiä kaksi tavaroita, joiden tuotot käytetään hyvä X (eli PxX ja tuotot käytetään hyvä Y (eli PyY) ei saa ylittää antanut rahaa tuloja.,

näin Ollen, voimme algebrallisesti ilmaista talousarvion tilaa seuraavassa muodossa epätasa-arvoa:

PxX + PyY < M, tai M > PxX + PyY

talousarvion tilaa on graafisesti esitetty Kuviossa. 8.15 varjostettuna alueena. Budjettikohta on koko budjettikohdan BL ja kahden toimintalinjan rajaama alue.

hinnanmuutokset ja budjettikohdan muutos:

nyt, mitä budjettikohdalle tapahtuu, jos joko tavaroiden hinnat muuttuvat tai tulot muuttuvat., Tarkastelkaamme ensin tavaroiden hintojen muutoksia. Tämä käy ilmi viikunasta. 8.16. Oletetaan budjettikohdan alussa on BL, kun otetaan huomioon tietyt hinnat tavaroiden X ja Y ja tietty tulo. Oletetaan hinta X laskee, Hinta Y ja tulot pysyvät ennallaan. Nyt, jolla on pienempi hinta X kuluttaja voi ostaa lisää määrä X ennen kuin hänen annetaan tulot.

Anna at alempi hinta X, koska tuotot ostot OL’ X, joka on suurempi kuin VANHA., Koska hinta Y pysyy samana, ei voi olla mitään muutosta ostettu määrä hyviä Y samalla annetaan tulot ja tämän seurauksena siellä tulee olla muutos pisteeseen B. Näin ollen, lasku hinta hyvä X, kuluttajan rahat, tulot ja hinta Y pysyi muuttumattomana, talousarvion viiva siirtyy oikealle ja uusi asema BL’.,

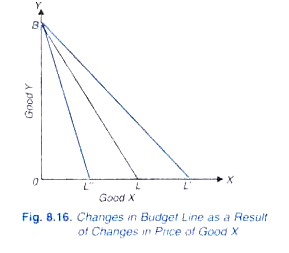
Nyt, mitä tapahtuu budjettikohta (alkuperäinen talousarvio line BL) jos hinta hyvä X nousee, hinta hyvä Y ja tuloja jäljellä muuttamattomina. Kun hinta on hyvä X, kuluttaja voi ostaa pienemmän määrän X, sano OL ” kuin ennen. Niinpä X: n hinnannousun myötä budjettikohta siirtyy vasemmalle uudelle positiolle BL”.

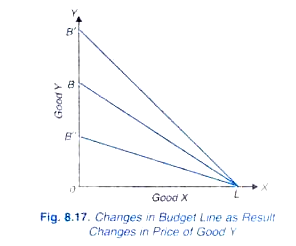
kuva 8.,17 näyttää budjettikohdan muutokset, kun hyvän Y: n hinta laskee tai nousee, jolloin X: n hinta ja tulot pysyvät samoina. Tässä alkuperäinen budjettikohta on BL. Kanssa lasku hinta hyvä Y, muiden tekijöiden pysyessä ennallaan, kuluttaja voisi ostaa enemmän Y: n kanssa, koska rahan tulo ja sen vuoksi budjettikohdan siirtyy edellä LB’. Samoin, kun hinnannousu Y, muut asiat ovat vakio, budjettikohta siirtyy alle LB”.,

Muutokset Tulojen ja muutokset Talousarvio line:

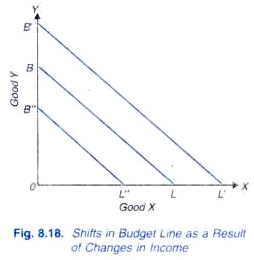
Nyt, kysymys on, mitä tapahtuu talousarvion rivillä, jos tulot muuttuvat, kun tuotteiden hinnat pysyvät samoina. Tulomuutosten vaikutus budjettikohtaan näkyy kuvassa. 8.18. Olkoon BL alkuperäinen budjettikohta, kun otetaan huomioon tietyt tavaroiden ja tulojen hinnat. Jos kuluttajan tulot kasvaa, kun hinnat sekä tuotteiden X ja y pysyvät ennallaan, hinta linja siirtyy ylöspäin (sanoa, BL’) ja on yhdensuuntainen alkuperäisen talousarvion line BL.,

Tämä on, koska lisääntynyt tulot kuluttaja voi ostaa suhteellisesti suurempi määrä hyvä X kuin ennen, jos koko tulo on käytetty X, ja vastaavasti suurempi määrä hyvä Y kuin ennen, jos koko tulo on käytetty Y. toisaalta, jos tulot kuluttajien vähenee, hinnat sekä tuotteiden X ja Y pysyvät ennallaan, budjettikohdan siirtyy alaspäin (eli B”L”) mutta edelleen rinnakkain alkuperäinen hinta line BL.,

Tämä on, koska alemman tulotason ostaa suhteellisesti pienempi määrä hyvä X, jos koko tulo on käytetty X ja suhteellisesti pienempi määrä hyvä Y, jos koko tulo on käytetty Y.

on selvää, ylhäältä, että budjettikohta on muutos, jos joko tuotteiden hinnat muuttuvat tai tulot kuluttajien muutoksia.

Näin ollen, nämä kaksi tekijät budjettikohdan ovat:

(a) hinnat tavaroiden ja

(b) kuluttajan tulot on käytetty tavara.,

Rinne budjettikohdan ja Hinnat Kaksi Tavarat:

Se on myös tärkeää muistaa, että kaltevuus budjettikohta on yhtä suuri kuin suhde hinnat kaksi tavaroita. Tämä voidaan todistaa Figin avulla. 8.14. Oletetaan ottaen huomioon tuloja kuluttaja on M ja koska hinnat hyödykkeiden X ja Y ovat Px ja Py vastaavasti.

budjettikohdan Bl kaltevuus on OB / OL. Aiomme todistaa, että tämä Rinne on yhtä suuri kuin suhde hinnat tavaroiden X ja Y.,

määrä hyvä X ostaa jos koko koska tulot M on viettänyt sitä on OL. Siksi OL x Px = M

OL = M/Px

Nyt, määrä hyvä Y ostaa jos koko koska tulot M on viettänyt sitä on OB.

Se on näin osoittanut, että rinne budjettikohdan BL on yhtä suuri kuin suhde hinnat kahden tavaroita.