CALC RESOURCE (Suomi)

Teoreettinen tausta

sisällysluettelo

Johdanto

ulokepalkin on yksi kaikkein yksinkertaisia rakenteita. Siinä on vain yksi tuki, yksi sen päistä. Tuki on niin sanottu kiinteä tuki että estää kaikki liikkeet, mukaan lukien pysty-tai vaaka-siirtymät sekä kaikki kierrosta. Toinen pää on tukematon, ja siksi se on vapaasti liikkua tai kiertää. Tätä vapaata päätä kutsutaan usein cantileverin kärjeksi.,

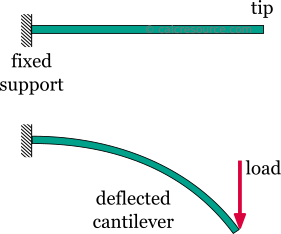
Poistaminen kärventää tukea tai lisäämällä sisäisen sarana, tekisi ulokepalkin osaksi mekanismi: kehon liikkeet ilman rajoituksia yhdessä tai useammassa suuntiin. Tämä on ei-toivottu tilanne kuorman kantorakenteelle. Tämän seurauksena cantilever palkki ei tarjoa irtisanomisia tukia. Jos paikallinen vika tapahtuisi, koko rakenne romahtaisi., Tällaisia rakenteita, jotka eivät tarjoa irtisanomista, kutsutaan kriittisiksi tai määrääviksi rakenteiksi. Sitä vastoin rakennetta, jossa on enemmän tukia kuin sen vapaan liikkumisen rajoittamiseksi vaaditaan, kutsutaan tarpeettomaksi tai epämääräiseksi rakenteeksi. Cantilever-palkki on determinantti rakenne.

Oletukset

staattinen analyysi tahansa kuorma kuljettaa rakenne liittyy arvio sen sisäiset voimat ja momentit, sekä sen taipumat., Tyypillisesti, koneen rakenne, jossa lento -, lastaus -, sisäisten toimien kohteita ovat aksiaalinen voima N , poikittainen leikkausvoima V ja taivutusmomentti M . Vain poikittaisia kuormia kuljettavan kantolavan aksiaalivoima on aina nolla, kunhan taipumat ovat pieniä. Siksi on melko tavallista laiminlyödä aksiaaliset voimat.,

lasketut tulokset tällä sivulla perustuvat seuraaviin oletuksiin:

• materiaali on homogeeninen ja isotrooppinen (toisin sanoen sen ominaisuudet ovat samat osoitat ja kohti tahansa suuntaan)
• materiaali on lineaarinen joustava
• kuormituksia staattinen tavalla (ne eivät muutu ajan)
• poikkileikkaus on sama koko palkin pituus
• taipumat ovat pieniä
• Jokainen poikkileikkaus, joka alun perin on kone ja myös normaalia pituusakseliin nähden, pysyy koneessa ja normaali taipuneen akselin liian., Tämä on silloin, kun poikkileikkauksen korkeus on melko pienempi kuin säteen pituus (10 kertaa tai enemmän) ja myös poikkileikkaus ei ole monikerroksinen (ei voileipä tyyppi-kohdassa).

kaksi viimeistä oletukset täyttävät kinemaattinen vaatimukset Euler-Bernoulli palkki teoria, joka on hyväksytty myös täällä.

Sign convention

sisäisten voimien ja momenttien laskemiseksi missä tahansa palkin leikkauskohdassa tarvitaan merkkisopimus., Seuraavat ovat hyväksytty täällä:

1. aksiaalinen voima on positiivinen, kun se aiheuttaa jännitteitä osa
2. leikkaus voima on positiivinen, kun se aiheuttaa myötäpäivään kierto osa.
3. taivutusmomentti on positiivinen, kun se aiheuttaa jännitteitä alemman kuitua palkin ja puristus päälle kuitua.

nämä säännöt, joskaan eivät pakollisia, ovat melko yleismaailmallisia. Erilaiset säännöt, jos niitä noudatettaisiin johdonmukaisesti, tuottaisivat myös samat fyysiset tulokset.,e, V, ja taivutusmomentti M

Symbolit

• E : materiaalin kimmokerroin (Young ’ s modulus)
• I : hitausmomentti poikkileikkauksen ympärille elastinen neutraali akselin taivutus
• L : koko palkin pituus
• R : tukea reaktio
• d : taipuma
• M : taivutusmomentti
• V : poikittainen leikkausvoima
• \theta : kaltevuus

ulokepalkin kanssa yhtenäinen distributed kuorma load

load-w on jaettu koko konsoli span, ottaa jatkuvasti suuruus ja suunta., Sen mitat ovat voimaa per pituus. Kokonaismäärä voima ulokepalkin on W=w L , missä L on palkin pituus. Joko kokonaisvoima W tai hajautettu voima per pituus w voidaan antaa olosuhteista riippuen.

seuraava taulukko sisältää kaavoja, joissa kuvataan staattista vastaus ulokepalkin yhtenäistä jakautunut kuorma w .

ulokepalkin kanssa piste voima kärjessä

voima on keskittynyt yhden pisteen, joka sijaitsee vapaa pää palkki., Käytännössä voima voi kuitenkin levitä pienelle alueelle, joskin alueen mittojen tulisi olla huomattavasti kanttileveyspituutta pienemmät. Läheisyydessä voima sovellus, stressi pitoisuudet ovat odotettavissa ja tuloksena vastaus ennusti classical beam theory on ehkä epätarkkoja. Tämä on kuitenkin vain paikallinen ilmiö. Kun siirrymme pois voimapaikasta, tulokset tulevat voimaan Saint-Venantin periaatteen mukaisesti.,

seuraava taulukko sisältää kaavoja, joissa kuvataan staattista vastaus ulokepalkin alla on keskittynyt piste voima P , käyttöön kärjessä.

ulokepalkin kanssa piste voima satunnainen kanta

voima on keskittynyt yhden pisteen, missä tahansa eri puolilla ulokkeen pituus. Käytännössä voima voi kuitenkin levitä pienelle alueelle. Jotta voima voitaisiin kuitenkin pitää tiivistettynä, levitysalueen mittojen tulisi olla huomattavasti pienempiä kuin palkin pituus., Läheisyydessä voima, stressiä pitoisuudet ovat odotettavissa ja tuloksena vastaus ennusti classical beam theory ehkä epätarkkoja. Tämä on vain paikallinen ilmiö, kuitenkin, ja kun siirrymme pois voima sijainti, poikkeavat tulokset on häviävän pieni.

seuraava taulukko sisältää kaavoja, joissa kuvataan staattista vastaus ulokepalkin alla on keskittynyt piste voima P , käyttöön satunnainen etäisyys kiinteästä tukea.,

ulokepalkin kanssa kohta hetkellä

tässä tapauksessa, hetki on määrätty yhden pisteen palkki, missä tahansa eri puolilla span. Käytännössä se voisi olla voima, pari, tai jäsen vääntö, kytketty pois tasossa ja kohtisuorassa palkin.

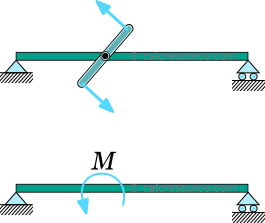
missään tapauksessa, hetki käyttöalue pitäisi levitä pieni pituus ulokkeen, niin että se voi olla onnistuneesti idealisoitu niin keskittynyt hetkellä pisteeseen., Vaikka majoitusliike, jonka lähistöltä löytyy sovellusalue, ennustaa tuloksia läpi classical beam theory odotetaan olevan epätarkkoja (johtuen stressi pitoisuudet ja muita paikallisia vaikutuksia), ennustettu tulokset ovat täysin voimassa, kun siirrymme pois, kuten Saint-Venant periaate.

seuraava taulukko sisältää kaavoja, joissa kuvataan staattista vastaus ulokepalkin alla on keskittynyt kohta hetkellä M , käyttöön etäältä kiinteästä tukea.,

ulokepalkin vaihtelevalla distributed kuorma load

kuorma jakautuu koko ulokkeen pituus, ottaa lineaarisesti eri suuruusluokkaa, alkaen w_1 kiinteällä tukea, w_2 at vapaa pää. Mitat w_1 ja w_2 ovat voimaa per pituus. Kokonaismäärä voima palkki on W={L\over2}(w_1+w_2) , missä L on ulokkeen pituus.

seuraava taulukko sisältää kaavoja, joissa kuvataan staattista vastaus ulokepalkin alle vaihtelevia jakautunut kuorma, ja puolisuunnikkaan muotoinen.,

ulokepalkin kanssa laatta-tyypin puolisuunnikkaan kuorman jakautuminen

Tämän kuorman jakautuminen on tyypillinen ulokepalkista tukemalla laatta. Jakelu näyttää oikea puolisuunnikkaan, kanssa kasvava osa lähellä kiinteä tuki ja jatkuva osa, jonka suuruus on yhtä suuri w jäljellä oleva pituus ylös kärkeen. Mitat w ovat voimaa per pituus. Kokonaismäärä voima palkki on W=w (L-a/2) , missä L on ulokkeen pituus ja a on pituus lähellä kiinteä tuki, jossa kuorman jakautuminen on vaihteleva (kolmion).,

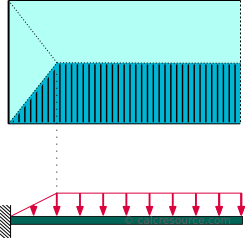
seuraava taulukko sisältää kaavoja, joissa kuvataan staattista vastaus ulokepalkin alle puolisuunnikkaan kuormituksen jakautuminen, koska laatta, kuten kuvattu kaavio edellä.

ulokepalkin kanssa osittain jaettu tasainen kuorma

kuorma on jaettu osa ulokkeen pituus, vakio suuruus w , kun taas jäljellä oleva pituus on purettu. Mitat w ovat voimaa per pituus., Kokonaismäärä voima palkki on W=w\left(L-a-b\right) , jossa L on ulokkeen pituus ja a , b puretaan pituudet vasemmalla ja oikealla puolella palkin, vastaavasti.

seuraava taulukko sisältää kaavoja, joissa kuvataan staattista vastaus ulokepalkin alle osittain jaettu tasainen kuorma.

ulokepalkin kanssa osittain jakaa puolisuunnikkaan lisää

kuorma on jaettu osa ulokkeen pituus, ottaa lineaarisesti eri suuruusluokkaa alkaen w_1, jotta w_2 , kun taas jäljellä oleva pituus on purettu., Mitat w_1 ja w_2 ovat voimaa per pituus. Kokonaismäärä voima palkki on W={L-a-b\over2}(w_1+w_2) , missä L on palkin pituus ja a , b puretaan pituudet vasemmalla ja oikealla puolella palkin vastaavasti.

Tämä on yleisin tapaus., Kaavat osittain jaettu yhtenäinen ja kolmion kuormia voi olla johdettu asianmukaisesti asetus arvot w_1 ja w_2 . Lisäksi täysin kuormatun Spanin vastaavat tapaukset voidaan johtaa asettamalla a ja b nollaan.

seuraava taulukko sisältää kaavoja, joissa kuvataan staattista vastaus ulokepalkin alle osittain jakaa puolisuunnikkaan ladata.,