|
Kaksi kolmiota ovat yhtenevät, jos ne ovat:
mutta meidän ei tarvitse tietää kaikkia kolmea puolta ja kaikkia kolmea kulmaa …yleensä kolme kuudesta riittää. |
On olemassa viisi tapaa löytää, jos kaksi kolmiota ovat yhtenevät: SSS, SAS, ASA, AAS ja HL.,
SSS (side, puolella, puolelle)
SSS tarkoittaa ”puoli, puolella, puolelle” ja tarkoittaa, että meillä on kaksi kolmiota, jossa kaikki kolme puolta yhtä.
esimerkiksi:
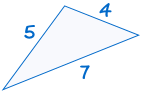 |
on congruent: | 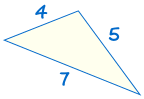 |
(Katso Ratkaisemaan SSS Kolmiot tietää enemmän)
Jos kolme puolta, kolmio on yhtä suuri kuin kolme sivua toinen kolmio, kolmiot ovat yhtenevät.,
SAS (puolella, kulmassa, puoli)
SAS on lyhenne sanoista ”puolella, kulmassa, puoli”, ja se tarkoittaa, että meillä on kaksi kolmiota, jossa tiedämme kaksi puolta ja mukana kulma ovat yhtä suuret.,
esimerkiksi:
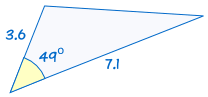 |
on congruent: | 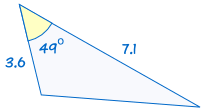 |
(Katso Ratkaisemaan SAS Kolmiot tietää enemmän)
Jos kaksi puolta ja mukana kulma yksi kolmio on yhtä suuri kuin vastaava puolta ja kulma toisessa kolmiossa, kolmiot ovat yhtenevät.,
ASA (kulma -, sivu -, kulma)
ASA sanoista ”kulma puolella kulma” ja tarkoittaa, että meillä on kaksi kolmiota, jossa tiedämme, että kaksi kulmat ja mukana puoli ovat yhtä suuret.,
esimerkiksi:
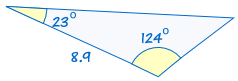 |
on congruent: | 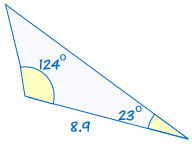 |
(Katso Ratkaisemaan ASA Kolmiot tietää enemmän)
Jos kaksi kulmat ja mukana puolella yksi kolmio on yhtä suuri kuin vastaavat kulmat ja puoli toinen kolmio, kolmiot ovat yhtenevät.,
AAS (kulma, kulma -, sivu -)
AAS sanoista ”kulman, kulmassa, puoli”, ja se tarkoittaa, että meillä on kaksi kolmiota, jossa tiedämme, että kaksi kulmat ja ei-mukana puoli ovat yhtä suuret.,
esimerkiksi:
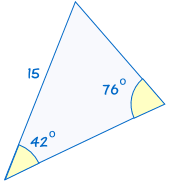 |
on congruent: | 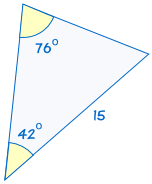 |
(Katso Ratkaisemaan AAS Kolmiot tietää enemmän)
Jos kaksi kulmat ja ei-mukana puolella yksi kolmio on yhtä suuri kuin vastaavat kulmat ja puoli toinen kolmio, kolmiot ovat yhtenevät.
HL (hypotenuusa, jalka)
Tämä koskee vain oikea kulma-kolmiot!,
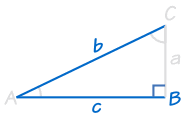 |
– tai | 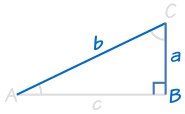 |
HL tarkoittaa ”Hypotenuusa, Jalka” (pisin puolella suorakulmaisen kolmion on nimeltään ”hypotenuusa”, kaksi muuta sivua ovat nimeltään ”jalat”)
Se tarkoittaa, että meillä on kaksi oikeus-kulma kolmiot kanssa
- sama pituus hypotenuusa ja
- sama pituus yksi muut kaksi jalkaa.
Sillä ei ole väliä mikä jalka koska kolmiot voidaan kääntää.,
esimerkiksi:
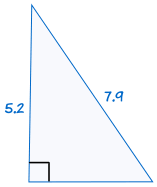 |
on congruent: | 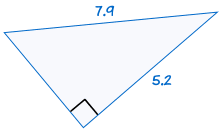 |
(Katso Pythagoraan Lause löytää lisää)
Jos hypotenuusa ja toinen jalka yhden suorakulmaisen kolmion on yhtä suuri kuin vastaava hypotenuusa ja jalka toisen suorakulmaisen kolmion, kaksi kolmiota ovat yhtenevät.
Varoitus! Älä käytä ” AAA ”
AAA tarkoittaa, että meille annetaan kaikki kolme kolmion kulmaa, mutta ei sivua.,
Tämä ei ole tarpeeksi tietoa päättää, jos kaksi kolmiota ovat yhtenevät!
Koska kolmiot voi olla sama näkökulmista, mutta eri koossa:
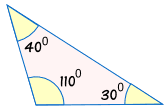 |
ei ole yhdenmukainen: | 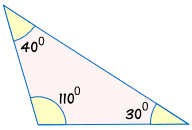 |
tietämättä vähintään toisella puolella, emme voi olla varmoja, jos kaksi kolmiota ovat yhtenevät.





Vastaa