Yksi parhaista tunnettuja matemaattisia kaavoja, on Pythagoraan Lause, joka antaa meille välinen suhde puolin suorakulmaisen kolmion. Oikea kolmio koostuu kahdesta jalasta ja hypotenuusasta. Kaksi jalat tavata 90° kulmassa ja hypotenuusa on pisin puolella suorakulmaisen kolmion ja on vastakkaisella puolella kulmassa.,
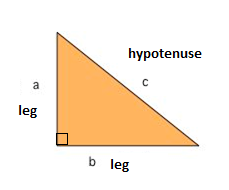
Pythagoraan Lause kertoo meille, että suhde täysi oikeus kolmio on:
$$a^{2}+b^{2}=c^{2}$$
Esimerkki
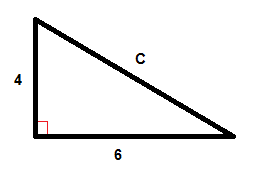
$$C^{2}=6^{2}+4^{2}$$
$$C^{2}=36+16$$
$$C^{2}=52$$
$$C=\sqrt{52}$$
$$C\n 7.2$$
On olemassa muutamia erityisiä tyyppisiä oikeus kolmiot, kuten 45°-45° oikeassa kolmioita ja 30°-60° suorakulmainen kolmio.,
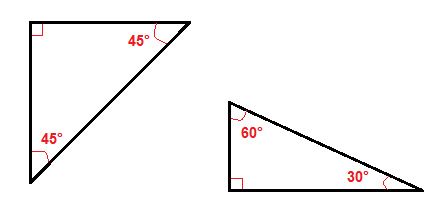
Koska niiden kulmat on helpompi löytää hypotenuusa tai jalat nämä kolmiot kuin kaikki muut oikeassa kolmioita.
45°-45° suorakulmainen kolmio, me vain täytyy kertoa yksi jalka √2 saada hypotenuusan pituus.
Esimerkki
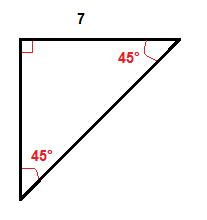
Me kerrotaan pituus jalka, joka on 7 tuumaa √2 saada hypotenuusan pituus.
$$7\cdot \sqrt{2}\n 9.,9$$
30°-60° suorakulmainen kolmio voimme löytää pituus jalan, joka on vastapäätä 30° kulmassa käyttämällä tätä kaavaa:
$$a=\frac{1}{2}\cdot c$$
Esimerkki
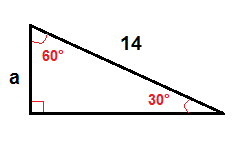
löytää, käytämme edellä esitettyä kaavaa.
$$a=\frac{1}{2}\cdot 14$$
$$a=7$$
Video oppitunti
Etsi puolin tämä kolmio
Vastaa