tällä oppitunnilla, me aiomme rakentaa viisi (5) yhteinen looginen connectives tai toimijoille. Niitä pidetään tavallisina loogisina yhteyksinä, koska ne ovat hyvin suosittuja, hyödyllisiä ja niitä opetetaan aina yhdessä.
Ennen kuin aloitamme, ehdotan, että voit tarkistaa minun muut opetus, jonka linkki on alla.
Tämä johdanto oppitunnin totuuden taulukot sisältää edellytys tieto tai tietoja, jotka auttavat sinua paremmin ymmärtää sisältöä tämän oppitunnin.,
Johdatus Totuus Taulukoita, Lausuntoja ja Connectives
Le on aloittaa luettelemalla viisi (5) yhteinen looginen connectives.
Viisi (5) Yhteinen Looginen Connectives tai Toimijoita
- Looginen Negaatio
- Looginen Konjunktio (JA)
- Looginen Ristiriita (Inklusiivinen TAI)
- Looginen Seuraus (Ehdollinen)
- Looginen Biconditional (Double Seuraus)
I., Totuustaulukko loogisesta Negaatiosta
lausuman negaatio on myös toteamus, jonka totuusarvo on täsmälleen päinvastainen kuin alkuperäisen lausuman. Esimerkiksi negaatio lausunto on kirjoitettu symbolisesti kuin
~\large{P} tai \large{\neg P}.
~{P} tai {\neg P} on lukea kuin ”S”,
Muista: negaatio-operaattori merkitään symbolilla ~ tai \neg vie totuuden arvo alkuperäinen lausuma sitten lähtö vastakohta sen totuuden arvo., Toisin sanoen negaatio yksinkertaisesti kääntää tietyn lausunnon totuusarvon. Jos siis lausunto P on totta, niin sen kieltämisen totuusarvo on väärä. Samalla tavalla, jos P on väärä, sen kieltämisen totuusarvo on totta.

II. Totuus Taulukko Looginen Konjunktio
yhdessä on eräänlainen yhdiste lausunto, joka koostuu kaksi ehdotusta (tunnetaan myös nimellä yksinkertaisia lausumia) liittyi JA operaattori.,
symbolina, jota käytetään kuvaamaan ja tai loogisena konjunktiooperaattorina, on \color{red}\Large{\wedge}. Se näyttää ylösalaisin kirjain V.
Jos meillä on kaksi yksinkertaisia lausuntoja, P ja Q, ja haluamme muodossa yhdiste lausunto liittyi JA operaattori, voimme kirjoittaa seuraavasti:
\large{P \kiila Q}.
{S \kiila Q} luetaan ”P ja Q”
Muista: totuus, arvo yhdistelmälause P \kiila Q on totta vain, jos totuus arvoja P ja Q ovat molemmat tosia., Muuten P \wedge Q on väärä.
huomaa alla olevassa totuustaulukossa, että kun P on totta ja Q on totta, P \wedge Q on totta. Kolme muuta propositioyhdistelmää P ja Q ovat kuitenkin vääriä.

III. Totuus Taulukko Looginen Ristiriita
ristiriita on eräänlainen yhdiste lausunto, joka koostuu kahdesta yksinkertaisia lausuntoja muodostettu yhdistämällä lausunnot TAI-operaattori.
disjunktion statementissa käytetään tai on inclusive. Se tarkoittaa ”jompaakumpaa” tai molempia.,
OR-tai loogisen disjunktion operaattorin edustamiseen käytetty symboli on \color{red}\Large{ \vee }. Se muistuttaa aakkosten v-kirjainta.
Kaksi propositioita P ja Q liittynyt TAI operaattori muodostaa yhdisteen lausunto on kirjoitettu seuraavasti:
\large{P \vee Q}.
{S \vee Q} luetaan ”P tai Q”
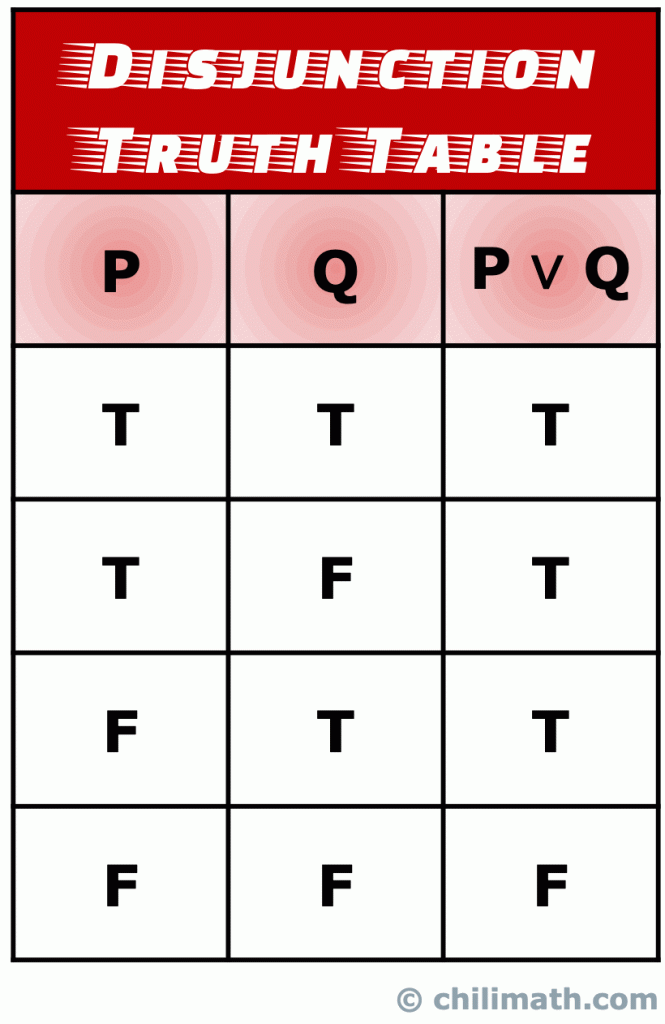
Muista: totuus, arvo yhdistelmälause P \vee Q on tosi, jos totuus arvo joko kaksi yksinkertaisia lausuntoja, P ja Q on tosi., Moreso, p \vee Q on myös totta, kun sekä lauseiden P että Q totuusarvot ovat totta. Kuitenkin, vain aika irrottaminen lausunto P \vee Q on epätosi, tapahtuu, kun totuus arvot sekä P ja Q ovat vääriä.
IV. Totuus Taulukko Looginen sisältö
implisiittisesti (tunnetaan myös nimellä ehdollinen lausunto) on eräänlainen yhdiste lausunto, joka on muodostettu yhdistämällä kaksi yksinkertaisia lausuntoja looginen seuraus sidekudoksen tai operaattori.,
loogisen implisiittioperaattorin edustamiseen käytettävä symboli on oikealle osoittava nuoli, siis oikealle osoittava nuoli.

Kun kaksi yksinkertaisia lausuntoja, P ja Q ovat liittyneet epäsuorasti toimija, meillä on:
\Large{P \Q}.
- missä P on tunnettu hypoteesi
- missä K on tunnettu johtopäätös
On monia tapoja, miten lukea ehdollinen {P \Q}., Alla muutamia yleisiä.
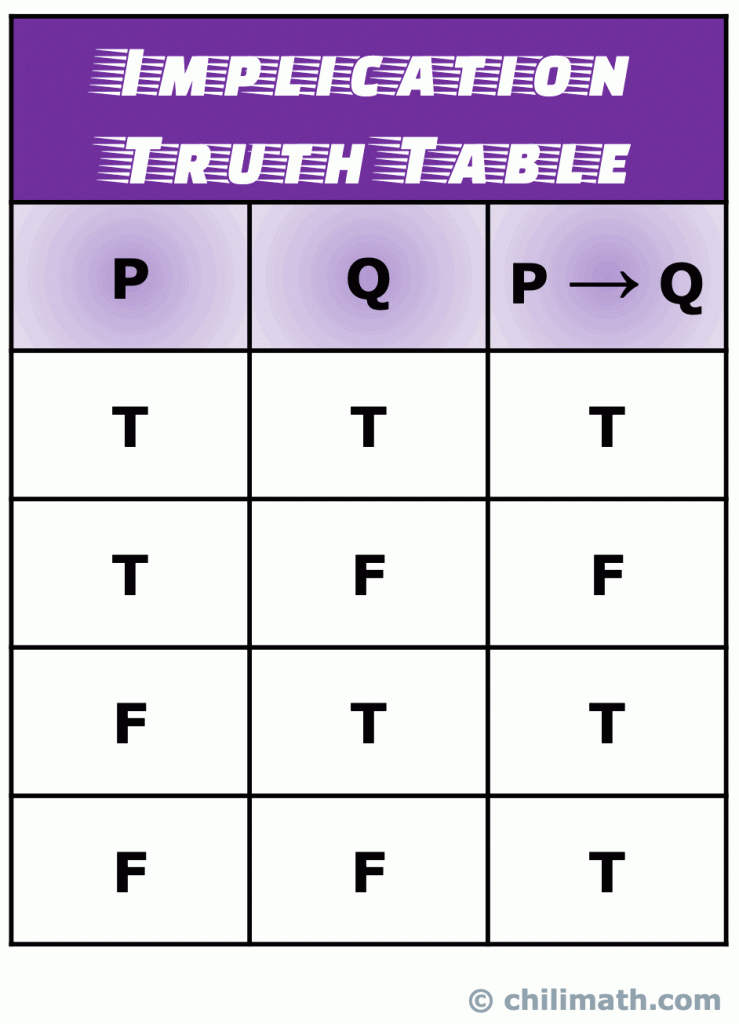
muista: yhdistetyn lausekkeen P \ – Q totuusarvo on totta, kun sekä yksinkertaiset lausumat P että Q ovat totta. Moreso, p \to Q on aina totta, jos P on väärä. Ainoa skenaario, että p \ – Q on väärä tapahtuu, kun P on totta, ja Q on väärä.
V., Totuus Taulukko Looginen Biconditional tai kahden Hengen Vaikutuksia
kaksinkertainen vaikutuksia (tunnetaan myös nimellä biconditional statement) on eräänlainen yhdiste lausunto, joka on muodostettu yhdistämällä kaksi yksinkertaisia lausumia kanssa biconditional operaattori. Biconditional statement on todella yhdistelmä ehdollinen lausuma ja sen converse.
kaksikotinen toimija merkitään kaksipäisellä nuolella.,

Kun liityt kaksi yksinkertaisia lausumia (tunnetaan myös nimellä molekyyli-lausunnot) ja biconditional operaattori, saamme:
\Large{P \leftrightarrow Q}
{S \leftrightarrow Q} luetaan ”P jos ja vain jos Q.,”
- missä P on tunnettu edeltäjä
- missä K on tunnettu seurauksena
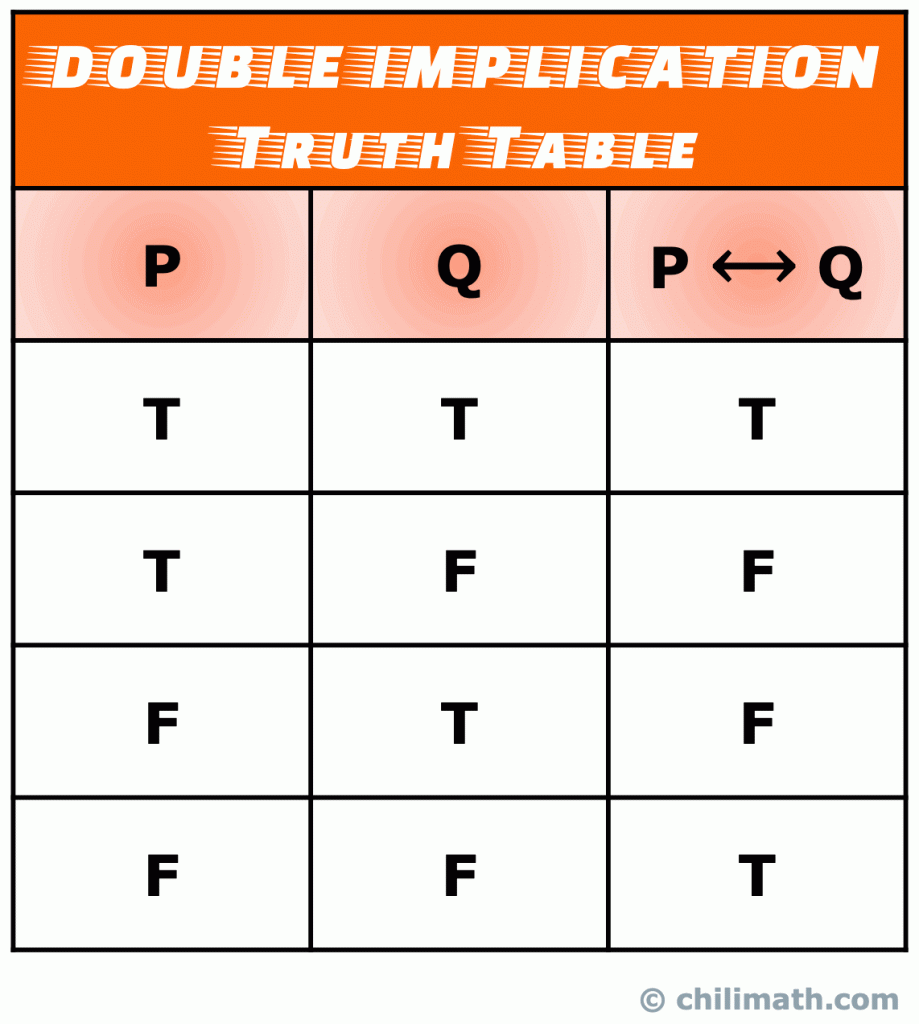
Muista: totuus, arvo biconditional lausunto P \leftrightarrow Q on tosi, kun sekä yksinkertaisia lausumia P ja Q ovat molemmat tosia tai molemmat epätosia. Muuten P \leftrightarrow Q on väärä.
saatat olla kiinnostunut myös:
Johdatus Totuus Taulukoita, Lausunnot, ja Looginen Connectives
Keskustella, Käänteinen, ja Contrapositive Ehdollinen Lausunto
Vastaa