Le déterminant d’une matrice est un numéro spécial qui peut être calculée à partir d’une matrice carrée.
Une Matrice est un tableau de nombres:
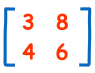
Matrice
(Ce qu’on a 2 Lignes et 2 Colonnes)
Le facteur déterminant de cette matrice est (les calculs sont expliqués plus loin):
à Quoi sert-il?
Le déterminant nous aide à trouver l’inverse d’une matrice, nous dit des choses sur la matrice qui sont utiles dans les systèmes d’équations linéaires, de calcul et plus encore.,
symbole
le symbole du déterminant est deux lignes verticales de chaque côté.
Exemple:
|A| désigne le déterminant de la matrice A
(Exactement le même symbole que la valeur absolue.)
calcul du déterminant
tout d’abord, la matrice doit être carrée (c’est-à-dire avoir le même nombre de lignes que de colonnes). Ensuite, ce n’est que de l’arithmétique de base., remember when you think of a cross:
- Blue is positive (+ad),
- Red is negative (−bc)
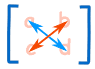
Example:
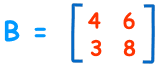
For a 3×3 Matrix
For a 3×3 matrix (3 rows and 3 columns):
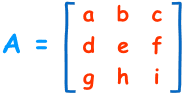
The determinant is:
|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
« The determinant of A equals .,.. etc »
Cela peut sembler compliqué, mais il y a un motif:
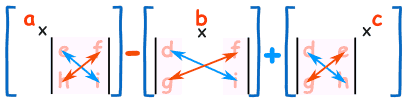
Pour déterminer le déterminant d’une matrice 3×3:
- Multipliez a par le déterminant de la matrice 2×2 qui n’est pas dans la ligne ou la colonne de a.
- de Même pour b, et c
- les résumer, mais n’oubliez pas le signe moins devant le b
en tant Que formule (rappelez-vous les barres verticales || signifie « déterminant »):
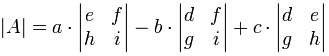
« Le déterminant de A est égal à une fois le facteur déterminant …,
Pour les matrices 4×4 et supérieures
Le motif continue pour les matrices 4×4:
- plus a fois le déterminant de la matrice qui n’est pas dans la ligne ou la colonne de a,
- moins b fois le déterminant de la matrice qui la matrice qui n’est pas dans la ligne ou la colonne de c,
- moins d fois le déterminant de la matrice qui n’est pas dans la ligne ou la colonne de d,

En tant que formule:
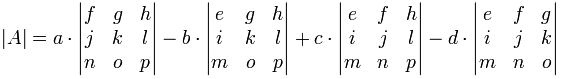
.,.. – b… +C… – d…). Ceci est important à retenir.
Le motif continue pour les matrices 5×5 et plus. Généralement préférable d’utiliser une Matrice Calculatrice pour ceux!
Pas la seule façon
Cette méthode de calcul s’appelle l ‘ « expansion Laplace » et je l’aime parce que le motif est facile à retenir. Mais il existe d’autres méthodes (juste pour que vous le sachiez).,
Résumé
- Pour une matrice 2×2 le déterminant est ad – bc
- Pour une matrice 3×3 multipliez a par le déterminant de la matrice 2×2 qui n’est pas dans la ligne ou la colonne de a, de même pour b et c, mais rappelez-vous que b a un signe négatif!
- Le motif continue pour les matrices plus grandes: multipliez a par le déterminant de la matrice qui n’est pas dans la ligne ou la colonne de a, continuez comme ceci sur toute la ligne, mais souvenez − vous du motif+−+ -.
Laisser un commentaire