La Distribution Binomiale

« Bi » signifie « deux » (comme un vélo à deux roues) … … il s’agit donc de choses avec deux résultats.,

nous allons Lancer une Pièce de monnaie!

Lancer une pièce juste trois fois … quelle est la chance d’avoir deux têtes?,tr>

THH THT TTH TTT

Which outcomes do we want?,

« Deux Têtes » peuvent être dans n’importe quel ordre: « HHT », « THH » et « HTH » ont tous deux Têtes (et une queue).

Donc 3 des résultats produisent « Deux têtes ».

Quelle est la probabilité de chaque résultat?,ations sont (P signifie « Probabilité »):

• P(Trois Têtes) = P(HHH) = 1/8
• P(Deux Têtes) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Une Tête) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Zéro Têtes) = P(TTT) = 1/8

On peut écrire cela en des termes d’une Variable Aléatoire X = « Le nombre de Têtes de 3 lancers d’une pièce de monnaie »:

• P(X = 3) = 1/8
• P(X = 2) = 3/8
• P(X = 1) = 3/8
• P(X = 0) = 1/8

Et c’est à quoi il ressemble comme un graphique:

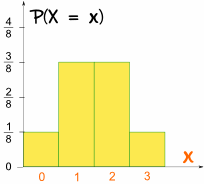
Il est symétrique!,

Faire une formule

Maintenant, imaginez que nous voulons les chances de 5 têtes en 9 lancers: énumérer tous les 512 résultats prendra beaucoup de temps!

Donc, nous allons faire une formule.

Dans notre exemple précédent, comment pouvons-nous obtenir les valeurs 1, 3, 3 et 1 ?

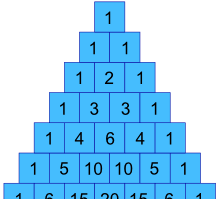
eh Bien, ils sont en fait dans le Triangle de Pascal !

Pouvons-nous les faire en utilisant une formule?

bien Sûr que nous pouvons, et c’est ici:

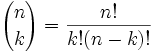
Il est souvent appelé « n choisir k »

• n = nombre total
• k = nombre nous voulons
• le « !, »signifie  » factoriel », par exemple 4! = 1×2×3×4 = 24

Vous pouvez en savoir plus à ce sujet sur Combinaisons et Permutations.

Essayons:

Utilisons-le pour une question plus difficile:

Bias!

Jusqu’à présent, les chances de succès ou d’échec étaient tout aussi probables.

Mais que se passe-t-il si les pièces sont biaisées (atterrissent plus d’un côté qu’un autre) ou si les choix ne sont pas 50/50.

nous allons dessiner un arbre schéma:

« Deux » le Poulet cas sont mis en évidence.

Les probabilités pour « deux poulets » sont toutes de 0,147, car nous multiplions deux 0,7 s et un 0,3 dans chaque cas. En d’autres mots

0.147 = 0.7 × 0.7 × 0.3

Ou, en utilisant des exposants:

= 0.72 × 0.31

L’objectif de 0,7 est la probabilité de chaque choix que nous voulons, appelons p

Le 2 est le nombre de choix que nous voulons, de l’appeler k

Et nous avons (pour l’instant):

= pk × 0.31

Le 0.,3 est la probabilité de l’autre choix, c’est donc: 1−p

Le 1 est le nombre de face de choix, il est donc: n−k

ce Qui nous donne:

= pk(1-p)(n-k)

Où

• p est la probabilité de chacun des choix que nous voulons
• k est le nombre de choix que nous voulons
• n est le nombre total de choix

Maintenant, nous savons que la probabilité de chaque résultat est 0.147

OK. C’était beaucoup de travail pour quelque chose que nous savions déjà, mais maintenant nous avons une formule que l’on peut utiliser pour une question plus difficile.,

montage

Maintenant que nous savons comment calculer combien d’:

n!k!(n-k)!

Et la probabilité de chaque:

pk(1-p)(n-k)

Lorsqu’il est multiplié ensemble, nous obtenons:

Important:

• Les essais sont indépendants,
• Il y a seulement deux résultats possibles à chaque essai,
• La probabilité de « succès » à chaque essai est constante.,

Quinconce

Avoir un jeu avec le Quinconce (puis lire en Quinconce Expliqué) pour voir la Distribution Binomiale dans l’action.

Lancer le dé

juste Un dé est jeté à quatre reprises. Calculer les probabilités d’obtenir:

• 0 Deux
• 1 Deux
• 2 Deux
• 3 Deux
• 4 Deux

Dans ce cas n=4, p = P(Deux) = 1/6

X est la Variable Aléatoire  » Nombre de Deux, de quatre lancers’.,

Remplacer x = 0 à 4 dans la formule:

P(k de n) = n!k!(n-k)! pk(1-p)(n-k)

Comme ceci (à 4 décimales):

Cette fois, le graphique n’est pas symétrique:

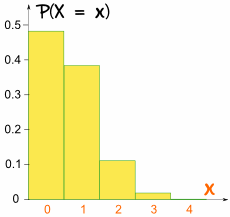
Il n’est pas symétrique!

Il est biaisée parce que p n’est pas 0.5

Sports Motos

Votre entreprise fait des motos sportives. 90% passent l’inspection finale (et 10% échouent et doivent être corrigés).

Quelle est la moyenne et la variance attendues des 4 prochaines inspections?

Tout d’abord, calculons toutes les probabilités.,

• n = 4,
• p = P(réussite) = 0.9

X est la Variable Aléatoire « Nombre de passes de quatre inspections ».

Remplacer x = 0 à 4 dans la formule:

P(k de n) = n!k!(n-k)! pk (1-p) (n-k)

Moyenne, Variance et Écart type

Calculons la Moyenne, la Variance et l’Écart type pour les inspections de vélo de Sport.

Il existe des formules (relativement) simples pour eux. Ils sont un peu difficiles à prouver, mais ils fonctionnent!,

La moyenne, ou de la « valeur attendue », est la suivante:

μ = np

La formule de la Variance est:

la Variance: σ2 = np(1-p)

Et l’Écart-type est la racine carrée de la variance:

σ = √(np(1-p))