Le Théorème de Pythagore

L’une des formules mathématiques les plus connues est le Théorème de Pythagore, qui nous fournit la relation entre les côtés d’un triangle rectangle. Un triangle rectangle se compose de deux jambes et d’une hypoténuse. Les deux jambes de répondre à un angle de 90° et l’hypoténuse est le côté le plus long du triangle rectangle et est le côté opposé à l’angle droit.,

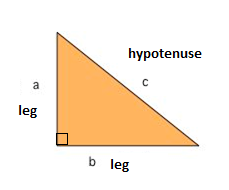
Le Théorème de Pythagore nous dit que la relation dans chaque triangle est:

$$a^{2}+b^{2}=c^{2}$$

Exemple

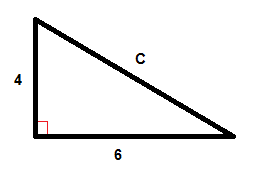
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\approx 7.2$$

Il ya un couple de types particuliers de droit des triangles, comme l’45°-45° triangles rectangles et les 30°-60° à droite du triangle.,

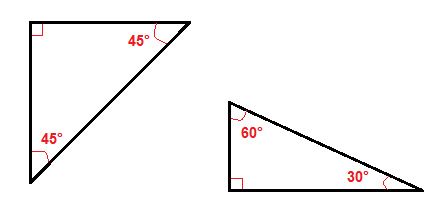
en Raison de leurs angles, il est plus facile de trouver l’hypoténuse ou les jambes dans ces triangles rectangles que dans tous les autres triangles rectangles.

Dans un triangle rectangle de 45°à 45°, il suffit de multiplier une jambe par √2 pour obtenir la longueur de l’hypoténuse.

Exemple

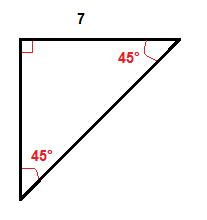
Nous multiplier la longueur de la jambe qui est de 7 pouces par √2 pour obtenir la longueur de l’hypoténuse.

$ $ 7\cdot \sqrt{2}\environ 9.,9 <

Dans un triangle rectangle de 30°à 60°, nous pouvons trouver la longueur de la jambe opposée à l’angle de 30° en utilisant cette formule:

$ $ a=\frac{1}{2}\cdot c c

Exemple

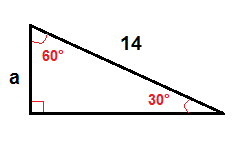
Pour trouver a, nous utilisons la formule ci-dessus.

$$a=\frac{1}{2}\cdot 14$$

$$a=7$$

la Vidéo de la leçon

Trouver les côtés de ce triangle rectangle