Ligne budgétaire: Notes sur la ligne budgétaire, L’espace, les changements et la pente

la connaissance du concept de ligne budgétaire ou de ce qu’on appelle aussi la contrainte budgétaire est essentielle pour comprendre la théorie de l’équilibre du consommateur.

Une courbe d’indifférence plus élevée montre un niveau de satisfaction plus élevé qu’une courbe inférieure. Par conséquent, un consommateur dans sa tentative de maximiser sa satisfaction tentera d’atteindre la courbe d’indifférence la plus élevée possible.,

Mais dans sa quête d’acheter de plus en plus de biens et d’obtenir ainsi de plus en plus de satisfaction, il doit travailler sous deux contraintes: premièrement, il doit payer les prix des biens et, deuxièmement, il a un revenu monétaire limité avec lequel acheter les biens. Ainsi, jusqu’où il irait pour ses achats dépend du prix des marchandises et du revenu monétaire qu’il doit dépenser pour les marchandises.,

pour expliquer l’équilibre du consommateur, il est également nécessaire d’introduire dans l’analyse de la courbe d’indifférence la ligne budgétaire qui représente les prix des biens et les revenus monétaires du consommateur.

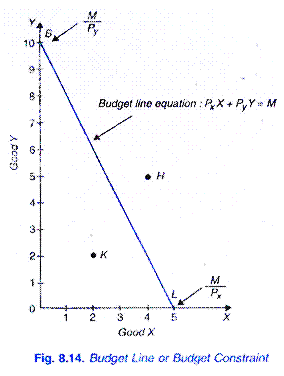
Supposons que notre consommation a obtenu des revenus de Rs. 50 à dépenser sur deux biens X et Y. que le prix du bien X Sur le marché soit Rs. 10 par unité et celle de Y Rs. 5 par unité. Si le consommateur dépense tout son revenu de Rs. 50 sur un bon X, il achèterait 5 unités de X; s’il dépense tout son revenu de Rs., 50 sur bon Y il achèterait 10 unités de Y. Si une ligne droite joignant 5Xand 10vis tiré, nous obtiendrons ce qu’on appelle la ligne de prix ou la ligne budgétaire.

ainsi, la ligne budgétaire montre toutes les combinaisons de deux biens que le consommateur peut acheter en dépensant son revenu monétaire donné sur les deux biens à leurs prix donnés. Un coup d’oeil à la Fig. 8.14 montre qu’avec Rs. 50 et les prix de X et Y étant Rs 10 et Rs. 5 respectivement le consommateur peut acheter l0Y et OX, ou Stand IX; ou 6Y et 2X,ou 4y et 3X etc.,

En d’autres termes, il peut acheter n’importe quelle combinaison qui se trouve sur la ligne budgétaire avec son revenu d’argent donné et les prix donnés des marchandises. Il convient de noter soigneusement que toute combinaison des deux biens tels que H (5Y et 4X) qui se trouve au-dessus et en dehors de la ligne budgétaire donnée sera hors de portée du consommateur.

Mais toute combinaison située dans la ligne budgétaire telle que K (2X et 2Y) sera bien à la portée du consommateur, mais s’il achète une telle combinaison, il ne dépensera pas tous ses revenus de Rs. 50., Ainsi, en supposant que la totalité du revenu donné est dépensée pour les biens donnés et à des prix donnés de ceux-ci, le consommateur doit choisir parmi toutes les combinaisons qui se trouvent sur la ligne budgétaire.

Il est clair d’en haut que la ligne budgétaire montre graphiquement la contrainte budgétaire. Les combinaisons de produits situées à droite de la ligne budgétaire sont inaccessibles car le revenu du consommateur n’est pas suffisant pour acheter ces combinaisons., Compte tenu du consommateur, des revenus et des prix des deux biens, les combinaisons de produits couché à gauche de la ligne budgétaire sont réalisables, que le consommateur peut acheter un quelconque d’entre eux.

Il est également important de se rappeler que L’interception OB sur l’axe Y De La Fig. 8.14 est égal au montant de la totalité de son revenu (M) divisé par le prix (PY) de la marchandise Y. C’est-à-dire OB = M/PY. De même, L’ordonnée à l’origine OL sur l’axe des abscisses mesure le revenu total divisé par le prix de la marchandise X. Ainsi OL = M/Px.,

la ligne budgétaire peut être écrite algébriquement comme suit:

où Px et Py désignent les prix des biens X et Y respectivement et M représente le revenu monétaire:

la ligne budgétaire ci-dessus l’équation (1) implique que, compte tenu du revenu monétaire du consommateur et des prix des deux biens, chaque combinaison figurant sur la ligne budgétaire coûtera la même somme D’argent et pourra donc être achetée avec le revenu donné., La ligne budgétaire peut être définie comme un ensemble de combinaisons de deux produits qui peuvent être achetés si la totalité du revenu donné est dépensée pour eux et sa pente est égale au négatif du rapport des prix.

espace budgétaire:

il faut bien comprendre que L’équation budgétaire PxX + PyY= m ou Y = M/Py – px / PyX représentée par la ligne budgétaire de la Fig. 8.14 décrit uniquement la ligne budgétaire et non l’espace budgétaire., Un espace budgétaire montre un ensemble de toutes les combinaisons des deux produits qui peuvent être achetés en dépensant la totalité ou une partie du revenu donné.

en d’autres termes, l’espace budgétaire représente l’opportunité pour le consommateur, c’est-à-dire toutes les combinaisons de deux produits qu’il peut acheter, compte tenu de sa contrainte budgétaire. Ainsi, l’espace budgétaire implique l’ensemble de toutes les combinaisons de deux biens pour lesquels le revenu dépensé pour le bien X (c.-à-d. PxX et le revenu dépensé pour le bien Y (c.-À-D. PyY) ne doit pas dépasser le revenu monétaire donné.,

Par conséquent, nous pouvons exprimer algébriquement l’espace budgétaire sous la forme d’inégalité suivante:

PXX + PyY < M, ou M > PXX + PyY

l’espace budgétaire a été représenté graphiquement sur la Fig. 8.15 comme zone ombrée. L’espace budgétaire est l’ensemble de la zone délimitée par la ligne budgétaire BL et les deux axes.

changements de prix et changement de ligne budgétaire:

maintenant, qu’advient-il de la ligne budgétaire si les prix des biens changent ou les revenus changent., Prenons d’abord le cas des changements de prix des marchandises. Ceci est illustré dans la Fig. 8.16. Supposons que la ligne budgétaire au début soit BL, compte tenu de certains prix des biens X et Y et d’un certain revenu. Supposons que le prix de X baisse, le prix de Y et le revenu restent inchangés. Maintenant, avec un prix inférieur de X, le consommateur pourra acheter plus de quantité de X qu’auparavant avec son revenu donné.

soit au prix inférieur de X, le revenu donné achète OL’ de X qui est supérieur à OL., Étant donné que le prix de Y reste le même, il ne peut y avoir de changement dans la quantité achetée du bien Y avec le même revenu donné et, par conséquent, il n’y aura pas de changement dans le point B. Ainsi, avec la baisse du prix du bien X, le revenu monétaire du consommateur et le prix de Y restant constants, la ligne budgétaire se déplacera vers la droite vers la nouvelle position BL’.,

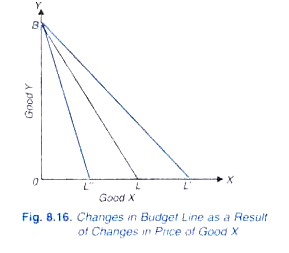
maintenant, qu’adviendra-t-il de la ligne budgétaire (ligne budgétaire initiale BL) si le prix du bien x augmente, le prix de bon y et revenu restant inchangé. Avec un prix plus élevé du bien X, le consommateur peut acheter une plus petite quantité de X, disons OL” qu’auparavant. Ainsi, avec la hausse du prix de X, la ligne budgétaire se déplacera vers la gauche vers la nouvelle position BL ».

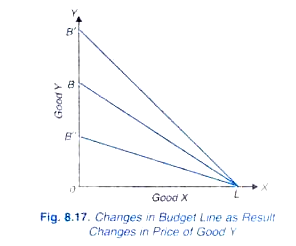
la Figure 8.,17 montre les changements dans la ligne budgétaire lorsque le prix du bien Y baisse ou augmente, le prix de X et le revenu restant les mêmes. En cela, la ligne budgétaire initiale est BL. Avec la chute du prix du bien Y, d’autres choses restant inchangées, le consommateur pourrait acheter plus de Y avec le revenu monétaire donné et donc la ligne budgétaire passera au-dessus de LB’. De même, avec la hausse du prix de Y, d’autres choses étant constantes, la ligne budgétaire passera en dessous de LB « .,

changements de revenus et changements de ligne budgétaire:

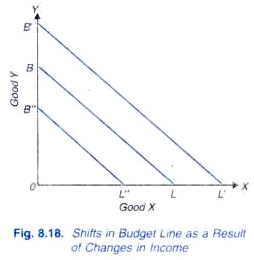
maintenant, la question Est de savoir ce qui arrive à la ligne budgétaire si les revenus changent, alors que les prix des marchandises restent les mêmes. L’effet des variations des recettes sur la ligne budgétaire est illustré à la Fig. 8.18. Soit BL la ligne budgétaire initiale, compte tenu de certains prix des biens et des revenus. Si le revenu du consommateur augmente alors que les prix des biens X et y restent inchangés, la ligne de prix se déplace vers le haut (disons, à BL’) et est parallèle à la ligne budgétaire initiale BL.,

en effet, avec l’augmentation du revenu, le consommateur est en mesure d’acheter une quantité proportionnellement plus grande de produit X qu’auparavant si la totalité du revenu est dépensée pour X, et une quantité proportionnellement plus grande de produit Y qu’auparavant si la totalité du revenu est dépensée pour Y. d’autre part, si le revenu du consommateur diminue, les prix des biens X et Y restant inchangés, la ligne budgétaire se déplace vers le bas (disons, à B”L”) mais reste parallèle à la ligne de prix initiale BL.,

c’est parce qu’un revenu inférieur achètera une quantité proportionnellement plus petite de produit X si la totalité du revenu est dépensée pour X et une quantité proportionnellement plus petite de produit Y si la totalité du revenu est dépensée pour Y.

il est clair d’en haut que la ligne budgétaire changera si les prix des biens changent ou si le revenu du consommateur change.

Ainsi, les deux déterminants de la ligne budgétaire sont:

(a) Les prix des marchandises, et

(b) Le consommateur est revenu pour être dépensés sur la marchandise.,

Pente de la Ligne Budgétaire et les Prix des Deux Biens:

Il est également important de se rappeler que la pente de la ligne budgétaire est égal au rapport des prix des deux biens. Cela peut être prouvé à l’aide de la Fig. 8.14. Supposons que le revenu donné du consommateur soit M et que les prix donnés des biens X et Y soient respectivement Px et Py.

la pente de la ligne budgétaire BL est OB/OL. Nous avons l’intention de prouver que cette pente est égal au rapport des prix des biens X et Y.,

la quantité de bien x achetée si la totalité du revenu donné M Y est dépensée est OL. Par conséquent, OL x Px = m

OL = m/Px

maintenant, la quantité de bien y acheté si la totalité du revenu donné M Y est dépensée est OB.

Il est ainsi prouvé que la pente de la ligne budgétaire BL est égal au rapport des prix des deux biens.