statistiques bayésiennes expliquées aux débutants en anglais Simple

aperçu

• Les inconvénients des statistiques fréquentistes conduisent à la nécessité de statistiques bayésiennes
• découvrez les statistiques bayésiennes et L’inférence bayésienne
• Il existe différentes méthodes pour tester la signification du modèle comme la valeur p, l’intervalle de confiance, etc

Introduction

les statistiques bayésiennes restent incompréhensibles dans l’esprit enflammé de nombreux analystes., Surpris par l’incroyable puissance de l’apprentissage automatique, beaucoup d’entre nous sont devenus infidèles aux statistiques. Notre objectif s’est réduit à l’exploration de l’apprentissage automatique. N’est-il pas vrai?

Nous ne comprenons pas que l’apprentissage automatique n’est pas le seul moyen de résoudre les problèmes du monde réel. Dans plusieurs situations, cela ne nous aide pas à résoudre des problèmes commerciaux, même si des données sont impliquées dans ces problèmes. Pour le moins, la connaissance des statistiques vous permettra de travailler sur des problèmes analytiques complexes, quelle que soit la taille des données.,

dans les années 1770, Thomas Bayes introduit le ‘théorème de Bayes’. Même après des siècles plus tard, l’importance des « statistiques bayésiennes » n’a pas disparu. En fait, aujourd’hui, ce sujet est enseigné dans de grandes profondeurs dans certaines des principales universités du monde.

avec cette idée, j’ai créé ce guide du débutant sur les statistiques bayésiennes. J’ai essayé d’expliquer les concepts de manière simpliste avec des exemples. Une connaissance préalable des statistiques de probabilité de base & est souhaitable., Vous devriez consulter ce cours pour obtenir un aperçu complet des statistiques et des probabilités.

à la fin de cet article, vous aurez une compréhension concrète de la Statistique Bayésienne et de ses concepts.,> Théorème de Bayes

inférence bayésienne

• fonction de probabilité de Bernoulli
• Distribution de croyance antérieure
• Distribution de croyance postérieure

Test de Signification – fréquentiste vs bayésien

• valeur p
• intervalles de confiance
• facteur de Bayes
• Intervalle de haute densité (IDH)

avant de nous plonger dans les statistiques bayésiennes, passons quelques minutes à comprendre les statistiques fréquentistes, la version la plus populaire des statistiques que la plupart D’entre nous rencontrent et les problèmes inhérents à cela.,

Statistiques fréquentistes

Le débat entre fréquentiste et bayésien hante les débutants depuis des siècles. Par conséquent, il est important de comprendre la différence entre les deux et comment il existe une mince ligne de démarcation!

C’est la technique inférentielle la plus utilisée dans le monde statistique. En fait, c’est généralement la première école de pensée qu’une personne entrant dans le monde de la statistique rencontre.

Les statistiques fréquentistes testent si un événement (hypothèse) se produit ou non., Il calcule la probabilité d’un événement à long terme de l’expérience (j’.e l’expérience est répétée dans les mêmes conditions pour l’obtention du résultat).

Ici, les distributions d’échantillonnage de taille fixe sont prises. Ensuite, l’expérience est théoriquement répétée un nombre infini de fois, mais pratiquement fait avec une intention d’arrêt. Par exemple, j’effectue une expérience avec une intention d’arrêt à l’esprit que j’arrêterai l’expérience lorsqu’elle sera répétée 1000 fois ou que je verrai un minimum de 300 têtes dans un lancer de pièce.

Allons plus loin maintenant.,

maintenant, nous allons comprendre les statistiques fréquentistes en utilisant un exemple de lancer de pièces. L’objectif est d’estimer l’équité de la pièce. Voici un tableau représentant la fréquence des têtes:

Nous savons que la probabilité d’obtenir une tête en lançant une pièce de monnaie équitable est de 0,5. No. of heads représente le nombre réel de têtes obtenues. Difference est la différence entre 0.5*(No. of tosses) - no. of heads.,

il est important de noter que, bien que la différence entre le nombre réel de têtes et le nombre attendu de têtes( 50% du nombre de lancers) augmente à mesure que le nombre de lancers augmente, la proportion du nombre de têtes par rapport au nombre total de lancers approche 0,5 (pour une pièce équitable).

cette expérience nous présente un défaut très commun trouvé dans l’approche fréquentiste à savoir la dépendance du résultat d’une expérience sur le nombre de fois que l’expérience est répétée.,

Pour en savoir plus sur les méthodes statistiques fréquentistes, vous pouvez vous diriger vers cet excellent cours sur les statistiques inférentielles.

Les défauts inhérents aux statistiques fréquentistes

Jusqu’ici, nous n’avons vu qu’un seul défaut dans les statistiques fréquentistes. Eh bien, c’est juste le début.

le 20ème siècle a vu une recrudescence massive des statistiques fréquentistes appliquées aux modèles numériques pour vérifier si un échantillon est différent de l’autre, un paramètre est suffisamment important pour être conservé dans le modèle et various other manifestations of hypothesis testing., Mais la statistique fréquentiste a souffert de grands défauts dans sa conception et son interprétation qui ont posé une grave préoccupation dans tous les problèmes de la vie réelle. Par exemple:

p-values mesuré par rapport à une statistique d’échantillon (taille fixe) avec certains changements d’intention d’arrêt avec changement d’intention et de taille d’échantillon. c’est-à-dire que si deux personnes travaillent sur les mêmes données et ont une intention d’arrêt différente, elles peuvent obtenir deux p- values différents pour les mêmes données, ce qui n’est pas souhaitable.,

Par exemple: La personne A peut choisir d’arrêter de lancer une pièce lorsque le nombre total atteint 100 tandis que B s’arrête à 1000. Pour différentes tailles d’échantillon, nous obtenons différents scores t et différentes valeurs p. De même, l’intention d’arrêter peut passer du nombre fixe de retournements à la durée totale du retournement. Dans ce cas aussi, nous sommes tenus d’obtenir différentes valeurs p.

2 – Intervalle de Confiance (C. I) comme p-value dépend fortement de la taille de l’échantillon., Cela rend le potentiel d’arrêt absolument absurde car quel que soit le nombre de personnes effectuant les tests sur les mêmes données, les résultats doivent être cohérents.

3 – les intervalles de confiance (C. I) ne sont pas des distributions de probabilité, ils ne fournissent donc pas la valeur la plus probable pour un paramètre et les valeurs les plus probables.

ces trois raisons sont suffisantes pour vous faire réfléchir aux inconvénients de l’approche fréquentiste et pourquoi une approche bayésienne est-elle nécessaire? Nous allons le découvrir.,

À partir de là, nous allons d’abord comprendre les bases de la statistique bayésienne.

Statistiques bayésiennes

« La statistique bayésienne est une procédure mathématique qui applique les probabilités à des problèmes statistiques. Il fournit aux gens les outils pour mettre à jour leurs croyances dans la preuve de nouvelles données.”

Vous avez obtenu cela? Permettez-moi de l’expliquer avec un exemple:

Supposons que sur les 4 courses du championnat (F1) entre Niki Lauda et James hunt, Niki a gagné 3 fois alors que James n’en a réussi que 1.,

Donc, si vous pariez sur le vainqueur de la prochaine course, qui serait-il ?

je parie que vous diriez Niki Lauda.

Voici la torsion. Et si on vous dit qu’il a plu une fois quand James a gagné et une fois quand Niki a gagné et qu’il est certain qu’il pleuvra à la prochaine date. Alors, sur qui parieriez-vous votre argent maintenant ?

Par intuition, il est facile de voir que les chances de gagner pour James ont considérablement augmenté. Mais la question est: combien ?,

pour comprendre le problème actuel, nous devons nous familiariser avec certains concepts, dont le premier est la probabilité conditionnelle (expliquée ci-dessous).

En outre, il y a certains pré-requis:

Pré-Requis:

1. l’Algèbre Linéaire : Pour rafraîchir vos bases, vous pouvez consulter la Khan Academy Algèbre.
2. probabilité et statistiques de base: pour rafraîchir vos bases, vous pouvez consulter un autre cours de Khan Academy.

3.,1 Probabilité conditionnelle

Elle est définie comme la: Probabilité d’un événement A donné B est égal à la probabilité de B et A se produisant ensemble divisé par la probabilité de B.”

Par exemple: Supposons deux ensembles partiellement croisés A et B comme indiqué ci-dessous.

Définir Un représente un ensemble d’événements et l’Ensemble B représente un autre. Nous souhaitons calculer la probabilité qu’un B donné se soit déjà produit. Représentons l’événement B en l’ombrant de rouge.,

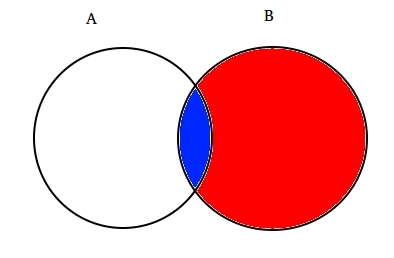
Maintenant, puisque B est arrivé, la partie qui, maintenant, pour Un est la partie ombrée en bleu qui est intéressant . Ainsi, la probabilité de B s’avère être:

par conséquent, on peut écrire la formule de l’évènement B donné Un a déjà eu lieu:

ou

Maintenant, la deuxième équation peut être réécrite comme :

Ceci est connu comme la Probabilité Conditionnelle.,

Essayons de répondre à un problème de paris avec cette technique.

Supposons que B soit le cas de victoire de James Hunt. Un cas de pluie. Par conséquent,

En substituant les valeurs dans la formule de probabilité conditionnelle, nous obtenons la probabilité d’être autour de 50%, ce qui est presque le double de 25% lorsque la pluie n’a pas été prise en compte (Résolvez-la à votre fin).

Cela a encore renforcé notre croyance en la victoire de James à la lumière de nouvelles preuves, à savoir la pluie., Vous devez vous demander que cette formule ressemble beaucoup à quelque chose dont vous avez peut-être beaucoup entendu parler. Réfléchis!

probablement, vous l’avez bien deviné. On dirait le théorème de Bayes.

Le théorème de Bayes est construit au-dessus de la probabilité conditionnelle et se trouve au cœur de L’inférence bayésienne. Il faut bien comprendre dans le détail maintenant.

3.2 théorème de Bayes

Le théorème de Bayes entre en vigueur lorsque plusieurs événements forment un ensemble exhaustif avec un autre événement B. Cela pourrait être compris à l’aide du diagramme ci-dessous.,

Maintenant, B peut être écrite sous la forme

Donc, la probabilité de B peut être écrite,

Mais

Donc, en remplaçant P(B) dans l’équation de la probabilité conditionnelle de nous get

C’est l’équation du Théorème de Bayes.

inférence bayésienne

il ne sert à rien de plonger dans l’aspect théorique de celle-ci. Donc, nous allons apprendre comment cela fonctionne!, Prenons un exemple de lancer de pièces de monnaie pour comprendre l’idée derrière l’inférence bayésienne.

Une partie importante de l’inférence bayésienne est l’établissement de paramètres et de modèles.

Modèles sont la formulation mathématique des événements observés. Les paramètres sont les facteurs des modèles affectant les données observées. Par exemple, lors du lancer d’une pièce, l’équité de la pièce peut être définie comme le paramètre de la pièce noté θ. Le résultat des événements peut être indiqué par D.

Répondez maintenant., Quelle est la probabilité de 4 têtes sur 9 lancers (D) Compte tenu de l’équité de coin (θ). j’.e P(D|θ)

Attendez, ai-je poser la bonne question? Aucun.

nous devrions être plus intéressés à savoir : Étant donné un résultat (D) Quelle est la probabilité que la pièce soit juste (θ=0.5)

représentons-la en utilisant le théorème de Bayes:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

ici, P(θ) est le précédent, c’est-à-dire la force de notre croyance en l’équité de la pièce avant le lancer., Il est parfaitement correct de croire que coin peut avoir n’importe quel degré d’équité entre 0 et 1.

P(D|θ) est la probabilité d’observer notre résultat compte tenu de notre réseau de distribution pour θ. Si nous savions que la pièce était juste, cela donne la probabilité d’observer le nombre de têtes dans un nombre particulier de flips.

P(D) est la preuve. Il s’agit de la probabilité de données déterminée par la somme (ou l’intégration) de toutes les valeurs possibles de θ, pondérée par la force avec laquelle nous croyons en ces valeurs particulières de θ.,

si nous avions plusieurs vues sur l’équité de la pièce (mais que nous ne le savions pas avec certitude), cela nous indique la probabilité de voir une certaine séquence de retournements pour toutes les possibilités de notre croyance en l’équité de la pièce.

P(θ|D) est la croyance postérieure de nos paramètres après avoir observé la preuve, c’est-à-dire le nombre de têtes.

à partir de là, nous allons approfondir les implications mathématiques de ce concept. Ne vous inquiétez pas. Une fois que vous les comprenez, se rendre à ses mathématiques est assez facile.,

pour définir correctement Notre modèle , nous avons besoin de deux modèles mathématiques avant la main. Un pour représenter la fonction de vraisemblance P(D|θ) et l’autre pour représenter la distribution des croyances antérieures . Le produit de ces deux donne la croyance postérieure p (θ|D) distribution.

étant donné que prior et posterior sont tous deux des croyances sur la distribution de l’équité de la pièce, l’intuition nous dit que les deux devraient avoir la même forme mathématique. Gardez cela à l’esprit. Nous reviendrons à nouveau.,

Il existe donc plusieurs fonctions qui soutiennent l’existence du théorème de bayes. Les connaître est important, c’est pourquoi je les ai expliqués en détail.

4.1. Bernoulli likelihood function

Récapitulons ce que nous avons appris sur la fonction de vraisemblance. Nous avons donc appris que:

C’est la probabilité d’observer un nombre particulier de têtes dans un nombre particulier de flips pour une équité de pièce donnée. Cela signifie que notre probabilité d’observer les têtes/queues dépend de l’équité de coin (θ).,

P(y=1|θ)=

P(y=0|θ)=

Il est intéressant de remarquer que représentant 1 en tant que chefs et 0 de la queue est juste une notation mathématique pour élaborer un modèle. Nous pouvons combiner les définitions mathématiques ci-dessus en une seule définition pour représenter la probabilité des deux résultats.

P(y/θ)=

C’est ce qu’on appelle la fonction de vraisemblance de Bernoulli et la tâche de retournement de pièces s’appelle les essais de Bernoulli.,

y={0,1},θ=(0,1)

Et, quand nous voulons voir une série de chefs ou de pirouettes, sa probabilité est donnée par:

en Outre, si nous nous intéressons à la probabilité du nombre de têtes z tourner dans le nombre N de lancers, alors la probabilité est donnée par:

4.2. Distribution des croyances antérieures

Cette distribution est utilisée pour représenter nos forces sur les croyances sur les paramètres en fonction de l’expérience précédente.,

Mais, si l’on n’a aucune expérience?

Ne vous inquiétez pas. Les mathématiciens ont également conçu des méthodes pour atténuer ce problème. Il est connu sous le nom uninformative priors. Je voudrais vous informer au préalable que ce n’est qu’un nom erroné. Chaque prior non informatif fournit toujours une information événement la distribution constante prior.

eh Bien, la fonction mathématique utilisée pour représenter les croyances antérieures est connu comme beta distribution., Il a de très belles propriétés mathématiques qui nous permettent de modéliser nos croyances sur une distribution binomiale.

fonction de densité de Probabilité de la distribution bêta est de la forme :

où, notre focus reste sur le numérateur. Le dénominateur est là juste pour s’assurer que la fonction de densité de probabilité totale lors de l’intégration est évaluée à 1.

α et β sont appelés la forme de décider des paramètres de la fonction de densité., Ici α est analogue à nombre de têtes dans les essais et β correspond au nombre de queues., Les diagrammes ci-dessous vous aideront à visualiser les distributions bêta pour différentes valeurs de α Et β

Vous pouvez également dessiner la distribution bêta pour vous-même en utilisant le code suivant dans R:

remarque: α Et β sont intuitifs à comprendre car ils peuvent être calculés en connaissant la moyenne (μ) et l’écart type (σ) de la distribution., En fait, ils sont liés comme suit:

Si la moyenne et l’écart type d’une distribution sont connus , les paramètres de forme peuvent être facilement calculés.

inférence tirée des graphiques ci-dessus:

1. quand il n’y avait pas de tirage au sort, nous pensions que toute équité de la pièce est possible comme représenté par la ligne plate.
2. Lorsqu’il y avait plus de têtes que de queues, le graphique montrait un pic décalé vers le côté droit, indiquant une probabilité plus élevée de têtes et cette pièce n’est pas juste.,
3. Au fur et à mesure que plus de lancers sont effectués et que les têtes continuent d’arriver en plus grande proportion, le pic se rétrécit, augmentant notre confiance dans l’équité de la valeur de la pièce.

4.3. Distribution de croyance postérieure

La raison pour laquelle nous avons choisi la croyance antérieure est d’obtenir une distribution bêta. En effet, lorsque nous la multiplions avec une fonction de vraisemblance, la distribution postérieure donne une forme similaire à la distribution antérieure qui est beaucoup plus facile à comprendre et à comprendre., Si cette quantité d’informations vous met en appétit, je suis sûr que vous êtes prêt à faire un kilomètre supplémentaire.

Calculons la croyance postérieure en utilisant le théorème de bayes.

le Calcul postérieur de la croyance à l’aide de Bayes le Théorème

Maintenant, notre postérieure croyance devient,

Ce qui est intéressant., Il suffit de connaître la distribution moyenne et standard de notre croyance sur le paramètre θ et en observant le nombre de têtes dans N flips, nous pouvons mettre à jour notre croyance sur le paramètre du modèle(θ).

Permet de comprendre avec l’aide d’un exemple simple:

Supposons que, vous pensez qu’une pièce est biaisée. Il a un biais moyen (μ) d’environ 0,6 avec un écart type de 0,1.

Alors ,

α= 13.8 , β=9.2

j’.,e notre distribution sera biaisée du côté droit. Supposons que vous ayez observé 80 têtes (z=80) en 100 flips (N=100). Nous allons voir comment notre accord préalable et postérieure sont les croyances d’aller le chercher:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

vous Permet de visualiser à la fois les croyances sur un graphique:

Les R du code du graphique ci-dessus:

}

alors Que de plus en plus de flips sont faites et les nouvelles données sont observées, nos croyances mise à jour., C’est le vrai pouvoir de L’inférence bayésienne.

Test de Signification – fréquentiste vs bayésien

sans entrer dans les structures mathématiques rigoureuses, cette section vous donnera un aperçu rapide des différentes approches des méthodes fréquentiste et bayésienne pour tester la signification et la différence entre les groupes et quelle méthode est la plus fiable.

5.1. p-value

dans ce cas, le score t pour un échantillon particulier à partir d’une distribution d’échantillonnage de taille fixe est calculé. Ensuite, les valeurs p sont prédites., Nous pouvons interpréter les valeurs p comme (en prenant un exemple de valeur p comme 0,02 pour une distribution de moyenne 100): Il y a 2% de probabilité que l’échantillon ait une moyenne égale à 100.

Cette interprétation souffre du défaut que pour des distributions d’échantillonnage de différentes tailles, on est obligé d’obtenir un score t différent et donc une valeur p différente. C’est complètement absurde. Une valeur p inférieure à 5% ne garantit pas que l’hypothèse nulle est fausse, ni une valeur p supérieure à 5% ne garantit que l’hypothèse nulle est juste.

5.2., Intervalles de confiance

les intervalles de confiance souffrent également du même défaut. De plus , puisque C. I n’est pas une distribution de probabilité, il n’y a aucun moyen de savoir quelles valeurs sont les plus probables.

5.3. Facteur de Bayes

le facteur de Bayes est l’équivalent de la valeur p dans le cadre bayésien. Permet de le comprendre de manière globale.

l’hypothèse nulle dans le cadre bayésien suppose ∞ distribution de probabilité seulement à une valeur particulière d’un paramètre (disons θ=0.5) et une probabilité nulle autre où., (M1)

L’hypothèse alternative est que toutes les valeurs de θ sont possibles, d’où une courbe plate représentant la distribution. (M2)

Maintenant, la distribution postérieure des nouvelles données ressemble à ci-dessous.

Les statistiques bayésiennes ont ajusté la crédibilité (probabilité) de diverses valeurs de θ. On peut facilement voir que la distribution de probabilité s’est déplacée vers M2 avec une valeur supérieure à M1, c’est-à-dire que M2 est plus susceptible de se produire.,

le facteur de Bayes ne dépend pas des valeurs de distribution réelles de θ mais de l’amplitude du décalage des valeurs de M1 et M2.

dans le panneau A (ci-dessus): la barre de gauche (M1) est la probabilité antérieure de l’hypothèse nulle.

dans le panneau B (illustré), la barre de gauche est la probabilité postérieure de l’hypothèse nulle.

Le facteur Bayes est défini comme le rapport entre les cotes postérieures et les cotes antérieures,

pour rejeter une hypothèse nulle, un BF < 1/10 est préféré.,

nous pouvons voir les avantages immédiats de l’utilisation du facteur Bayes au lieu des valeurs p car elles sont indépendantes des intentions et de la taille de l’échantillon.

5.4. Intervalle haute densité (IDH)

L’IDH est formé à partir de la distribution postérieure après observation des nouvelles données. Puisque L’IDH est une probabilité, l’IDH de 95% donne les valeurs les plus crédibles à 95%. Il est également garanti que les valeurs de 95% se situeront dans cet intervalle contrairement à C. i.

notez que l’IDH à 95% dans la distribution antérieure est plus large que la distribution postérieure à 95%., En effet, notre croyance en L’IDH augmente lorsque nous observons de nouvelles données.

notes de fin

le but de cet article était de vous faire réfléchir sur les différents types de philosophies statistiques et sur la façon dont aucune d’entre elles ne peut être utilisée dans toutes les situations.

il est grand temps que les deux philosophies soient fusionnées pour atténuer les problèmes du monde réel en s’attaquant aux défauts de l’autre., La deuxième partie de cette série se concentrera sur les techniques de réduction de la dimensionnalité utilisant les algorithmes MCMC (Markov Chain Monte Carlo). La partie III sera basée sur la création d’un modèle de régression bayésienne à partir de zéro et l’interprétation de ses résultats en R. Donc, avant de commencer avec la partie II, j’aimerais avoir vos suggestions / commentaires sur cet article.