dans cette leçon, nous allons construire les cinq (5) connectifs logiques communs ou opérateurs. Ils sont considérés comme des connectifs logiques communs car ils sont très populaires, utiles et toujours enseignés ensemble.
avant de commencer, je vous suggère de revoir mon autre leçon dans laquelle le lien est affiché ci-dessous.
cette leçon d’introduction sur les tables de vérité contient des connaissances ou des informations préalables qui vous aideront à mieux comprendre le contenu de cette leçon.,
Introduction aux Tables de vérité, aux instructions et aux Connectives
Les chiers commencent par lister les cinq (5) connectives logiques communes.
Les Cinq (5) Communes de Connecteurs Logiques ou des Opérateurs
- Négation Logique
- Conjonction Logique (ET)
- Disjonction Logique (Inclusive OU)
- Implication Logique (Conditionnel)
- Logique Biconditional (Double Implication)
I., Table de vérité de la négation logique
la négation d’une déclaration est également une déclaration avec une valeur de vérité qui est exactement opposée à celle de la déclaration originale. Par exemple, la négation de l’énoncé est écrit symboliquement comme
~\large{P} ou \large{\neg P}.
~{P} ou {\neg P} est lu comme « not P.”
rappelez-vous: L’opérateur de négation désigné par le symbole ~ or \neg prend la valeur de vérité de l’instruction d’origine puis produit l’exact opposé de sa valeur de vérité., En d’autres termes, la négation inverse simplement la valeur de vérité d’une déclaration donnée. Ainsi, si l’instruction P est vraie, alors la valeur de vérité de sa négation est fausse. De la même manière, si P est fausse la valeur de vérité de sa négation est vraie.

II. table de vérité de la conjonction logique
une conjonction est un type d’énoncé composé qui est composé de deux propositions (également connues sous le nom opérateur.,
le symbole utilisé pour représenter L’opérateur de conjonction ET OU logique est \color{red}\Large{\wedge}. Il ressemble à une inversion de la lettre V.
Si nous avons deux simples énoncés P et Q, et nous voulons former une instruction composée joints par l’opérateur ET, nous pouvons l’écrire:
\large{P \wedge Q}.
{P \wedge Q} est lu comme « P et Q.”
rappelez-vous: la valeur de vérité de l’instruction composée P \wedge Q n’est vraie que si les valeurs de vérité P et Q sont toutes les deux vraies., Sinon, P \ wedge Q est faux.
notez dans le tableau de vérité ci-dessous que lorsque P est vrai et Q est vrai, P \wedge Q est vrai. Cependant, les trois autres combinaisons de propositions P et Q sont fausses.

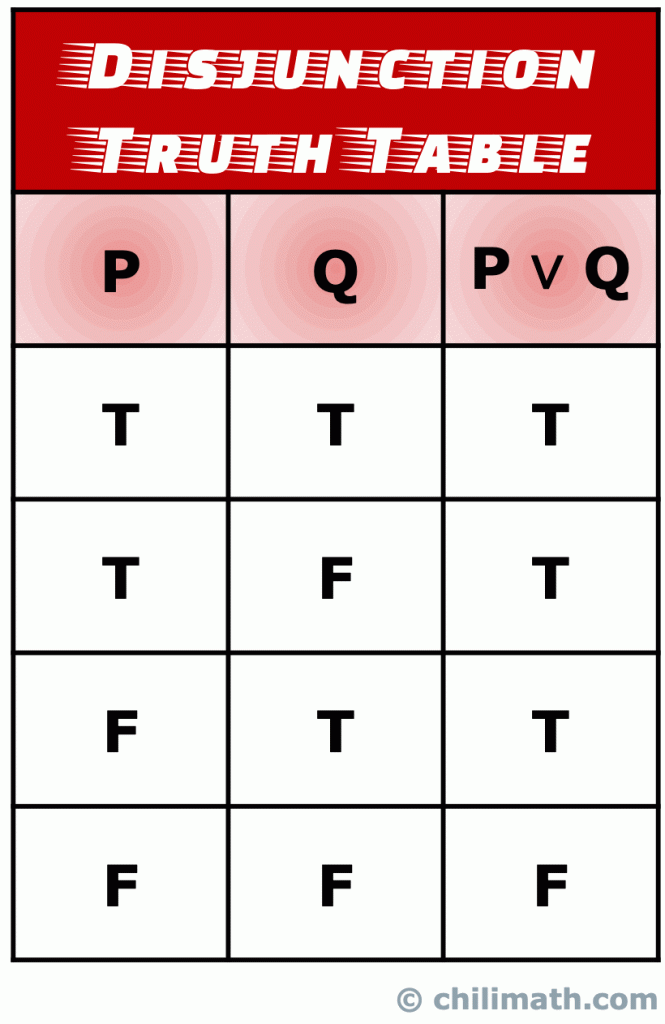
III. Table de vérité de la Disjonction Logique
Une disjonction est une sorte de composé de déclaration qui est composé de deux déclarations simples formé en joignant les énoncés avec l’opérateur OU.
dans une déclaration de disjonction, L’utilisation de ou EST inclusive. Que signifie « l’un ou l’autre”, ou les deux.,
le symbole utilisé pour représenter L’opérateur de disjonction OU OU logique est \color{red}\Large{ \vee }. Il ressemble à la lettre V de l’alphabet.
deux propositions P et Q jointes par l’opérateur OR pour former une instruction composée s’écrivent comme suit:
\large{P \Vee Q}.
{P \vee Q} est lu comme « P ou Q”.
Souvenez-vous: La valeur de vérité de l’instruction composée P \vee Q est vraie si la valeur de vérité de deux simples énoncés P et Q est vraie., De plus, P \ Vee Q est également vrai lorsque les valeurs de vérité des deux déclarations P et Q sont vraies. Cependant, la seule fois où L’instruction de disjonction P \ Vee Q est fausse, se produit lorsque les valeurs de vérité de P et Q sont fausses.
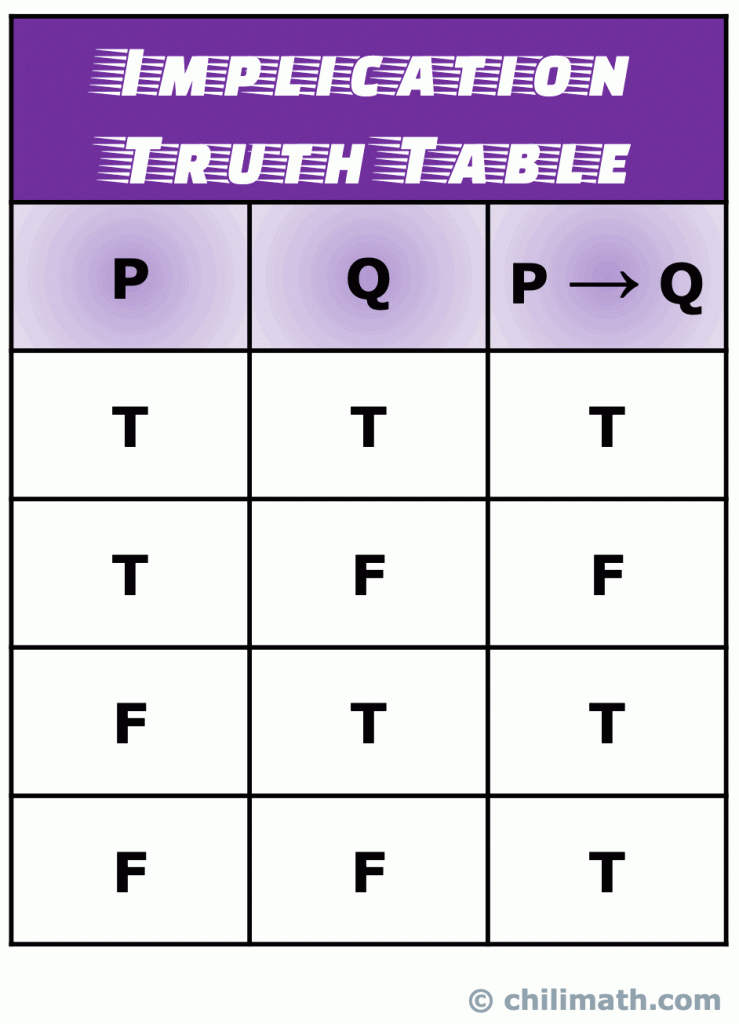
IV. table de vérité de L’Implication logique
une implication (également connue sous le nom d’instruction conditionnelle) est un type d’instruction composée qui est formée en joignant deux déclarations avec l’implication logique connective ou opérateur.,
le symbole utilisé pour représenter l’opérateur d’implication logique est une flèche pointant vers la droite, donc vers la droite.

Lorsque deux simples énoncés P et Q sont rejoints par l’implication de l’opérateur, nous avons:
\Large{P \Q}.
- où P est connu comme l’hypothèse
- où Q est connu comme la conclusion
Il existe de nombreuses façons de lire le conditionnel {P \Q}., Ci-dessous sont quelques-uns des plus communes.
rappelez-vous: la valeur de vérité de L’instruction composée P \À Q est vraie lorsque les deux instructions simples P et Q sont vraies. De plus, P \ À Q est toujours vrai si P est faux. Le seul scénario selon lequel P \À Q est faux se produit lorsque P est vrai et Q est faux.
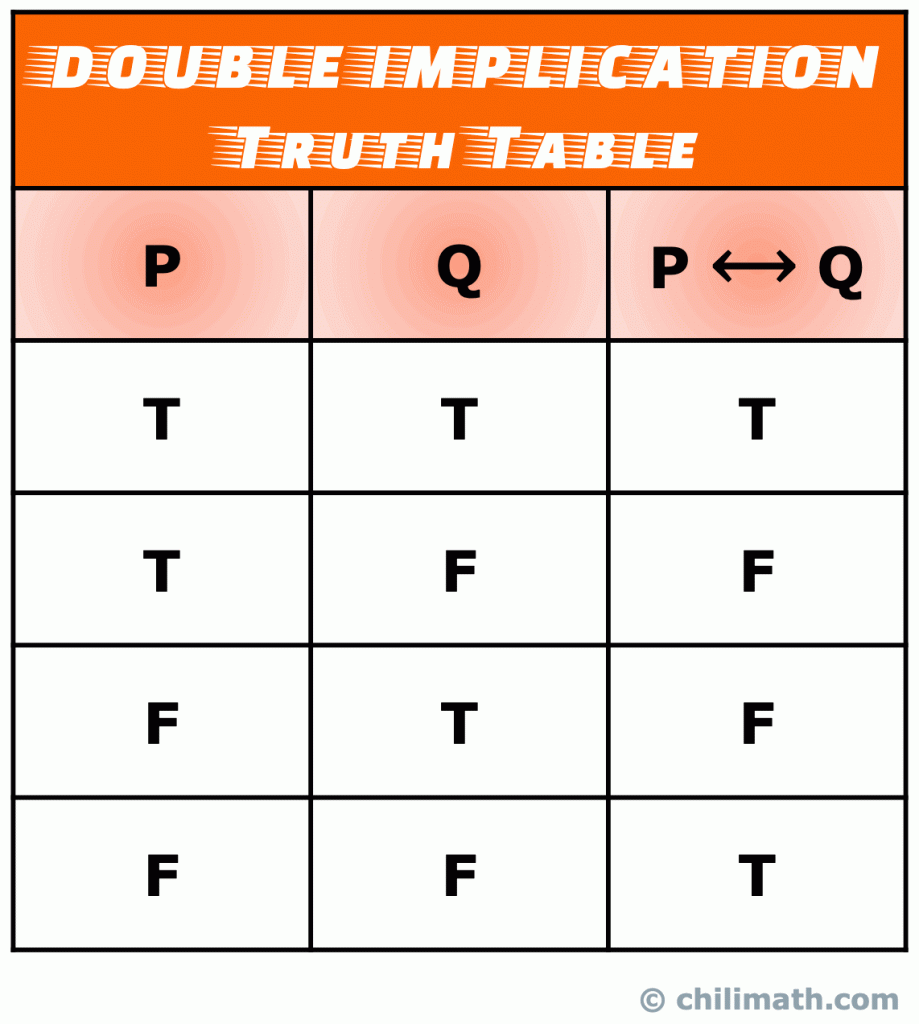
V., Table de vérité de L’Implication logique Biconditionnelle ou Double
Une double implication (également connue sous le nom d’instruction biconditionnelle) est un type d’instruction composée qui est formée en joignant deux instructions simples avec l’opérateur biconditionnel. Une déclaration biconditionnelle est vraiment une combinaison d’une déclaration conditionnelle et de son inverse.
l’opérateur biconditionnel est désigné par une flèche à double tête.,

Lorsque vous vous joignez à deux états (aussi connu comme moléculaires consolidés) avec le biconditional opérateur, nous obtenons:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} est lu comme « P si et seulement si Q.,”
- où P est connu comme l’antécédent
- où Q est connu comme la conséquence
Souvenez-vous: La valeur de vérité de l’biconditional déclaration de P \leftrightarrow Q est vraie lorsque les deux simples énoncés P et Q sont vraies ou fausses. Sinon, P \leftrightarrow Q est faux.
Vous pouvez aussi être intéressé par:
Introduction à la table de Vérité, de Déclarations et de Connecteurs Logiques
Converse, Inverse, et Contrapositive d’une Instruction Conditionnelle
Laisser un commentaire