|
” Bi “jelentése” két ” (mint egy kerékpárnak két kereke van) … |
 |

dobni egy Érmét:
- jutottunk Fej (H), vagy
- Írás (T)
mondjuk a valószínűsége annak, hogy az érme leszállás H ½
a valószínűsége annak, hogy az érme leszállás T ½
dobjunk fel egy Érmét!
Dobj egy tisztességes érmét háromszor … mi az esélye annak, hogy két fejet kapjunk?,tr>












Which outcomes do we want?,
a”két fej” bármilyen sorrendben lehet: “HHT”, “THH” és ” HTH ” mindegyiknek két feje van (és egy farka).
így 3 Az eredmények termelnek “két fej”.
mi az egyes eredmények valószínűsége?,ations vagy (P azt jelenti, hogy “Valószínűsége”):
- P(Három Fej) = P(nos, itt) = 1/8
- P(Két Fej) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Fej) = P(HTT) + P(THT) + P(FOGÁVAL) = 1/8 + 1/8 + 1/8 = 3/8
- P(Nulla Fej) = P(TTT) = 1/8
Tudjuk írni ezt a szempontból, hogy egy Véletlen Változó, X, a = “A száma Fejek 3 dobja egy érme”:
- P(X = 3) = 1/8
- P(X = 2) = 3/8
- P(X = 1) = 3/8
- P(X = 0) = 1/8
ez az, amit úgy néz ki, mint egy grafikon:
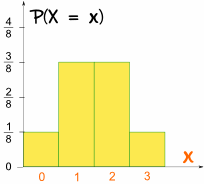
szimmetrikus!,
képlet készítése
most képzelje el, hogy az 5 fej esélyeit 9 dobásban akarjuk: az összes 512 eredmény felsorolása hosszú időt vesz igénybe!
tehát készítsünk egy képletet.
korábbi példánkban hogyan kaphatjuk meg az 1, 3, 3 és 1 értékeket ?
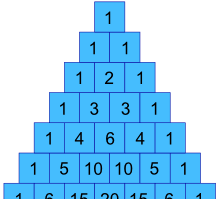
Nos, valójában Pascal háromszögében vannak !
készíthetjük őket egy képlet segítségével?
biztosan tudjuk, és itt van:
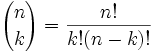
gyakran “n choose k”
- n = teljes szám
- k = szám, amit akarunk
- a “!,”azt jelenti, “faktoriális”, például 4! = 1×2×3×4 = 24
erről bővebben a kombinációk és permutációk oldalon olvashat.
próbáljuk ki:
használjuk egy nehezebb kérdésre:
elfogultság!
eddig a siker vagy kudarc esélyei egyaránt valószínűek voltak.
de mi van, ha az érmék elfogultak (az egyik oldalon több, mint a másik oldalon), vagy a választások nem 50/50.
példa: szendvicseket árul. Az emberek 70% – A választja a csirkét, a többiek valami mást választanak.
Ez pont olyan, mint a fej és a farok példa, de 70/30 helyett 50/50.,
rajzolunk egy fa diagramot:
a “két csirke” eset kiemelésre kerül.
a “két csirke” valószínűségei mind 0,147-esek, mert két 0,7-es és egy 0,3-as szorzatot osztunk minden esetben. Más szóval
0.147 = 0.7 × 0.7 × 0.3
vagy exponensek használatával:
= 0.72 × 0.31
A 0.7 minden választás valószínűsége, amit akarunk, nevezzük p
a 2 a kívánt választások száma, nevezzük k
és van (eddig):
= pk × 0.31
a 0.,3 az ellenkező választás valószínűsége, tehát: 1−p
az 1 az ellentétes választások száma, tehát: n−k
, amely megadja nekünk:
= pk(1-p)(n-k)
ahol
- P minden választás valószínűsége
- k a kívánt választások száma
- n a választás teljes száma választások
k
n
n
most már tudjuk, hogy az egyes eredmények valószínűsége 0,147
ok. Ez sok munka volt valami, amit már tudtunk, de most van egy képlet, amelyet keményebb kérdésekre használhatunk.,
összerakva
most már tudjuk, hogyan kell kiszámítani, hogy hány:
n!k!(n-k)!
és az egyes valószínűségek:
pk (1-p)(n-k)
együtt szorozva kapjuk:
valószínűsége k ki N módon:
P(k ki n) = n!k!(n-k)! pk (1-p)(n-k)
az Általános binomiális valószínűségi képlet
Fontos megjegyzések:
- a vizsgálatok függetlenek,
- minden kísérletben csak két lehetséges eredmény létezik,
- a “siker” valószínűsége állandó.,
Quincunx

játszanak a Quincunx (majd olvassa Quincunx magyarázata), hogy a binomiális eloszlás akcióban.
dobja a szerszámot
egy tisztességes szerszámot dobnak. Kiszámítja a valószínűsége, hogy:
- 0 Kettesével
- 1 Két
- 2 Kettesével
- 3 Kettesével
- 4 Kettesével
ebben Az esetben n=4, p = P(Két) = 1/6
X Véletlen Változó Számú Kettesével a négy dob’.,
helyettesítő x = 0-4 a képletbe:
P (k az n-ből) = n!k!(n-k)! Pk(1-p)(n-k)
így (4 tizedesjegyig):
ezúttal a grafikon nem szimmetrikus:
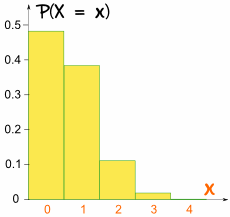
ez nem szimmetrikus!
ferde, mert P nem 0,5

Sportkerékpárok
a cég sportkerékpárokat gyárt. 90% – uk átment a végső ellenőrzésen (és 10% – uk sikertelen és rögzíteni kell).
mi a következő 4 ellenőrzés várható átlaga és szórása?
először számítsuk ki az összes valószínűséget.,
- n = 4,
- P = P(Pass) = 0,9
X a “négy ellenőrzésből származó bérletek száma”véletlen változó.
helyettesítő x = 0-4 a képletbe:
P (k az n-ből) = n!k!(n-k)! PK(1-p) (n-k)
átlag, szórás és szórás
számoljuk ki a sportkerékpár-vizsgálatok átlagát, szórását és szórását.
vannak (viszonylag) egyszerű képletek számukra. Kicsit nehéz bizonyítani, de dolgoznak!,
A jelent, vagy a “várható érték”, az, hogy:
μ = np
A képlet az Eltérés:
Variancia: σ2 = np(1-p)
, Majd a Szórás a négyzetgyök variancia:
σ = √(np(1-p))
a sport kerékpár:
Variancia: σ2 = 4 × 0.9 × 0.1 = 0.36
a Szórás:
σ = √(0.36) = 0.6


Vélemény, hozzászólás?