A Mátrix meghatározója

a mátrix meghatározója egy speciális szám, amelyet négyzetmátrixból lehet kiszámítani.

A Mátrix egy sor számok:

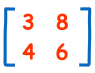
Egy Mátrix
(Ez 2 Sor 2 Oszlop)

A meghatározó, hogy a mátrix (számítások bemutatása később):

3×6 − 8×4 = 18 − 32 = -14

ez Mire jó?

a determináns segít megtalálni a mátrix inverzét, elmondja nekünk a mátrixról olyan dolgokat, amelyek hasznosak a lineáris egyenletek, kalkulusok stb.,

szimbólum

a determináns szimbóluma két függőleges vonal mindkét oldalon.

példa:

/ a/A mátrix meghatározóját jelenti a

(pontosan ugyanaz a szimbólum, mint az abszolút érték.)

A determináns kiszámítása

először a mátrixnak négyzetnek kell lennie (azaz ugyanannyi sorral kell rendelkeznie, mint az oszlopok). Akkor ez csak alapvető aritmetika., remember when you think of a cross:

Blue is positive (+ad),
Red is negative (−bc)

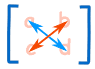
Example:

|B|= 4×8 − 6×3

= 32 − 18

= 14

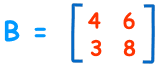
For a 3×3 Matrix

For a 3×3 matrix (3 rows and 3 columns):

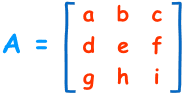
The determinant is:

|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
“The determinant of A equals .,.. etc ”

bonyolultnak tűnhet, de van egy minta:

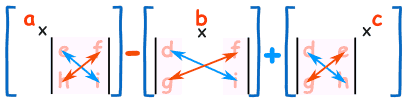
a 3×3 mátrix determinánsának kidolgozásához:

szorozza meg az A-t a 2×2 mátrix determinánsával, amely nincs a sorban vagy oszlopban.
Hasonlóképpen a b, és a c
összegezze őket, de ne feledje, a mínusz előtt a b

<| ul>

mint képlet (ne feledje, a függőleges sávok | /átlagos “determináns”):

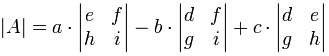
” a determináns egy alkalommal a determináns…,

= -306

A 4×4-Es Mátrix, mind Magasabb

A minta továbbra is a 4×4-es mátrix:

plusz egy alkalommal a meghatározó, a mátrix, hogy nem egy sorban vagy oszlopban,
mínusz b-szer a meghatározó, a mátrix, hogy nem a b a sorban vagy oszlopban,
plusz c-szor a meghatározója a mátrix nem ez a c-sor vagy oszlop
mínusz d szer a meghatározó, a mátrix, hogy nem a d a sorban vagy oszlopban,

Mint egy képlet: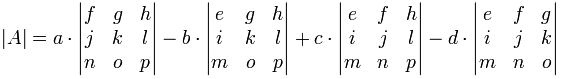

Észre a +−+− minta (+egy.,.. – b… + c… – d…). Ez fontos megjegyezni.

a minta 5×5 mátrixnál és annál magasabb. Általában a legjobb a mátrix számológép használata azok számára!

nem az egyetlen módja

Ez a számítási módszer az úgynevezett “Laplace expansion”, szeretem, mert a minta könnyen megjegyezhető. De vannak más módszerek is (csak hogy tudd).,

Összefoglalás

egy 2×2-es mátrix a determináns ad – bc

egy 3×3-as mátrix szorzás egy a meghatározó, a 2×2-es mátrix, amely nem szerepel a sorban vagy oszlopban, szintén a b, c, de ne feledjük, hogy a b-negatív jel!

a minta nagyobb mátrixoknál folytatódik: szorozzuk meg az A-t a mátrix determinánsával, amely nem az a sorban vagy oszlopban van, folytassuk így az egész sorban, de emlékezzünk a + − + − mintára.