A Pitagorasz-tétel

az egyik legismertebb matematikai képlet a Pitagorasz-tétel, amely a jobb háromszög oldalai közötti kapcsolatot biztosítja számunkra. A derékszögű háromszög két lábból és egy hipotenuszból áll. A két láb 90° – os szögben találkozik, a hypotenuse pedig a derékszögű háromszög leghosszabb oldala.,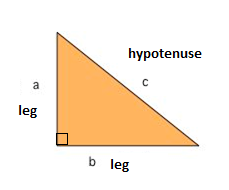

A Pitagorasz-Tétel azt mondja, hogy a kapcsolat minden igaz háromszög:

$$a^{2}+b^{2}=c^{2}$$

Példa

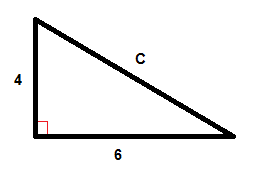
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\körülbelül 7.2$$

Van egy pár különleges típusú háromszög, mint a 45°-45° háromszög, illetve a 30°-60° – os derékszögű háromszög.,

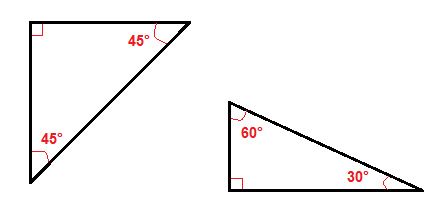
szögük miatt könnyebb megtalálni a hypotenuse-t vagy a lábakat ezekben a jobb háromszögekben, mint az összes többi jobb háromszögben.

egy 45°-45° – os derékszögű háromszögben csak az egyik lábat kell szorozni √2-vel, hogy megkapjuk a hypotenuse hosszát.

példa

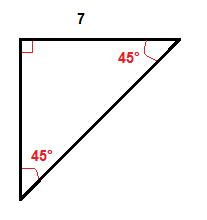
megszorozzuk a láb hosszát, amely 7 hüvelyk √2-vel, hogy megkapjuk a hypotenuse hosszát.

$ 7 \ cdot \ sqrt{2} \ Kb. 9.,9$

egy 30°-60° – os derékszögű háromszögben a 30° – os szöggel ellentétes láb hosszát a következő képlet segítségével találjuk meg:

$a = \ frac{1}{2} \ cdot c$

példa

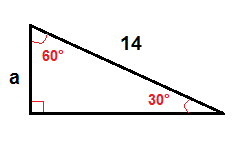
a megtalálásához a fenti képletet használjuk.

$a = \ frac{1}{2} \ cdot 14$

$a = 7$$

videó lecke

keresse meg a jobb háromszög oldalát