Bayes Statisztika kifejtette, hogy a Kezdők az Egyszerű angol

Áttekintés

• A hátránya frequentist statisztikát vezet, hogy a Bayes Statisztika
• Fedezze fel Bayes Statisztikai Következtetés Bayes
• a különböző módszerek, hogy tesztelje a jelentősége a modell, mint a p-érték, konfidencia intervallum, stb

Bevezető

Bayes Statisztika-továbbra is érthetetlen, hogy a lángra fejében a sok elemzők., A gépi tanulás hihetetlen ereje miatt sokan hűtlenné váltak a statisztikákhoz. A hangsúly a gépi tanulás felfedezésére szűkült. Nem igaz?

nem értjük, hogy a gépi tanulás nem az egyetlen módja a valós problémák megoldásának. Számos esetben ez nem segít megoldani az üzleti problémákat, annak ellenére, hogy vannak adatok ezekben a problémákban. A legkevésbé elmondható, hogy a statisztikák ismerete lehetővé teszi, hogy komplex analitikai problémákkal dolgozzon, függetlenül az adatok méretétől.,

az 1770-es években Thomas Bayes bevezette a “Bayes-tételt”. Évszázadokkal később sem szűnt meg a “Bayes-statisztika” jelentősége. Valójában ma ezt a témát nagy mélységben tanítják a világ vezető egyetemein.

ezzel az ötlettel elkészítettem ezt a kezdő útmutatót a Bayes-statisztikákról. Megpróbáltam a fogalmakat egyszerűen elmagyarázni példákkal. Az alapvető valószínűség előzetes ismerete& statisztika kívánatos., Meg kell nézd meg ezt a tanfolyamot, hogy egy átfogó alacsony statisztikai és valószínűségi.

A cikk végére, lesz egy konkrét megértése Bayes statisztika és a kapcsolódó fogalmak.,>Bayes-Tétel

Következtetés Bayes

• Bernoulli valószínűség függvény
• Előzetes Hit Engedély
• Hátsó hit Engedély

Teszt Szignifikancia – Frequentist vs Bayes

• p-érték
• Konfidencia-Intervallum
• Bayes-Faktor
• Nagy Sűrűségű Intervallum (HDI)

, Mielőtt ténylegesen ásni a Bayes Statisztika, hadd eltölteni néhány percet a megértés Frequentist Statisztikák, legnépszerűbb változat a statisztika a legtöbben találkoznak a probléma rejlik abban.,

Frequentist Statistics

a frequentist és bayesian közötti vita évszázadok óta kísérti a kezdőket. Ezért fontos megérteni a kettő közötti különbséget, és hogyan létezik egy vékony határvonal!

ez a legelterjedtebb inferenciális technika a statisztikai világban. Valójában általában ez az első gondolatiskola, hogy a statisztikai világba belépő személy találkozik.

Frequentist statisztika teszteli, hogy egy esemény (hipotézis) bekövetkezik-e vagy sem., Kiszámítja az esemény valószínűségét a kísérlet hosszú távon (azaz a kísérletet ugyanolyan körülmények között ismételjük meg az eredmény elérése érdekében).

itt rögzített méretű mintavételi eloszlásokat veszünk. Ezután a kísérletet elméletileg végtelen számú alkalommal ismételjük meg, de gyakorlatilag megállási szándékkal. Például egy kísérletet végzek egy megállási szándékkal, szem előtt tartva, hogy megállítom a kísérletet, amikor 1000-szer megismétlik, vagy legalább 300 fejet látok egy érmedobásban.

menjünk mélyebbre most.,

most, fogjuk érteni frequentist statisztikák egy példa a pénzfeldobás. A cél az érme méltányosságának becslése. Az alábbiakban egy táblázat mutatja a fejek gyakoriságát:

tudjuk, hogy a tisztességes érme dobásának valószínűsége 0,5. No. of heads a kapott fejek tényleges számát jelenti. Differencea 0.5*(No. of tosses) - no. of heads közötti különbség.,

Egy fontos megjegyezni, hogy, bár a különbség a között, hogy a tényleges szám, a fejek a várható száma fej( 50% – a száma dobálja) növeli, mint a számát dobja emelkedett, aránya száma fejek száma dobja megközelítések 0.5 (igazságos érme).

ez a kísérlet egy nagyon gyakori hibát mutat be a frekventista megközelítésben, azaz a kísérlet eredményének függése a kísérlet megismétlődésének számától.,

Ha többet szeretne tudni a frekventista statisztikai módszerekről, akkor erre a kiváló tanfolyamra léphet a következtetési statisztikákban.

A Frequentist statisztikákban rejlő hibák

eddig csak egy hibát láttunk a frequentist statisztikákban. Nos, ez csak a kezdet.

a 20.század hatalmas fellendülést mutatott a numerikus modellekre alkalmazott frekventista statisztikákban annak ellenőrzésére, hogy az egyik minta különbözik-e a másiktól, egy paraméter elég fontos ahhoz, hogy a modellben és különbözőena hipotézisvizsgálat egyéb megnyilvánulásai., De frekventista statisztikák szenvedett néhány nagy hibák a tervezés és értelmezés, amely komoly aggodalomra ad okot minden valós problémák. Például:

p-values mért minta (fix méret) statisztika néhány megállási szándék változások a változás szándék és a minta mérete. azaz ha két személy ugyanazon az adaton dolgozik, és eltérő megállási szándékuk van, akkor ugyanazon adatok esetében két különböző p- values , ami nem kívánatos.,

például: az a személy dönthet úgy, hogy abbahagyja az érme dobását, ha a teljes szám eléri a 100-at, míg a B megáll 1000-nél. A különböző mintaméretekhez különböző t-pontszámokat és különböző p-értékeket kapunk. Hasonlóképpen, a megállási szándék a rögzített számú fejtetőről a essek teljes időtartamára változhat. Ebben az esetben is kötelesek vagyunk különböző p-értékeket kapni.

2 – konfidencia intervallum (C. I) like p-value nagymértékben függ a minta méretétől., Ez teljesen abszurdvá teszi a megállási potenciált, mivel függetlenül attól, hogy hány személy végzi el a teszteket ugyanazon az adaton, az eredményeknek konzisztensnek kell lenniük.

3 – konfidencia intervallumok (C. I) nem valószínűségi eloszlások, ezért nem adják meg a legvalószínűbb értéket egy paraméterhez és a legvalószínűbb értékekhez.

Ez a három ok elég ahhoz, hogy belegondoljon a frequentista megközelítés hátrányaiba, és miért van szükség Bayes-megközelítésre. Derítsük ki.,

innen először megértjük a bayesi statisztikák alapjait.

Bayesian Statistics

” a Bayesian statistics egy matematikai eljárás, amely valószínűségeket alkalmaz a statisztikai problémákra. Ez biztosítja az embereknek az eszközöket, hogy frissítsék hitüket az új adatok bizonyítékában.”

megértetted? Hadd magyarázzam el egy példával:

tegyük fel, hogy a Niki Lauda és James hunt közötti 4 bajnoki verseny (F1) közül Niki 3-szor nyert, míg James csak 1-et.,

tehát, ha a következő verseny győztesére fogadna, ki lenne ?

fogadok, hogy Niki Laudát mondanád.

itt a csavar. Mi van, ha azt mondják, hogy egyszer esett az eső, amikor James nyert, egyszer pedig amikor Niki nyert, és biztos, hogy a következő napon esni fog. Szóval, most kire tennéd a pénzed ?

intuícióval könnyű látni, hogy James Nyerési esélyei drasztikusan növekedtek. De a kérdés az, hogy mennyi ?,

a probléma megértéséhez meg kell ismernünk néhány fogalmat, amelyek közül az első a feltételes valószínűség (az alábbiakban ismertetjük).

ezenkívül vannak bizonyos előfeltételek:

előfeltételek:

1. Lineáris Algebra: az alapok frissítéséhez megnézheti Khan Akadémia Algebráját.
2. valószínűség és Alapstatisztika: az alapismeretek frissítéséhez a Khan Academy újabb kurzusát tekintheti meg.

3.,1 Feltételes valószínűség

úgy definiáljuk, mint egy esemény valószínűsége a adott B egyenlő a valószínűsége B és a történik együtt osztva a valószínűsége B. ”

például: tegyük fel, hogy két részlegesen metsző halmazok A és B az alábbiak szerint.

az A beállítása egy eseménykészletet jelent, a B pedig egy másikat. Szeretnénk kiszámítani a valószínűsége egy adott B már megtörtént. Lehetővé teszi, hogy képviselje a történik esemény B árnyékolás azt piros.,

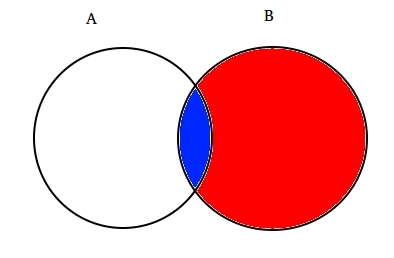
most, mivel B történt, az a rész, amely most az A számára számít, az a kék színű rész, amely érdekes módon . Tehát egy adott B valószínűsége kiderül:

ezért írhatjuk a B esemény képletét adott a már megtörtént:

vagy
/div>

most a második egyenlet átírható:

ezt feltételes valószínűségnek nevezik.,

próbáljuk megválaszolni a fogadási problémát ezzel a technikával.

tegyük fel, B az esemény a győztes James Hunt. A az esemény az eső. Ezért

az értékek helyettesítése a feltételes valószínűségi képletben 50% körüli valószínűséggel jár, ami majdnem kétszerese a 25% – nak, ha az esőt nem vették figyelembe (oldja meg a végén).

ez tovább erősítette azt a hitünket, hogy James nyer az új bizonyítékok, azaz az eső fényében., Biztos azon tűnődsz, hogy ez a képlet nagyon hasonlít valamire, amiről sokat hallottál. Gondolkozz!

valószínűleg jól kitaláltad. Úgy néz ki, mint Bayes-tétel.

a Bayes-tétel a feltételes valószínűség tetejére épül, és a Bayes-I következtetés szívében fekszik. Most értsük meg részletesen.

3.2 Bayes-tétel

Bayes-tétel akkor lép hatályba, amikor több esemény kimerítő halmazt alkot egy másik B eseménygel.,

B írható

Szóval valószínűsége, B írható,

De

Szóval, cseréje P(B) az egyenlet a feltételes valószínűség kapunk

Ez az egyenlet a Bayes-Tétel.

Bayesian Inference

nincs értelme belemerülni annak elméleti aspektusába. Tehát megtanuljuk, hogyan működik!, Vegyünk egy példát az érme dobására, hogy megértsük a Bayes-I következtetés mögött rejlő ötletet.

a bayesi következtetés fontos része a paraméterek és modellek kialakítása.

a modellek a megfigyelt események matematikai formulái. A paraméterek a megfigyelt adatokat befolyásoló modellek tényezői. Például egy érme feldobásakor az érme méltányossága meghatározható a θ által jelölt érme paramétereként. Az események kimenetelét D.

válaszolj erre most., Mekkora a valószínűsége annak, hogy 9-ből 4 fej dob(D), figyelembe véve az érme méltányosságát (θ). i. e P(D|θ)

várj, feltettem a helyes kérdést? Nem.

kellene tudni, hogy : Adott egy eredmény (D) mi a probbaility érme fair (θ=0.5)

Lehetővé teszi, hogy képviselje a Bayes-Tétel:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

Itt P(θ) az előzetes én.az e az erő, a hit, a tisztesség, az érme, mielőtt a dobás., Ez teljesen rendben van, hogy úgy vélik, hogy érme lehet bármilyen fokú méltányosság között 0 és 1.

P(D|θ) valószínű, hogy megfigyeljük eredményünket a θ eloszlása miatt. Ha tudtuk, hogy az érme tisztességes, ez megadja annak valószínűségét, hogy megfigyeljük a fejek számát egy adott számú fejben.

P(D) a bizonyíték. Ez az adat valószínűsége, amelyet a θ összes lehetséges értékének összegzése (vagy integrálása) határoz meg, súlyozva azzal, hogy mennyire hiszünk a θ ezen értékeiben.,

Ha több nézet, hogy mi a tisztesség, az érme (de nem biztos), akkor ez azt mondja, a valószínűsége annak, hogy látva egy bizonyos sorrend a fejtetőre, minden lehetőséget a hit az érme méltányosság.

P(θ|D) paramétereink hátsó hite a bizonyítékok megfigyelése után, azaz a fejek száma.

innen mélyebben belemerülünk ennek a koncepciónak a matematikai következményeibe. Ne aggódj. Miután megértette őket, a matematikához való hozzáférés nagyon egyszerű.,

a modell helyes meghatározásához két matematikai modellre van szükségünk kéz előtt. Az egyik a p(d|θ) valószínűségi függvényt képviseli ,a másik pedig a korábbi hiedelmek eloszlását. E kettő terméke adja a posterior hit p (θ|D) eloszlását.

mivel a prior és a posterior egyaránt hiedelmek az érme igazságosságának eloszlásáról, az intuíció azt mondja nekünk, hogy mindkettőnek azonos matematikai formával kell rendelkeznie. Ezt tartsd észben. Vissza fogunk térni hozzá.,

tehát számos olyan függvény létezik, amelyek támogatják a bayes-tétel létezését. Fontos tudni őket, ezért részletesen elmagyaráztam őket.

4.1. Bernoulli valószínűségi függvény

lehetővé teszi, hogy összefoglalja, mit tanultunk a valószínűségi függvény. Tehát megtudtuk, hogy:

ez annak a valószínűsége, hogy egy adott számú fejet megfigyelnek egy adott számú fejben egy adott érme méltányosságáért. Ez azt jelenti, hogy a fej/farok megfigyelésének valószínűsége az érme (θ) tisztességességétől függ.,

P(y=1|θ)=

P(y=0|θ)=

érdemes megjegyezni, hogy az 1 fejként és 0 farkként való ábrázolása csak matematikai jelölés egy modell megfogalmazására. A fenti matematikai definíciókat egyetlen definícióval kombinálhatjuk, hogy mindkét eredmény valószínűségét reprezentáljuk.

P(y|θ)=

ezt Bernoulli valószínűségi függvénynek nevezik, és az érmefeldobás feladatát Bernoulli kísérleteinek nevezik.,

és ha fej-vagy fejsorozatot akarunk látni, annak valószínűségét a következő adja meg:

továbbá, ha érdekel a valószínűsége, hogy a fejek száma z felbukkanó n számú fejek, akkor a valószínűség által megadott:

4.2. Előzetes Hitelosztás

ez az eloszlás a korábbi tapasztalatok alapján a paraméterekkel kapcsolatos hiedelmekre vonatkozó erősségeink reprezentálására szolgál.,

de mi van, ha nincs korábbi tapasztalata?

ne aggódjon. A matematikusok módszereket dolgoztak ki a probléma enyhítésére is. uninformative priorsnéven ismert. Szeretném előzetesen tájékoztatni Önt arról, hogy ez csak egy helytelen elnevezés. Minden uninformative prior mindig ad néhány információt esemény az állandó forgalmazás előtt.

Nos, a korábbi hiedelmek ábrázolására használt matematikai függvény., Nagyon szép matematikai tulajdonságokkal rendelkezik, amelyek lehetővé teszik számunkra, hogy modellezzük a binomiális eloszlással kapcsolatos hiedelmeinket.

A béta-Eloszlás valószínűségi sűrűségfüggvénye a következő:

ahol a hangsúly a számlálón marad. A nevező csak azért van, hogy biztosítsa, hogy az integráláskor a teljes valószínűségi sűrűség függvény 1-re értékeljen.

α és β a sűrűségfüggvény alakmeghatározó paramétereinek nevezzük., Ittα megegyezik a próbákban részt vevő fejek számával, és β megfelel a farok számának., Az alábbi ábrák segítenek a béta-eloszlások megjelenítésében a α és β

a béta-eloszlást az R:

megjegyzés: α és β intuitív megérteni, mivel ezek kiszámíthatók az eloszlás középértékének (μ) és szórásának (σ) ismeretében., Valójában ezek a következők:

Ha egy Eloszlás átlagos és standard eltérése ismert , akkor az alakparaméterek könnyen kiszámíthatók.

a fenti grafikonokból levonható következtetés:

1. amikor nem volt dobás, úgy gondoltuk, hogy az érme minden méltányossága lehetséges, amint azt a lapos vonal ábrázolja.
2. amikor több fej volt, mint a farok, a grafikon a jobb oldal felé eltolt csúcsot mutatott, jelezve a fejek nagyobb valószínűségét, és az érme nem tisztességes.,
3. mivel több dobás történik, a fejek továbbra is nagyobb arányban jönnek, a csúcs szűkíti az érme értékének igazságosságába vetett bizalmunkat.

4.3. Posterior hit Distribution

az ok, hogy úgy döntöttünk, előzetes hit, hogy szerezzen egy béta-Eloszlás. Ez azért van, mert ha megszorzunk a valószínűsége funkció, posterior eloszlás hozamok egy formája hasonló az előzetes engedély ami sokkal könnyebb azonosulni megérteni., Ha ez a sok információ felkeltette az étvágyát, biztos vagyok benne, hogy készen áll egy további mérföldre.

számítsuk ki a hátsó hitet a bayes-tétel segítségével.

kiszámítása posterior hit segítségével Bayes tétel

most, a hátsó hit válik,

div id=”243f3b5b18″>

ez érdekes., Csak a θ paraméterrel kapcsolatos hitünk átlagos és standard eloszlásának ismeretében, valamint a fejek számának N-ben történő megfigyelésével frissíthetjük a modellparaméterre vonatkozó hitünket (θ).

lehetővé teszi, hogy megértsük ezt egy egyszerű példa segítségével:

tegyük fel, hogy úgy gondolja, hogy egy érme elfogult. Az átlagos (μ) torzítás 0, 6 körül van, a szórás 0, 1.

ezután

α= 13.8 , β=9.2

i.,e terjesztésünk a jobb oldalon elfogult lesz. Tegyük fel, hogy 80 fejet (z=80) megfigyelt 100 fejben(N=100). Lássuk, hogy az előzetes, a hátsó, a hit fog kinézni:

prior = P(θ|α,β)=P(θ|13.8,9.2) Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

Lehetővé teszi, hogy szemléltesse, mind a hiedelmek egy grafikon:

A R kódot a fenti grafikon, mint:

}

Ahogy egyre több fejtetőre készülnek, de az új adatok figyelhető meg, hitünk frissülnek., Ez a Bayes-I következtetés valódi ereje.

szignifikancia – Frekventista vs Bayesian

a szigorú matematikai struktúrákba való belépés nélkül ez a szakasz gyors áttekintést nyújt a frequentist és bayesian módszerek különböző megközelítéseiről, hogy teszteljék a csoportok közötti jelentőséget és különbséget, és melyik módszer a legmegbízhatóbb.

5.1. p-érték

ebben kiszámítjuk egy adott minta t-pontszámát egy rögzített méretű mintavételi eloszlásból. Ezután a p-értékeket előre jelezzük., Tudjuk értelmezni p-értékek, mint (egy példa a p-érték, mint 0.02 egy megoszlása 100) : van 2% a valószínűsége, hogy a minta lesz jelenti, egyenlő 100.

ez az értelmezés abban a hibában szenved, hogy a különböző méretű mintavételi eloszlások esetében az egyiknek eltérő t-pontszámot kell kapnia, tehát eltérő p-értéket. Ez teljesen abszurd. Az 5% – nál kisebb p-érték nem garantálja, hogy a null hipotézis helytelen, sem az 5% – nál nagyobb p-érték biztosítja, hogy a null hipotézis helyes.

5.2., A konfidencia intervallumok

a konfidencia intervallumok szintén ugyanazt a hibát szenvedik. Ráadásul mivel a C. I nem valószínűségi eloszlás, nem lehet tudni, hogy mely értékek a legvalószínűbbek.

5.3. Bayes Factor

Bayes factor is the equivalent of P-value in the bayesian framework. Lehetővé teszi, hogy megértsük, hogy egy átfogó módon.

a bayesi keretrendszerben a null-hipotézis csak egy paraméter (mondjuk θ=0.5) meghatározott értékén feltételezi a ∞ valószínűségi eloszlást, és egy nulla valószínűséget, ahol., (M1)

az alternatív hipotézis az, hogy a θ összes értéke lehetséges, tehát az eloszlást ábrázoló lapos görbe. (M2)

most az új adatok hátsó eloszlása az alábbiak szerint néz ki.

Bayesiai statisztikák korrigált hitelességét (valószínűség) a különböző értékek θ. Könnyen látható, hogy a valószínűségi eloszlás az M2 felé tolódott el, amelynek értéke magasabb, mint az M1, azaz az M2 nagyobb valószínűséggel fordul elő.,

Bayes faktor nem függ a θ tényleges eloszlási értékeitől, hanem az M1 és M2 értékek eltolódásának nagyságától.

az a panelen( fent látható): a bal oldali sáv (M1) A null hipotézis előzetes valószínűsége.

A B panelen (látható) a bal sáv A null hipotézis hátsó valószínűsége.

Bayes faktor meghatározása szerint az arány a hátsó esélye, hogy a korábbi esélyek,

elutasítása null hipotézis, a BF < 1/10 előnyös.,

láthatjuk a Bayes faktor használatának közvetlen előnyeit a p-értékek helyett, mivel függetlenek a szándékoktól és a minta méretétől.

5.4. Nagy sűrűségű intervallum (HDI)

a HDI az új adatok megfigyelése után a hátsó eloszlásból alakul ki. Mivel a HDI valószínűség, a 95% HDI adja a 95% leghitelesebb értékeket. Az is garantált, hogy a 95% – os értékek ebben az intervallumban fekszenek, ellentétben a C. I.

értesítéssel, hogy a 95% – os HDI előzetes eloszlásban szélesebb, mint a 95% – os hátsó Eloszlás., Ennek oka az, hogy a HDI-be vetett hitünk növekszik az új adatok megfigyelésekor.

végjegyzetek

ennek a cikknek az volt a célja, hogy elgondolkodjon az ottani statisztikai filozófiák különböző típusain, és hogy egyik sem használható minden helyzetben.

itt az ideje, hogy mindkét filozófia összeolvadjon, hogy enyhítse a valós világ problémáit a másik hibáinak kezelésével., A sorozat II. része az MCMC (Markov Chain Monte Carlo) algoritmusokat használó Méretcsökkentési technikákra összpontosít. A III. rész alapja egy Bayes regressziós modell létrehozása a semmiből, majd annak eredményeinek értelmezése R. tehát, mielőtt elkezdeném a II. részt, szeretném megkapni javaslatait / visszajelzéseit erről a cikkről.