nyomás és KMT
a nyomás makroszkopikus jelenségei a gázok kinetikus molekuláris elméletével magyarázhatók. Tegyük fel azt az esetet, amikor egy gázmolekula (amelyet egy gömb képvisel) egy l hosszúságú dobozban van (1.ábra). A fenti feltevések felhasználásával, és figyelembe véve, hogy a gömb csak x irányban mozog, megvizsgálhatjuk a gömbnek a doboz egyik falával rugalmasan ütköző példányát.,
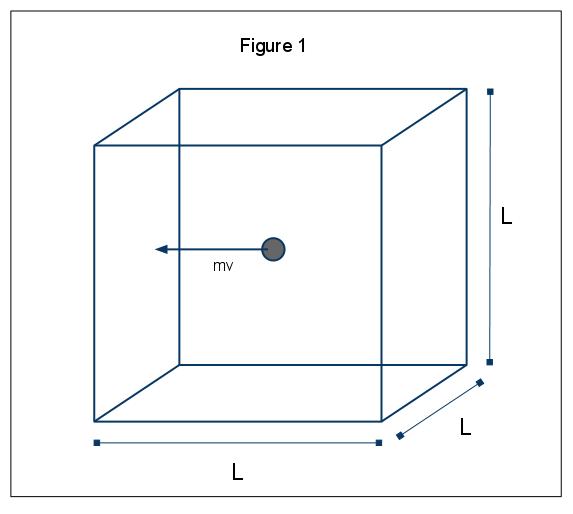
az ütközés lendületét p=mv adja, ebben az esetben p=mvx, mivel csak az x dimenziót vesszük figyelembe. Az ütközés teljes lendületváltozását ezután a
\
adja meg, tekintettel arra, hogy a molekula falával való ütközése közötti idő l/vx, a molekula ütközésének gyakoriságát a doboz egy adott falához egy egységnyi idő alatt vx / 2L-ként adhatjuk meg., Most már megoldható a lendület időegységenkénti változása:
\
az időegységenkénti lendület megoldása az objektum által kifejtett erőt adja (F = ma = p / idő)., Az a kifejezés, hogy F=mvx2/L lehet már oldani a nyomást fejt ki a molekuláris ütközés, ahol a terület adott, mint a terület egyik falon a doboz, A=L2:
\
\
A kifejezés most írt feltételeket a nyomás kapcsolódó ütődéseket N számú molekulák:
\
Ez a kifejezés most lehet beállítani, hogy figyelembe a mozgás az x, y, z irányban segítségével értem-tér-sebesség három dimenzióban nagy értéke N., A kifejezés most a következőképpen íródott:
\
Ez a kifejezés most nyomást, makroszkopikus minőséget ad az atommozgás szempontjából. A fenti kapcsolat jelentősége az, hogy a nyomás arányos az adott tartályban lévő molekulák átlagos négyzetsebességével. Ezért a molekuláris sebesség növekedésével a tartályra gyakorolt nyomás is növekszik.
Vélemény, hozzászólás?