háromfázisú Wye(Y) Kapcsolat
Kezdetben, fedezzük fel az ötlet, hogy három-fázisú rendszerek összekapcsolásával három feszültség források együtt közismert nevén az “Y” (vagy a “csillag”) konfiguráció.
a feszültségforrások ezen konfigurációját az egyes források egyik oldalához csatlakozó közös csatlakozási pont jellemzi., (Az alábbi ábra)
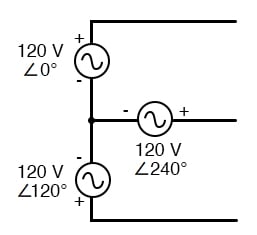
háromfázisú “Y” kapcsolat három feszültségforrással van összekötve egy közös ponthoz.
ha rajzolunk egy áramkört, amely minden feszültségforrást huzal tekercsnek (generátor vagy transzformátor tekercselés) mutat, és némi átrendezést végez, az “Y” konfiguráció az alábbi ábrán nyilvánvalóbbá válik.

háromfázisú, négyvezetékes” Y “kapcsolat” közös ” negyedik vezetéket használ.,
a feszültségforrásoktól (tekercsektől) a terhelés felé vezető három vezetőt általában vonalaknak nevezik, míg magukat a tekercseket általában fázisoknak nevezik.
egy Y-csatlakoztatott rendszerben lehet, hogy (az alábbi ábra) semleges vezeték van a középső csomóponton, bár ez minden bizonnyal segít enyhíteni a lehetséges problémákat, ha a háromfázisú terhelés egyik eleme nem nyílik meg, amint azt korábban tárgyaltuk.
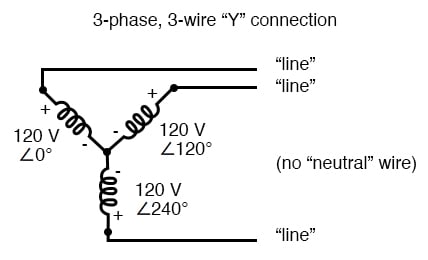
háromfázisú, háromvezetékes” Y ” kapcsolat nem használja a semleges vezetéket.,
feszültség és Áramértékek háromfázisú rendszerekben
amikor háromfázisú rendszerekben mérjük a feszültséget és az áramot, pontosan meg kell határoznunk, hogy hol mérjük.
A vonalfeszültség a kiegyensúlyozott háromfázisú rendszer bármely két vonalvezetője között mért feszültség mennyiségére vonatkozik. A fenti áramkörrel a vonal feszültsége nagyjából 208 volt.
A fázisfeszültség bármely komponens (forrás tekercselés vagy terhelési impedancia) között mért feszültségre vonatkozik kiegyensúlyozott háromfázisú forrás vagy terhelés esetén.
a fent bemutatott áramkör esetében a fázisfeszültség 120 volt., Az aktuális és fázisáram kifejezések ugyanazt a logikát követik: az előbbi az áramra utal bármely vonalvezetőn keresztül, az utóbbi pedig az áramra bármely komponensen keresztül.
Y-csatlakoztatott források és terhelések mindig a fázisfeszültségeknél nagyobb feszültségekkel rendelkeznek, és a vonaláramok megegyeznek a fázisáramokkal., Ha az Y-csatlakoztatott forrás vagy terhelés kiegyensúlyozott, akkor a vonal feszültsége megegyezik a 3:

négyzetgyökével, azonban az “Y” konfiguráció nem az egyetlen érvényes a háromfázisú feszültségforrás vagy terhelési elemek összekapcsolására.
háromfázisú Delta(Δ) konfiguráció
egy másik konfiguráció “Delta” néven ismert, mivel geometriai hasonlóságot mutat az azonos nevű görög betűvel (Δ). Vegye figyelembe az alábbi ábrán szereplő egyes tekercsek polaritását.,
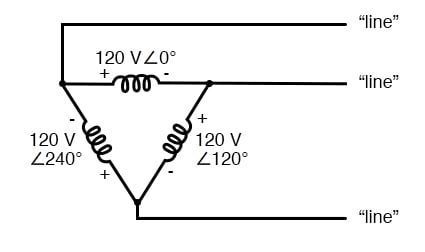
háromfázisú, háromvezetékes Δ kapcsolat nincs közös.
első pillantásra úgy tűnik, mintha három ilyen feszültségforrás rövidzárlatot hozna létre, az elektronok a háromszög körül áramlanak, csak a tekercsek belső impedanciájával, hogy visszatartsák őket.
e három feszültségforrás fázisszögei miatt azonban nem ez a helyzet.,
Kirchhoff Feszültségtörvénye Delta csatlakozásokban
ennek egy gyors ellenőrzése Kirchhoff Feszültségtörvényének használata annak megállapítására, hogy a hurok körül lévő három feszültség nulla-e. Ha igen, akkor nem lesz feszültség, amely az áramot a hurok körül és körül mozgatná, következésképpen nem lesz keringő áram.
a felső tekercseléssel és az óramutató járásával ellentétes irányban haladva a KVL kifejezésünk valahogy így néz ki:

valóban, ha ezt a három vektormennyiséget együtt adjuk hozzá, akkor nullára nőnek., Egy másik módja, hogy ellenőrizze a tény, hogy ez a három feszültség forrásai lehetnek egymáshoz a hurok nélkül, ami a keringő áram, hogy nyissa fel a hurok egy junction point, majd kiszámítja a feszültség át a szünet: (az alábbi ábrát)

A feszültség át nyitva Δ nullának kell lennie.,
A jobb oldali tekercseléssel (120 V ∠ 120°) kezdve és az óramutató járásával ellentétes irányban haladva KVL-egyenletünk így néz ki:

biztos, hogy a szünetben nulla feszültség lesz, mondván, hogy egyetlen áram sem kering a tekercsek háromszög alakú hurkán belül, amikor a kapcsolat befejeződött.
miután megállapítottuk, hogy egy Δ-csatlakoztatott háromfázisú feszültségforrás a keringő áramok miatt nem éget ropogósra, a háromfázisú áramkörök áramforrásaként való gyakorlati felhasználásához fordulunk.,
mivel minden vonalvezetőpár közvetlenül egy Δ áramkör egyetlen tekercsén keresztül van csatlakoztatva, a vonal feszültsége megegyezik a fázisfeszültséggel.
fordítva, mivel minden vonalvezető két tekercs közötti csomóponthoz kapcsolódik, a vonaláram a két összekötő fázisáram vektorösszege lesz.,
nem meglepő, hogy a Δ konfiguráció kapott egyenletei a következők:

Delta Connection Example Circuit Analysis
lássuk, hogyan működik ez egy példaáramkörben: (az alábbi ábra)

A δ forrás terhelése δ-ban van vezetve.
Ha minden terhelési ellenállás 120 V-ot kap a forrás megfelelő fázistekercsétől, az áramkör minden fázisában az áram 83 lesz.,33 amper:

A Delta háromfázisú rendszer előnyei
tehát ebben a háromfázisú villamosenergia-rendszerben minden egyes vonaláram 144,34 amper, ami lényegesen több, mint az Y-csatlakoztatott rendszer vonaláramai, amelyeket korábban megvizsgáltunk.
lehet, hogy csoda, ha már elvesztette minden előnyét háromfázisú teljesítmény itt, tekintettel arra, hogy van ilyen nagyobb vezeték áramok, szükségessé vastagabb, drágább vezetéket.
a válasz nem., Bár ez az áramkör három 1-es számú rézvezetéket igényelne (1000 láb távolságra a forrás és a terhelés között ez valamivel több mint 750 font réznek felel meg az egész rendszer számára), még mindig kevesebb, mint az egyfázisú rendszerhez szükséges 1000+ font réz, amely ugyanazt a teljesítményt (30 kW) biztosítja ugyanabban a feszültségben (120 voltos vezető-vezető).
A Δ-csatlakoztatott rendszer egyik külön előnye a semleges vezeték hiánya., Y csatlakozó rendszer, egy semleges drót volt szükség abban az esetben, ha a fázis-terhelés nem sikerül megnyitni (vagy ki van kapcsolva), annak érdekében, hogy a fázis feszültség a terhelés a változó.
Ez nem szükséges (vagy akár lehetséges!) Δ-kapcsolt áramkörben.
minden egyes terhelési fáziselemnél, amely közvetlenül kapcsolódik egy adott forrásfázis-tekercshez, a fázisfeszültség állandó lesz, függetlenül a terhelési elemek nyílt hibáitól.
talán a Δ-csatlakoztatott forrás legnagyobb előnye a hibatűrés.,
lehetséges, hogy a Δ-csatlakoztatott háromfázisú forrás egyik tekercse nem nyílik meg (az alábbi ábra) anélkül, hogy befolyásolná a terhelési feszültséget vagy az áramot!

még forrás tekercselési hiba esetén is a vonal feszültsége még mindig 120 V, A terhelési fázis feszültsége pedig még mindig 120 V. az egyetlen különbség az extra áram a fennmaradó funkcionális forrás tekercsekben.
Az egyetlen következménye a forrás tekercselés hiányában nyitott Δ-csatlakoztatott forrás fokozott fázisáram a fennmaradó tekercsek., Hasonlítsa össze ezt a hibatűrést egy Y-csatlakozású rendszerrel, amely az alábbi ábrán nyílt forráskódú tekercset szenved.

nyissa meg az” Y ” forrástekercselő felezi a feszültséget a Δ két terhelésnél, összekötve a terhelést.
Δ-csatlakoztatott terheléssel az ellenállások közül kettő csökkentett feszültséget szenved, míg az egyik az eredeti vonalfeszültségen marad, 208. Az Y-csatlakozású terhelés még rosszabb sorsot szenved (az alábbi ábra), ugyanazzal a tekercselési hibával egy Y-csatlakozású forrásban.,

az” Y-Y ” rendszer nyílt forráskódú tekercselése felezi a feszültséget két terhelésnél, és egy terhelést teljesen elveszít.
ebben az esetben két terhelésellenállás csökkentett feszültséget szenved, míg a harmadik teljesen elveszíti a tápfeszültséget! Ezért a Δ-csatlakoztatott források előnyben részesülnek a megbízhatóság szempontjából.
Ha azonban kettős feszültségre van szükség (például 120/208), vagy az alacsonyabb Vonalú áramoknál előnyben részesítik, az Y-csatlakoztatott rendszerek a választás konfigurációja.,
áttekintés:
- a háromfázisú forrás vagy terhelés három pontjához csatlakoztatott vezetékeket soroknak nevezzük.
- a háromfázisú forrást vagy terhelést tartalmazó három komponenst fázisoknak nevezzük.
- a vonalfeszültség a háromfázisú áramkör bármely két vonala között mért feszültség.
- a fázisfeszültség az egyetlen komponensben mért feszültség háromfázisú forrás vagy terhelés esetén.
- a Vonaláram a háromfázisú forrás és a terhelés közötti bármely vonalon átáramló áram.,
- a fázisáram az áram bármely olyan komponensen keresztül, amely háromfázisú forrást vagy terhelést tartalmaz.
- kiegyensúlyozott “Y” áramkörökben a vonal feszültsége megegyezik a 3 négyzetgyökének fázisfeszültségével, míg a vonaláram egyenlő a fázisárammal.

- A kiegyensúlyozott Δ áramkörök, a hálózati feszültség megegyezik a fázis feszültség, míg a vonal jelenlegi egyenlő fázis aktuális alkalommal a négyzetgyöke 3.

Vélemény, hozzászólás?