ebben a leckében, fogunk építeni az öt (5) közös logikai melléknevek VAGY operátorok. Közös logikai konnektíveknek tekintik őket, mert nagyon népszerűek, hasznosak és mindig együtt tanítják őket.
mielőtt elkezdenénk, azt javaslom, hogy vizsgálja felül a másik leckét, amelyben a link az alábbiakban látható.
Ez a bevezető lecke az igazságtáblákról olyan előfeltétel-ismereteket vagy információkat tartalmaz, amelyek segítenek jobban megérteni ennek a leckének a tartalmát.,
Bevezetés Az igazság táblázatokba, Kijelentésekbe és Melléknevekbe
Le kezdete az öt (5) közös logikai melléknév felsorolásával.
The Five (5) Common Logical Connectives or operátorok
- logikai Negation
- logikai összefüggés (AND)
- logikai implikáció (feltételes)
- logikai kétkomponensű (kettős implikáció)
logikai diszjunkció (Inclusive OR)
I., A logikai negáció igazságtáblája
a kijelentés tagadása olyan állítás is, amelynek igazságértéke pontosan ellentétes az eredeti állítással. Például, a tagadás a nyilatkozat van írva szimbolikusan
~\large{p} vagy \large{\neg p}.
~{p} vagy {\neg p}”nem P.”
ne feledje: A ~ vagy \neg szimbólummal jelölt negációs operátor az eredeti állítás igazságértékét veszi át, majd az igazságértékének pontos ellentétét adja ki., Más szavakkal, a tagadás egyszerűen megfordítja egy adott kijelentés igazságértékét. Így, ha a P állítás igaz, akkor a negáció igazságértéke hamis. Ugyanígy, ha p hamis, akkor a negáció igazságértéke igaz.

II. Igazság Táblázat a Logikai Összefüggésben
együttesen egy olyan típusú vegyület nyilatkozata, hogy áll a két javaslatok (úgy is ismert, mint egyszerű mondatok) csatlakozott a tartó.,
a \color{red}\Large{\wedge} függvényt ábrázoló szimbólum. Úgy néz ki, mint egy fordított betű V.
ha van két egyszerű kijelentés P és Q, és azt szeretnénk, hogy egy összetett nyilatkozatot csatlakozott az és az Üzemeltető, tudjuk írni, mint:
\large{p \wedge Q}.
{p \wedge Q}”P és q”
ne feledje: a P \wedge Q összetett állítás igazságértéke csak akkor igaz, ha a P és a Q igaz értékek egyaránt igazak., Ellenkező esetben a P \wedge Q hamis.
figyeljük meg az alábbi igazságtáblázatban, hogy ha p igaz és Q igaz, akkor P \wedge Q igaz. A P és Q javaslatok másik három kombinációja azonban hamis.

III. Truth Table of Logical Disjunction
a disjunction egyfajta összetett kijelentés, amely két egyszerű kijelentésből áll, amelyeket a logikai Disjunction
az or operátor.
egy diszjunkciós nyilatkozatban az OR használata inclusive. Ez azt jelenti, hogy “az egyik vagy a másik” vagy mindkettő.,
A vagy logikai diszjunkciós operátor ábrázolására használt szimbólum \color{red} \ Large{ \vee }. Ez hasonlít az ábécé V betűjére.
két javaslat P és Q egyesítve vagy operátor alkotnak egy összetett nyilatkozat van írva:
\ large{p \vee Q}.
{p \vee Q}”P vagy q”
ne feledje: a P \vee Q összetett állítás igazságértéke akkor igaz, ha a két egyszerű P és Q állítás igazsága igaz., Moreso, P \vee Q akkor is igaz, ha mind a P, mind a Q állítások igazságértékei igazak. Azonban az egyetlen alkalom, amikor a P \Vee Q diszjunkciós kijelentés hamis, akkor történik, amikor mind a P, mind a Q igazságértékei hamisak.
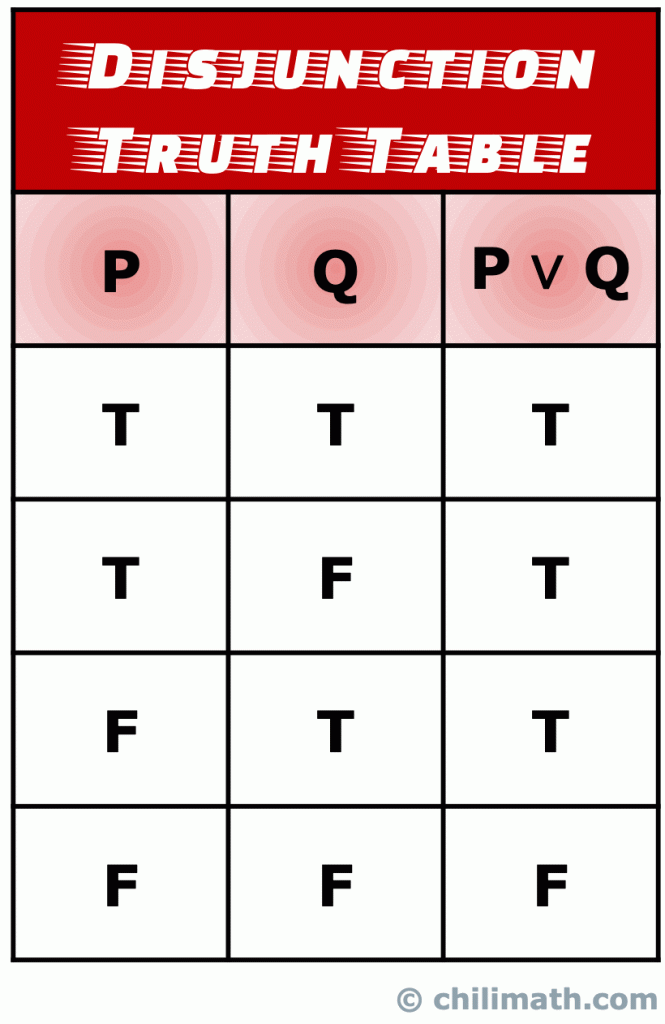
IV kijelentések a logikai implikáció kötőszó vagy operátor. ,
a logikai implikáció operátor ábrázolására használt szimbólum egy jobbra mutató nyíl, tehát egy jobbra mutató nyíl.

Amikor két egyszerű mondatok P Q csatlakozott a következménye, operátor van:
\Nagyméretű{P \Q}.
- ahol P az úgynevezett hipotézis
- ahol Q ismert, mint a következtetés
számos módja van, hogyan kell olvasni a feltételes {P \to Q}., Az alábbiakban néhány a néhány közös is.
ne feledje: a P \to Q összetett kijelentés igazságértéke akkor igaz, ha mind a P, mind a Q egyszerű kijelentések igazak. Moreso, P \to Q mindig igaz, ha p hamis. Az egyetlen forgatókönyv, hogy P \to Q hamis történik, ha p igaz, Q pedig hamis.
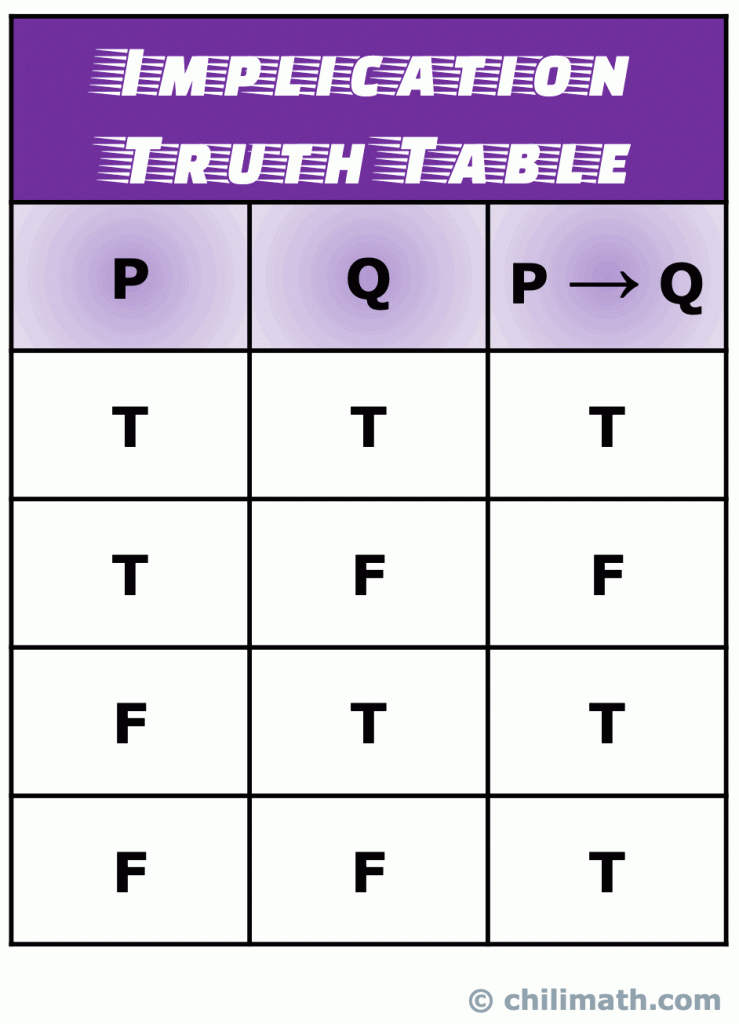
V., Truth Table of Logical Biconditional or Double Implication
a double implication (más néven kétkomponensű kijelentés) egy olyan típusú összetett kijelentés, amely úgy alakul ki, hogy két egyszerű kijelentést csatlakoztat a kétkomponensű operátorhoz. A kétkomponensű kijelentés valójában egy feltételes kijelentés és annak konverse kombinációja.
a kétkomponensű operátort kétfejű nyíl jelöli.,

Ha csatlakozik két egyszerű mondatok (úgy is ismert, mint a molekuláris nyilatkozatok) a biconditional üzemeltető kapunk:
\Nagyméretű{P \leftrightarrow Q}
{P \leftrightarrow Q} olvasni, mint a “P ha pedig csak akkor, ha K.,”
- ahol P az előzményként ismert
- ahol Q A következményként ismert
ne feledje: a bicontional állítás igazságértéke P \leftrightarrow Q igaz, ha mind a P, mind a Q egyszerű kijelentések igazak vagy mindkettő hamis. Ellenkező esetben a P \ leftrightarrow Q hamis.
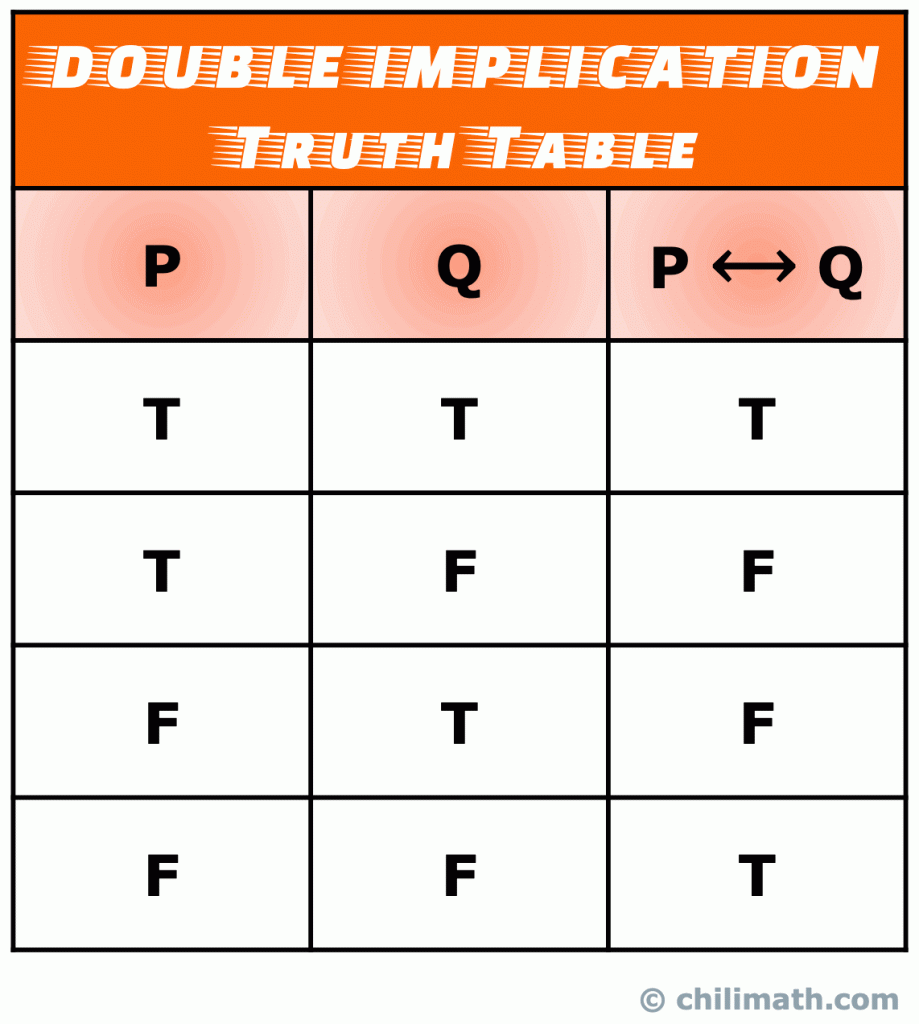
érdekelhetik a következők is:
Bevezetés Az Igazságtáblákba, Kijelentésekbe és logikai Konnektorokba
feltételes kijelentés kontrapozitív
Vélemény, hozzászólás?