Il determinante di una matrice è un numero speciale che può essere calcolato da una matrice quadrata.
Una Matrice è una matrice di numeri:
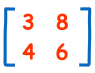
Matrix
(Questo ha 2 Righe e 2 Colonne)
Il determinante di tale matrice (i calcoli sono spiegati più avanti):
che Cosa serve?
Il determinante ci aiuta a trovare l’inverso di una matrice, ci dice cose sulla matrice che sono utili nei sistemi di equazioni lineari, calcolo e altro ancora.,
Simbolo
Il simbolo per il determinante è due linee verticali su entrambi i lati.
Esempio:<|p>
| A/indica il determinante della matrice A
(Esattamente lo stesso simbolo del valore assoluto.)
Calcolando il Determinante
Prima di tutto la matrice deve essere quadrata (cioè avere lo stesso numero di righe delle colonne). Quindi è solo aritmetica di base., remember when you think of a cross:
- Blue is positive (+ad),
- Red is negative (−bc)
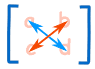
Example:
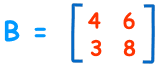
For a 3×3 Matrix
For a 3×3 matrix (3 rows and 3 columns):
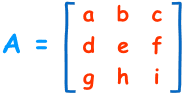
The determinant is:
|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
“The determinant of A equals .,.. etc ”
Può sembrare complicato, ma c’è un modello:
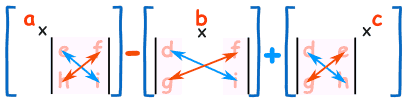
Per calcolare il determinante di una matrice 3×3:
- Moltiplica a per il determinante della matrice 2×2 che non è nella riga o nella colonna di a.
- Allo stesso modo per b, e per c
- Sommali, ma ricorda il meno davanti al b
Come formula (ricorda le barre verticali || significano “determinante di”):
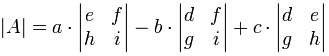
“Il determinante di A è uguale a per il determinante di …,
Per 4×4 Matrici e Superiore
Il modello continua per 4×4 matrici:
- più volte il determinante della matrice che non è in una riga o colonna,
- minus b volte il determinante della matrice che non è in b di riga o di colonna,
- plus c volte il determinante della matrice che non è in c di riga o di colonna,
- meno d volte il determinante della matrice che non è in d di riga o di colonna,

Come una formula:
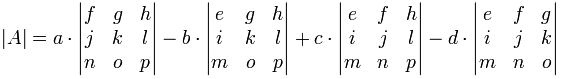
si Noti il +−+− pattern (+di una.,.. −B… +C… – d…). Questo è importante da ricordare.
Il modello continua per matrici 5×5 e superiori. Di solito meglio usare una calcolatrice matrice per quelli!
Non è l’unico modo
Questo metodo di calcolo è chiamato “espansione di Laplace” e mi piace perché il modello è facile da ricordare. Ma ci sono altri metodi (solo così lo sai).,
Sommario
- Per una matrice 2×2 il determinante è ad – bc
- Per una matrice 3×3 moltiplicare a per il determinante della matrice 2×2 che non è nella riga o colonna di a, allo stesso modo per b e c, ma ricorda che b ha un segno negativo!
- Il pattern continua per matrici più grandi: moltiplica a per il determinante della matrice che non si trova nella riga o nella colonna di a, continua così per tutta la riga, ma ricorda il + − + − pattern.
Lascia un commento