Il Teorema di Pitagora

Una delle formule matematiche più conosciute è il Teorema di Pitagora, che ci fornisce la relazione tra i lati in un triangolo rettangolo. Un triangolo rettangolo consiste di due gambe e un’ipotenusa. Le due gambe si incontrano con un angolo di 90° e l’ipotenusa è il lato più lungo del triangolo rettangolo ed è il lato opposto all’angolo retto.,

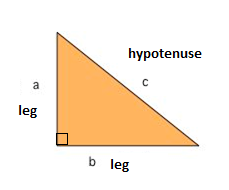
Il Teorema di Pitagora ci dice che il rapporto in ogni triangolo rettangolo è:

$$a^{2}+b^{2}=c^{2}$$

Esempio

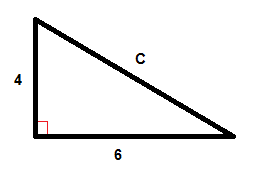
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\ca 7.2$$

Ci sono un paio di particolari tipi di triangoli, come il 45°-45° triangoli e i 30°-60° triangolo a destra.,

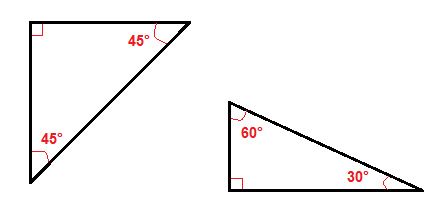
A causa dei loro angoli è più facile trovare l’ipotenusa o le gambe in questi triangoli rettangoli che in tutti gli altri triangoli rettangoli.

In un triangolo rettangolo di 45°-45° dobbiamo solo moltiplicare una gamba per √2 per ottenere la lunghezza dell’ipotenusa.

Esempio

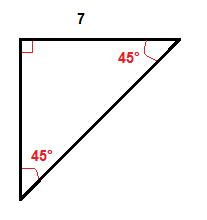
Moltiplichiamo la lunghezza della gamba che è di 7 pollici per √2 per ottenere la lunghezza dell’ipotenusa.

$ $ 7\cdot \sqrt{2}\circa 9.,9 In

In un triangolo rettangolo di 30°-60° possiamo trovare la lunghezza della gamba opposta all’angolo di 30° usando questa formula:

a a=\frac{1}{2}\cdot c Example

Esempio

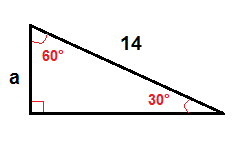
Per trovare a, usiamo la formula sopra.

$ $ a=\frac{1}{2}\cdot 14<

a a=7 lesson

Video lezione

Trova i lati di questo triangolo rettangolo