La distribuzione binomiale

“Bi” significa “due” (come una bicicletta ha due ruote) … … quindi si tratta di cose con due risultati.,

Lasciate che il Lancio di una Moneta!

Lancia una moneta giusta tre volte … qual è la possibilità di ottenere due teste?,tr>

THH THT TTH TTT

Which outcomes do we want?,

“Due teste” potrebbero essere in qualsiasi ordine: “HHT”, “THH” e “HTH” hanno tutti due teste (e una coda).

Quindi 3 dei risultati producono “Due teste”.

Qual è la probabilità di ogni risultato?,zioni sono (P significa “Probabilità”):

• P(Tre Teste) = P(HHH) = 1/8
• P(a Due Teste) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Testa) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Zero Teste) = P(TTT) = 1/8

Possiamo scrivere questo in termini di una Variabile Casuale X = “numero di Teste da 3 lanci di una moneta”:

• P(X = 3) = 1/8
• P(X = 2) = 3/8
• P(X = 1) = 3/8
• P(X = 0) = 1/8

E questo è quello che sembra, come un grafico:

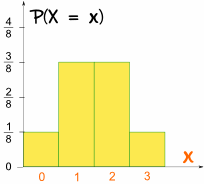
è simmetrica!,

Fare una formula

Ora immaginate che vogliamo le probabilità di 5 teste in 9 lanci: per elencare tutti i 512 risultati ci vorrà molto tempo!

Quindi facciamo una formula.

Nel nostro esempio precedente, come possiamo ottenere i valori 1, 3, 3 e 1 ?

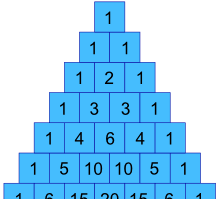
Beh, in realtà sono nel Triangolo di Pascal !

Possiamo farli usando una formula?

Certo che possiamo, ed eccolo qui:

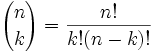
Viene spesso chiamato “n scegli k”

• n = numero totale
• k = numero che vogliamo
• il “!,”significa ” fattoriale”, ad esempio 4! = 1×2×3×4 = 24

Puoi leggere di più su di esso in Combinazioni e permutazioni.

Proviamolo:

Usiamolo per una domanda più difficile:

Bias!

Finora le probabilità di successo o fallimento sono state ugualmente probabili.

Ma cosa succede se le monete sono di parte (atterrare più su un lato di un altro) o scelte non sono 50/50.

Disegniamo un diagramma ad albero:

I casi “Due polli” sono evidenziati.

Le probabilità per “due polli” risultano essere 0,147, perché stiamo moltiplicando due 0,7 s e uno 0,3 in ciascun caso. In altre parole,

0.147 = 0.7 × 0.7 × 0.3

O, utilizzando esponenti:

= 0.72 × 0.31

0.7 è la probabilità di ogni scelta che si desidera chiamare p

Il 2 è il numero di scelte che si desidera chiamare k

E si ha (finora):

= pk × 0.31

“0”.,3 è la probabilità che la scelta opposta, in modo da è: 1−p

Il 1 è il numero di scelte opposte, in modo da è: n−k

Che ci dà:

= pk(1-p)(n-k)

Dove

• p è la probabilità di ogni scelta, vogliamo
• k è il numero di scelte che vuoi
• n è il numero totale di scelte

Ora sappiamo che la probabilità di ogni risultato è 0.147

OK. Questo è stato un sacco di lavoro per qualcosa che sapevamo già, ma ora abbiamo una formula che possiamo usare per domande più difficili.,

Mettendolo insieme

Ora sappiamo come calcolare quanti:

n!k!(n-k)!

E la probabilità di ciascuno:

pk(1-p)(n-k)

Quando moltiplicato insieme otteniamo:

Note importanti:

• Le prove sono indipendenti,
• Ci sono solo due possibili risultati ad ogni prova,
• La probabilità di “successo” ad ogni prova è costante.,

Quincunx

Gioca con Quincunx (quindi leggi Quincunx spiegato) per vedere la distribuzione Binomiale in azione.

Lancia il dado

Un dado equo viene lanciato quattro volte. Calcola le probabilità di ottenere:

• 0 Twos
• 1 Two
• 2 Twos
• 3 Twos
• 4 Twos

In questo caso n=4, p = P(Two) = 1/6

X è la Variabile casuale ‘Numero di Twos da quattro tiri’.,

Sostituire x = 0 a 4 nella formula:

P(k su n) = n!k!(n-k)! pk(1-p) (n-k)

In questo modo (fino a 4 cifre decimali):

Questa volta il grafico non è simmetrico:

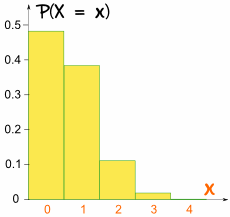
Non è simmetrico!

È distorta perché p non è 0.5

Biciclette sportive

La tua azienda produce biciclette sportive. il 90% passa l’ispezione finale (e il 10% fallisce e deve essere riparato).

Qual è la media e la varianza previste delle 4 ispezioni successive?

Per prima cosa, calcoliamo tutte le probabilità.,

• n = 4,
• p = P (Pass) = 0.9

X è la variabile casuale “Numero di passaggi da quattro ispezioni”.

Sostituire x = 0 a 4 nella formula:

P(k su n) = n!k!(n-k)! pk(1-p) (n-k)

Media, varianza e deviazione standard

Calcoliamo la media, la varianza e la deviazione standard per le ispezioni delle bici sportive.

Ci sono formule (relativamente) semplici per loro. Sono un po ‘ difficili da dimostrare, ma funzionano!,

La media, o “valore atteso”, è:

µ = np

la formula per La Varianza è:

Varianza σ2 = np(1-p)

E la Deviazione Standard è la radice quadrata della varianza:

σ = √(np(1-p))