la Statistica Bayesiana spiegato ai Principianti in inglese Semplice

Descrizione

• Gli svantaggi di frequentista statistiche portano alla necessità per la Statistica Bayesiana
• Scopri Statistica Bayesiana e Inferenza Bayesiana
• Ci sono vari metodi per testare la significatività del modello come il p-valore, intervallo di confidenza, ecc

Introduzione

Statistica Bayesiana continua a rimanere incomprensibile in combusta menti di molti analisti., Essendo stupito dall’incredibile potere dell’apprendimento automatico, molti di noi sono diventati infedeli alle statistiche. Il nostro obiettivo si è ristretto all’esplorazione dell’apprendimento automatico. Non è vero?

Non riusciamo a capire che l’apprendimento automatico non è l’unico modo per risolvere i problemi del mondo reale. In diverse situazioni, non ci aiuta a risolvere i problemi aziendali, anche se ci sono dati coinvolti in questi problemi. Per non dire altro, la conoscenza delle statistiche ti consentirà di lavorare su problemi analitici complessi, indipendentemente dalla dimensione dei dati.,

Nel 1770, Thomas Bayes introdusse il ‘Teorema di Bayes’. Anche dopo secoli più tardi, l’importanza delle “Statistiche bayesiane” non è svanita. Infatti, oggi questo argomento viene insegnato in grande profondità in alcune delle principali università del mondo.

Con questa idea, ho creato questa guida per principianti sulle statistiche bayesiane. Ho cercato di spiegare i concetti in modo semplicistico con esempi. È auspicabile una conoscenza preliminare della probabilità di base & statistiche., Si dovrebbe verificare questo corso per ottenere un basso completo su statistiche e probabilità.

Alla fine di questo articolo, avrai una comprensione concreta delle statistiche bayesiane e dei suoi concetti associati.,>Il Teorema di Bayes

Inferenza Bayesiana

• Bernoulli funzione di verosimiglianza
• Prima Convinzione di Distribuzione
• Posteriore convinzione di Distribuzione

Test per il Significato – Frequentista vs Bayesiano

• il p-valore
• Intervalli di Confidenza
• Fattore di Bayes
• Alta Densità Intervallo (ISU)

Prima di poter effettivamente scavare nella Statistica Bayesiana, cerchiamo di passare un paio di minuti la comprensione Frequentista Statistiche, la versione più popolare di statistiche la maggior parte di noi venire attraverso e di problemi inerenti a questo.,

Statistiche frequentiste

Il dibattito tra frequentisti e bayesiani ha ossessionato i principianti per secoli. Pertanto, è importante capire la differenza tra i due e come esiste una sottile linea di demarcazione!

È la tecnica inferenziale più utilizzata nel mondo statistico. Infatti, generalmente è la prima scuola di pensiero che una persona che entra nel mondo delle statistiche incontra.

Le statistiche dei frequentisti verificano se si verifica o meno un evento (ipotesi)., Calcola la probabilità di un evento nel lungo periodo dell’esperimento (cioè l’esperimento viene ripetuto nelle stesse condizioni per ottenere il risultato).

Qui vengono prese le distribuzioni di campionamento di dimensione fissa. Quindi, l’esperimento è teoricamente ripetuto un numero infinito di volte, ma praticamente fatto con un’intenzione di arresto. Ad esempio, eseguo un esperimento con un’intenzione di arresto in mente che interromperò l’esperimento quando viene ripetuto 1000 volte o vedo un minimo di 300 teste in un lancio di monete.

Andiamo più a fondo ora.,

Ora, capiremo le statistiche frequentiste usando un esempio di lancio della moneta. L’obiettivo è stimare l’equità della moneta. Di seguito è riportata una tabella che rappresenta la frequenza delle teste:

Sappiamo che la probabilità di ottenere una testa sul lancio di una moneta giusta è 0.5. No. of heads rappresenta il numero effettivo di testine ottenute. Difference è la differenza tra 0.5*(No. of tosses) - no. of heads.,

Una cosa importante è notare che, sebbene la differenza tra il numero effettivo di teste e il numero previsto di teste( 50% del numero di lanci) aumenti all’aumentare del numero di lanci, la proporzione tra numero di teste e numero totale di lanci si avvicina a 0,5 (per una moneta equa).

Questo esperimento ci presenta un difetto molto comune nell’approccio frequentista, cioè la dipendenza del risultato di un esperimento dal numero di volte in cui l’esperimento viene ripetuto.,

Per saperne di più sui metodi statistici frequentisti, puoi andare a questo eccellente corso sulle statistiche inferenziali.

I difetti intrinseci nelle statistiche frequentiste

Fino a qui, abbiamo visto solo un difetto nelle statistiche frequentiste. Beh, e ‘ solo l’inizio.

il 20 ° secolo ha visto un massiccio aumento delle statistiche frequentiste applicate ai modelli numerici per verificare se un campione è diverso dall’altro, un parametro è abbastanza importante da essere mantenuto nel modello e varialtre manifestazioni di test di ipotesi., Ma le statistiche frequentiste hanno subito alcuni grandi difetti nella sua progettazione e interpretazione che hanno posto una seria preoccupazione in tutti i problemi della vita reale. Ad esempio:

p-values misurato rispetto a una statistica campione (dimensione fissa) con alcune modifiche di intenzione di arresto con modifica dell’intenzione e della dimensione del campione. cioè se due persone lavorano sugli stessi dati e hanno un’intenzione di arresto diversa, possono ottenere due diversi p- values per gli stessi dati, il che è indesiderabile.,

Ad esempio: la persona A può scegliere di smettere di lanciare una moneta quando il conteggio totale raggiunge 100 mentre B si ferma a 1000. Per diverse dimensioni del campione, otteniamo diversi t-punteggi e diversi p-valori. Allo stesso modo, l’intenzione di fermarsi può cambiare dal numero fisso di lanci alla durata totale del lancio. Anche in questo caso, siamo tenuti a ottenere valori p diversi.

2 – Intervallo di confidenza (C. I) comep-value dipende fortemente dalla dimensione del campione., Ciò rende il potenziale di arresto assolutamente assurdo poiché non importa quante persone eseguano i test sugli stessi dati, i risultati dovrebbero essere coerenti.

3 – Gli intervalli di confidenza (CI) non sono distribuzioni di probabilità quindi non forniscono il valore più probabile per un parametro e i valori più probabili.

Questi tre motivi sono sufficienti per farti pensare agli svantaggi dell’approccio frequentista e perché c’è bisogno di un approccio bayesiano. Scopriamolo.,

Da qui, prima capiremo le basi delle statistiche bayesiane.

Statistica bayesiana

“Statistica bayesiana è una procedura matematica che applica le probabilità a problemi statistici. Fornisce alle persone gli strumenti per aggiornare le loro convinzioni nell’evidenza di nuovi dati.”

Hai capito? Mi spiego con un esempio:

Supponiamo che, su tutte le 4 gare di campionato (F1) tra Niki Lauda e James hunt, Niki abbia vinto 3 volte mentre James ne ha gestite solo 1.,

Quindi, se dovessi scommettere sul vincitore della prossima gara, chi sarebbe ?

Scommetto che diresti Niki Lauda.

Ecco la svolta. Che cosa succede se vi viene detto che ha piovuto una volta quando James ha vinto e una volta quando Niki ha vinto ed è certo che pioverà alla prossima data. Quindi, su chi scommetteresti i tuoi soldi ora ?

Per intuizione, è facile vedere che le possibilità di vincere per James sono aumentate drasticamente. Ma la domanda è: quanto ?,

Per capire il problema a portata di mano, dobbiamo familiarizzare con alcuni concetti, primo dei quali è la probabilità condizionale (spiegata di seguito).

Inoltre, ci sono alcuni pre-requisiti:

Pre-Requisiti:

1. Algebra lineare : per aggiornare le tue basi, puoi controllare l’Algebra dell’Accademia di Khan.
2. Probabilità e statistiche di base: Per aggiornare le vostre basi, è possibile controllare un altro corso da Khan Academy.

3.,1 Probabilità condizionale

È definita come: Probabilità di un evento A dato B uguale alla probabilità di B e A che accadono insieme diviso per la probabilità di B.”

Ad esempio: Assumere due insiemi parzialmente intersecanti A e B come mostrato di seguito.

Il set A rappresenta un insieme di eventi e il Set B ne rappresenta un altro. Vogliamo calcolare la probabilità di un dato B è già successo. Rappresentiamo l’evento dell’evento B ombreggiandolo con il rosso.,

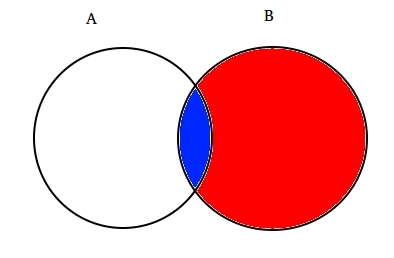
Ora da quando B è successo, la parte che ora conta per A è la parte ombreggiata in blu che è interessante . Così, la probabilità di A dato B risulta essere:

Quindi, possiamo scrivere la formula per il caso B dato Una si è già verificato da:

o

Ora, la seconda equazione può essere riscritta come :

Questo è noto come la Probabilità condizionata.,

Proviamo a rispondere a un problema di scommesse con questa tecnica.

Supponiamo, B essere l’evento di vincita di James Hunt. A essere l’evento di pioggia. Pertanto,

Sostituendo i valori nella formula della probabilità condizionale, otteniamo la probabilità di essere intorno al 50%, che è quasi il doppio del 25% quando la pioggia non è stata presa in considerazione (Risolvila alla tua fine).

Questo ha ulteriormente rafforzato la nostra convinzione di James vincente alla luce di nuove prove cioè pioggia., Ti starai chiedendo che questa formula assomigli molto a qualcosa di cui potresti aver sentito parlare molto. Pensa!

Probabilmente, hai indovinato bene. Sembra il teorema di Bayes.

Il teorema di Bayes si basa sulla probabilità condizionale e si trova nel cuore dell’inferenza bayesiana. Capiamolo in dettaglio ora.

3.2 Teorema di Bayes

Il Teorema di Bayes entra in vigore quando più eventi formano un insieme esaustivo con un altro evento B. Questo potrebbe essere compreso con l’aiuto del diagramma seguente.,

Ora, B può essere scritta come:

Così, la probabilità di B può essere scritto come

Ma

Così, in sostituzione di P(B) l’equazione della probabilità condizionata, otteniamo

Questa è l’equazione del Teorema di Bayes.

Inferenza bayesiana

Non ha senso immergersi nell’aspetto teorico di esso. Quindi, impareremo come funziona!, Prendiamo un esempio di lancio di monete per capire l’idea alla base dell’inferenza bayesiana.

Una parte importante dell’inferenza bayesiana è la creazione di parametri e modelli.

I modelli sono la formulazione matematica degli eventi osservati. I parametri sono i fattori nei modelli che influenzano i dati osservati. Ad esempio, nel lanciare una moneta, l’equità della moneta può essere definita come il parametro della moneta indicato da θ. Il risultato degli eventi può essere indicato da D.

Rispondi ora., Qual è la probabilità di 4 teste su 9 lanci (D) data l’equità della moneta (θ). cioè P(D|θ)

Aspetta, ho fatto la domanda giusta? No.

Ci dovrebbe essere più interessati a sapere : Dato un esito (D) qual è la probbaility di moneta fiera (θ=0.5)

Permette di rappresentare utilizzando il Teorema di Bayes:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

Qui P(θ) è la prima che ho.e la forza della nostra fede e l’imparzialità della moneta prima del lancio., È perfettamente giusto credere che la moneta possa avere un grado di equità tra 0 e 1.

P(D|θ) è la probabilità di osservare il nostro risultato data la nostra distribuzione per θ. Se sapessimo che la moneta era giusta, questo dà la probabilità di osservare il numero di teste in un particolare numero di lanci.

P(D) è la prova. Questa è la probabilità dei dati come determinata sommando (o integrando) tutti i possibili valori di θ, ponderati da quanto crediamo fortemente in quei particolari valori di θ.,

Se avessimo più viste di quale sia l’equità della moneta (ma non lo sapevamo per certo), allora questo ci dice la probabilità di vedere una certa sequenza di lanci per tutte le possibilità della nostra fede nell’equità della moneta.

P(θ|D) è la credenza posteriore dei nostri parametri dopo aver osservato le prove cioè il numero di teste.

Da qui, approfondiremo le implicazioni matematiche di questo concetto. Non preoccuparti. Una volta che li capisci, arrivare alla sua matematica è abbastanza facile.,

Per definire correttamente il nostro modello , abbiamo bisogno di due modelli matematici prima della mano. Uno per rappresentare la funzione di verosimiglianza P (D|θ) e l’altro per rappresentare la distribuzione delle credenze precedenti . Il prodotto di questi due dà la credenza posteriore P(θ|D) distribuzione.

Poiché prior e posterior sono entrambe credenze sulla distribuzione dell’equità della moneta, l’intuizione ci dice che entrambi dovrebbero avere la stessa forma matematica. Tienilo a mente. Ci torneremo di nuovo.,

Quindi, ci sono diverse funzioni che supportano l’esistenza del teorema di bayes. Conoscerli è importante, quindi li ho spiegati in dettaglio.

4.1. Bernoulli verosimiglianza funzione

Consente di ricapitolare ciò che abbiamo imparato sulla funzione di verosimiglianza. Quindi, abbiamo imparato che:

È la probabilità di osservare un particolare numero di teste in un particolare numero di lanci per una data equità di moneta. Ciò significa che la nostra probabilità di osservare teste/code dipende dall’equità della moneta (θ).,

P(y=1|θ)=

P(y=0|θ)=

Vale la pena notare che rappresentare 1 come teste e 0 come code è solo una notazione matematica per formulare un modello. Possiamo combinare le definizioni matematiche di cui sopra in un’unica definizione per rappresentare la probabilità di entrambi i risultati.

P(y/θ)=

Questa è chiamata Funzione di verosimiglianza di Bernoulli e il compito di lanciare monete è chiamato Prove di Bernoulli.,

y={0,1},θ=(0,1)

E quando si vuole vedere una serie di teste o di lancia, la sua probabilità è data da:

Inoltre, se ci sono interessati alla probabilità di un numero di capi z a girare in N numero di lanci, allora la probabilità è data da:

4.2. Previous Belief Distribution

Questa distribuzione viene utilizzata per rappresentare i nostri punti di forza sulle credenze sui parametri in base all’esperienza precedente.,

Ma, cosa succede se non si ha esperienza precedente?

Non preoccuparti. I matematici hanno ideato metodi per mitigare anche questo problema. È noto come uninformative priors. Vorrei informarvi in anticipo che è solo un termine improprio. Ogni priore uninformative fornisce sempre alcune informazioni evento la distribuzione costante prima.

Bene, la funzione matematica utilizzata per rappresentare le credenze precedenti è nota come beta distribution., Ha alcune proprietà matematiche molto belle che ci permettono di modellare le nostre convinzioni su una distribuzione binomiale.

La funzione di densità di probabilità della distribuzione beta è della forma:

dove, la nostra attenzione rimane sul numeratore. Il denominatore è lì solo per garantire che la funzione di densità di probabilità totale dopo l’integrazione valuti a 1.

αeβ sono chiamati i parametri di decisione della forma della funzione di densità., Qui αè analogo al numero di teste nelle prove eβ corrisponde al numero di code., Gli schemi di seguito vi aiuterà a visualizzare la distribuzione beta per diversi valori di α e β

È anche possibile disegnare la distribuzione beta per te utilizzando il seguente codice in R:

Nota: α e β sono intuitivi da capire perché si può essere calcolato conoscendo la media (µ) e la deviazione standard (s) della distribuzione., Infatti, essi sono correlati come:

Se media e deviazione standard di una distribuzione sono noti , allora ci parametri di forma possono essere facilmente calcolati.

Inferenza tracciata dai grafici sopra:

1. Quando non c’era lancio credevamo che ogni equità della moneta fosse possibile come raffigurato dalla linea piatta.
2. Quando c’era più numero di teste rispetto alle code, il grafico mostrava un picco spostato verso il lato destro, indicando una maggiore probabilità di teste e quella moneta non è giusta.,
3. Man mano che vengono fatti più lanci e le teste continuano a venire in proporzione maggiore, il picco si restringe aumentando la nostra fiducia nell’equità del valore del gettone.

4.3. Posterior Belief Distribution

La ragione per cui abbiamo scelto prior belief è ottenere una distribuzione beta. Questo perché quando lo moltiplichiamo con una funzione di verosimiglianza, la distribuzione posteriore produce una forma simile alla distribuzione precedente che è molto più facile da relazionare e capire., Se queste informazioni stuzzica l’appetito, sono sicuro che si è pronti a camminare un miglio in più.

Calcoliamo la credenza posteriore usando il teorema di bayes.

Calcolare posteriore credenza, usando il Teorema di Bayes,

Ora, la nostra posteriore fede diventa,

Questo è interessante., Conoscendo la distribuzione media e standard della nostra convinzione sul parametro θe osservando il numero di teste in N flip, possiamo aggiornare la nostra convinzione sul parametro del modello(θ).

Consente di capire questo con l’aiuto di un semplice esempio:

Supponiamo che tu pensi che una moneta sia di parte. Ha un bias medio (μ) di circa 0,6 con deviazione standard di 0,1.

Poi,

α= 13.8 , β=9.2

i.,e la nostra distribuzione sarà di parte sul lato destro. Supponiamo di aver osservato 80 teste (z=80) in 100 flip (N=100). Vediamo come la nostra prima e posteriore credenze stanno andando a guardare:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

Permette di visualizzare sia le credenze su di un grafico:

Il codice R per il grafico di cui sopra è, come:

}

Come più e più mortali sono fatti e nuovi dati osservati, le nostre convinzioni aggiornati., Questo è il vero potere dell’inferenza bayesiana.

Test for Significantity-Frequentist vs Bayesian

Senza entrare nelle rigorose strutture matematiche, questa sezione ti fornirà una rapida panoramica dei diversi approcci dei metodi frequentisti e bayesiani per testare il significato e la differenza tra i gruppi e quale metodo è più affidabile.

5.1. p-value

In questo, viene calcolato il punteggio t per un particolare campione da una distribuzione di campionamento di dimensioni fisse. Quindi, i valori p sono previsti., Possiamo interpretare i valori p come (prendendo un esempio di p-value come 0.02 per una distribuzione di media 100 ) : C’è il 2% di probabilità che il campione abbia media uguale a 100.

Questa interpretazione soffre del difetto che per le distribuzioni di campionamento di dimensioni diverse, si è tenuti ad ottenere un diverso t-score e quindi un diverso p-value. È completamente assurdo. Un valore p inferiore al 5% non garantisce che l’ipotesi nulla sia errata né un valore p superiore al 5% garantisce che l’ipotesi nulla sia corretta.

5.2., Anche gli intervalli di confidenza

soffrono dello stesso difetto. Inoltre, poiché C. I non è una distribuzione di probabilità , non c’è modo di sapere quali valori sono più probabili.

5.3. Il fattore di Bayes

Il fattore di Bayes è l’equivalente del valore p nel framework bayesiano. Consente di capire in modo completo.

L’ipotesi nulla nel quadro bayesiano assume ∞ distribuzione di probabilità solo ad un particolare valore di un parametro (diciamo θ=0.5) e una probabilità zero altrimenti dove., (M1)

L’ipotesi alternativa è che tutti i valori di θ siano possibili, quindi una curva piatta che rappresenta la distribuzione. (M2)

Ora, la distribuzione posteriore dei nuovi dati appare come di seguito.

Statistiche bayesiane rettificato credibilità (probabilità) di vari valori di θ. Si può facilmente vedere che la distribuzione di probabilità si è spostata verso M2 con un valore superiore a M1 cioè M2 è più probabile che accada.,

Il fattore di Bayes non dipende dai valori di distribuzione effettivi di θ ma dall’entità dello spostamento nei valori di M1 e M2.

Nel pannello A (mostrato sopra): la barra sinistra (M1) è la probabilità precedente dell’ipotesi nulla.

Nel pannello B (mostrato), la barra sinistra è la probabilità posteriore dell’ipotesi nulla.

Il fattore di Bayes è definito come il rapporto tra le quote posteriori e le quote precedenti,

Per rifiutare un’ipotesi nulla, si preferisce un BF<1/10.,

Possiamo vedere i benefici immediati dell’uso del fattore Bayes invece dei valori p poiché sono indipendenti dalle intenzioni e dalla dimensione del campione.

5.4. Intervallo ad alta densità (HDI)

HDI è formato dalla distribuzione posteriore dopo aver osservato i nuovi dati. Poiché HDI è una probabilità, il 95% HDI dà il 95% valori più credibili. È anche garantito che i valori del 95% si trovino in questo intervallo a differenza di C. I.

Nota, come il 95% HDI nella distribuzione precedente è più ampio della distribuzione posteriore del 95%., Questo perché la nostra fede in HDI aumenta dopo l’osservazione di nuovi dati.

Note finali

Lo scopo di questo articolo era quello di farti pensare al diverso tipo di filosofie statistiche là fuori e come nessuno di essi non può essere utilizzato in ogni situazione.

È giunto il momento che entrambe le filosofie siano unite per mitigare i problemi del mondo reale affrontando i difetti dell’altro., La parte II di questa serie si concentrerà sulle tecniche di riduzione della dimensionalità utilizzando algoritmi MCMC (Markov Chain Monte Carlo). La parte III si baserà sulla creazione di un modello di regressione bayesiana da zero e sull’interpretazione dei suoi risultati in R. Quindi, prima di iniziare con la Parte II, vorrei avere i tuoi suggerimenti / feedback su questo articolo.