In questa lezione, costruiremo i cinque (5) connettivi o operatori logici comuni. Sono considerati connettivi logici comuni perché sono molto popolari, utili e sempre insegnati insieme.
Prima di iniziare, ti suggerisco di rivedere la mia altra lezione in cui il link è mostrato di seguito.
Questa lezione introduttiva sulle tabelle di verità contiene conoscenze o informazioni prerequisite che ti aiuteranno a capire meglio il contenuto di questa lezione.,
Introduzione alle tabelle di verità, istruzioni e connettivi
I le iniziano elencando i cinque (5) connettivi logici comuni.
I Cinque (5) Comune Connettivi Logici o Operatori
- Negazione Logica
- Congiunzione Logica (E)
- Logica di Disgiunzione (Inclusiva O)
- Implicazione Logica (Condizionale)
- Logico Biconditional (Doppia Implicazione)
I., Tabella di verità della negazione logica
La negazione di un’istruzione è anche un’istruzione con un valore di verità esattamente opposto a quello dell’istruzione originale. Ad esempio, la negazione dell’istruzione è scritta simbolicamente come
~\large{P} o \large{\neg P}.
~{P} o {\neg P} è letto come “non P.”
Ricorda: L’operatore di negazione contrassegnato dal simbolo ~ o \neg prende il valore di verità dell’affermazione originaria poi uscita l’esatto opposto del suo valore di verità., In altre parole, la negazione inverte semplicemente il valore di verità di una determinata affermazione. Quindi, se l’istruzione P è vera, allora il valore di verità della sua negazione è falso. Allo stesso modo se P è falso il valore di verità della sua negazione è vero.

II. Tabella di verità della Congiunzione Logica
Una congiunzione è un tipo di istruzione composta, che si compone di due proposizioni (noto anche come semplici dichiarazioni), affiancati dall’operatore and.,
Il simbolo utilizzato per rappresentare l’operatore di congiunzione logica AND or è \color{red}\Large{\wedge}. Sembra una lettera invertita V.
Se abbiamo due semplici istruzioni P e Q, e vogliamo formare un’istruzione composta unita dall’operatore AND, possiamo scriverla come:
\large{P \wedge Q}.
{P \wedge Q} viene letto come “P e Q.”
Ricorda: il valore di verità dell’istruzione composta P \wedge Q è vero solo se i valori di verità P e Q sono entrambi veri., Altrimenti, P \ wedge Q è falso.
Si noti nella tabella di verità sottostante che quando P è vero e Q è vero, P \ wedge Q è vero. Tuttavia, le altre tre combinazioni di proposizioni P e Q sono false.

III. Tabella di verità della Disgiunzione Logica
Una disgiunzione è un tipo di istruzione composta, che si compone di due semplici dichiarazioni in formato unendo le dichiarazioni con l’operatore or.
In un’istruzione disgiunzione, l’uso di OR è inclusivo. Significa “uno o l’altro” o entrambi.,
Il simbolo utilizzato per rappresentare l’operatore di disgiunzione logica OR è \color{red}\Large{ \vee }. Assomiglia alla lettera V dell’alfabeto.
Due proposizioni P e Q unite dall’operatore OR per formare un’istruzione composta sono scritte come:
\large{P \vee Q}.
{P \vee Q} viene letto come “P o Q.”
Ricorda: il valore di verità dell’istruzione composta P \vee Q è vero se il valore di verità delle due semplici istruzioni P e Q è vero., Inoltre, P \vee Q è vero anche quando i valori di verità di entrambe le affermazioni P e Q sono veri. Tuttavia, l’unica volta che l’istruzione disgiunzione P \vee Q è falsa, accade quando i valori di verità di P e Q sono falsi.
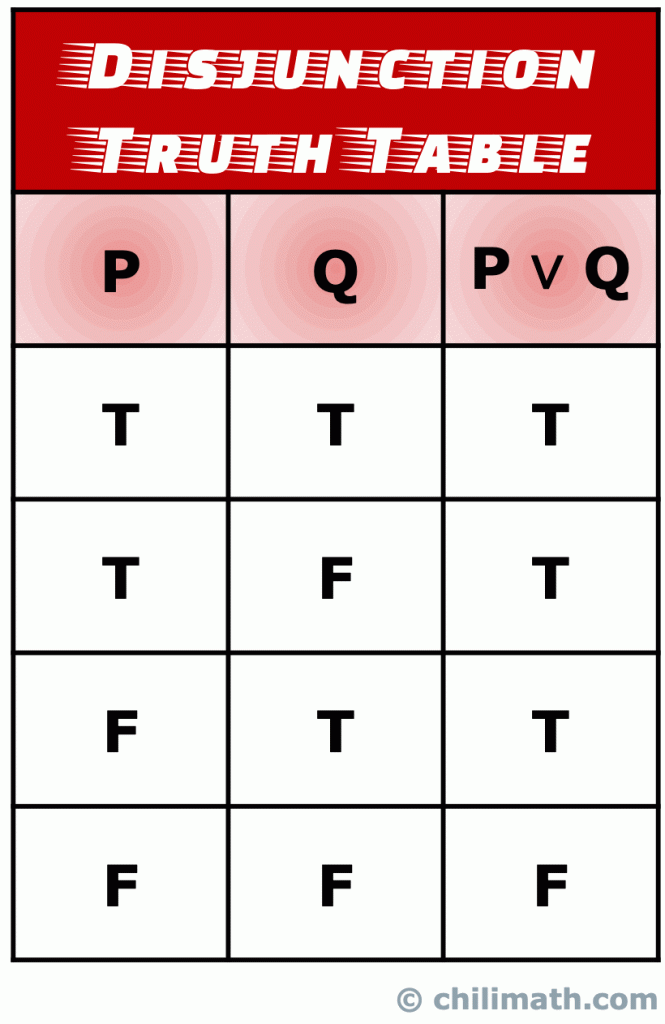
IV. Tabella di verità dell’Implicazione Logica
Un’implicazione (noto anche come una istruzione condizionale) è un tipo di istruzione composta, che è formata dall’unione di due semplici dichiarazioni con l’implicazione logica connettivo o operatore.,
Il simbolo che viene utilizzato per rappresentare l’operatore di implicazione logica è una freccia che punta a destra, quindi una freccia verso destra.

Quando due semplici enunciati P e Q sono uniti da l’implicazione operatore, abbiamo:
\Large{P \in Q}.
- dove P è conosciuta come l’ipotesi
- dove Q è conosciuta come la conclusione
Ci sono molti modi per leggere il condizionale {P \a Q}., Di seguito sono riportati alcuni dei pochi comuni.
Ricorda: il valore di verità dell’istruzione composta da P \a Q è vero quando entrambe le semplici istruzioni P e Q sono vere. Moreso, P \ a Q è sempre vero se P è falso. L’unico scenario che da P \a Q è falso si verifica quando P è vero e Q è falso.
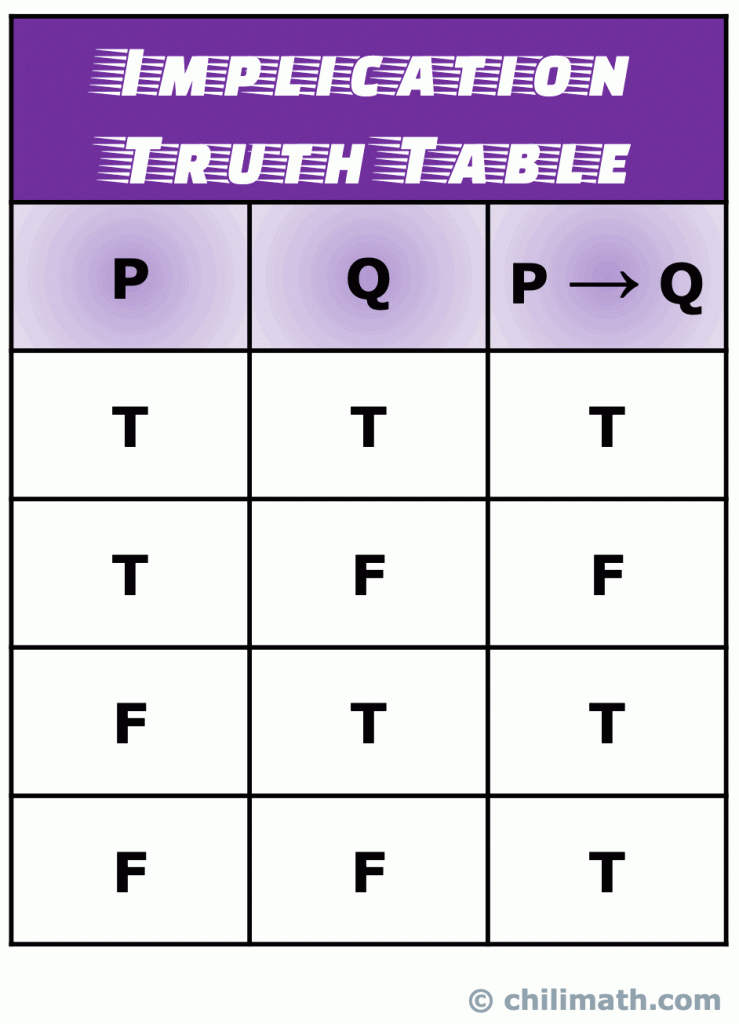
V., Tabella di verità della logica bicondizionale o doppia implicazione
Una doppia implicazione (nota anche come istruzione bicondizionale) è un tipo di istruzione composta che si forma unendo due semplici istruzioni con l’operatore bicondizionale. Un’istruzione bicondizionale è in realtà una combinazione di un’istruzione condizionale e il suo contrario.
L’operatore bicondizionale è indicato da una freccia a due punte.,

Quando si uniscono due semplici dichiarazioni (noto anche come molecolari dichiarazioni) con il biconditional operatore, si ottiene:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} viene letto come “P se e solo se D.,”
- dove P è noto come l’antecedente
- dove Q è noto come il conseguente
Ricorda: Il valore di verità dell’istruzione bicondizionale P \leftrightarrow Q è vero quando entrambe le semplici istruzioni P e Q sono entrambe vere o entrambe false. Altrimenti, P \ leftrightarrow Q è false.
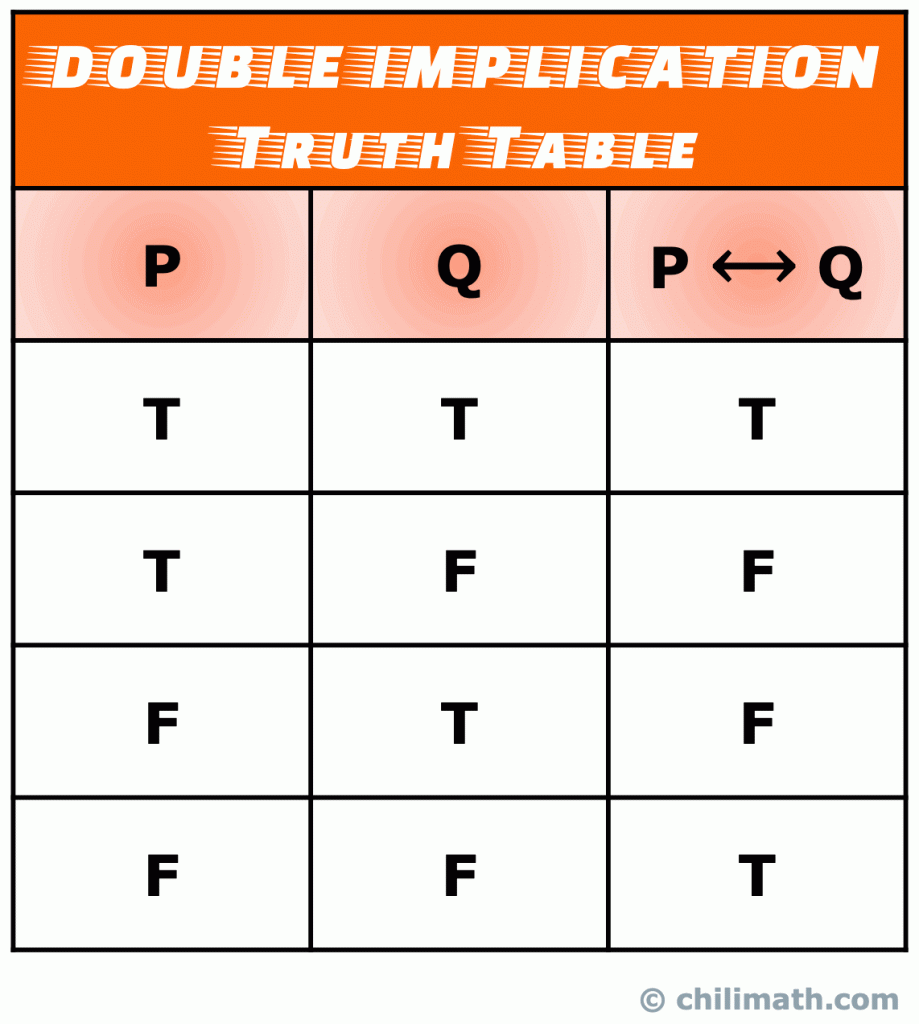
Potresti essere interessato anche a:
Introduzione a tabelle di verità, istruzioni e connettivi logici
Converse, Inverse e Contrappositive di una dichiarazione condizionale
Lascia un commento