Teoria molecolare cinetica dei gas

Pressione e KMT

I fenomeni macroscopici della pressione possono essere spiegati in termini di teoria molecolare cinetica dei gas. Supponiamo il caso in cui una molecola di gas (rappresentata da una sfera) si trovi in una scatola, lunghezza L (Figura 1). Usando le ipotesi di cui sopra, e considerando che la sfera si muove solo nella direzione x, possiamo esaminare l’istanza della sfera che si scontra elasticamente con una delle pareti della scatola.,

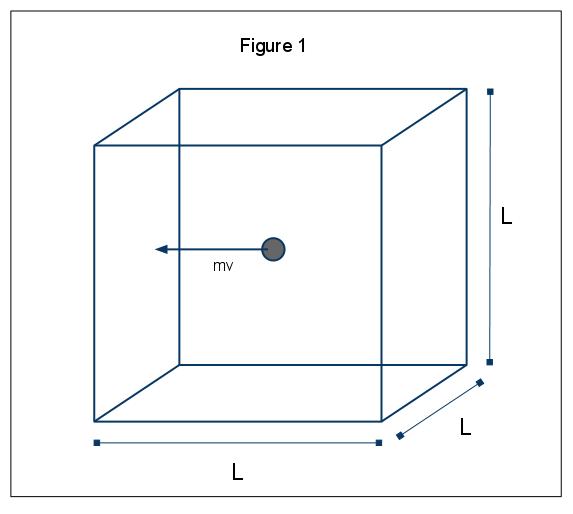
Il momento di questa collisione è dato da p=mv, in questo caso p=mvx, dato che stiamo considerando solo la dimensione x. La variazione totale della quantità di moto per questa collisione è quindi data da

\

Dato che la quantità di tempo che impiega tra le collisioni della molecola con la parete è L/vx possiamo dare la frequenza delle collisioni della molecola contro una data parete della scatola per unità di tempo come vx/2L., Si può ora risolvere per il cambiamento di quantità di moto per unità di tempo:

\

Risolvere per quantità di moto per unità di tempo dà la forza esercitata da un oggetto (F=ma=p/tempo)., Con l’espressione F=mvx2/L adesso si può risolvere per la pressione esercitata dalla collisione molecolare, dove l’area è data come la superficie di una parete del box, A=L2:

\

\

L’espressione ora può essere scritto in termini di pressione associati con le collisioni da un numero N di molecole:

\

Questa espressione può ora essere rettificato per tener conto per il movimento in x, y e z le indicazioni usando mean-square velocità per tre dimensioni e un grande valore di n., L’espressione ora è scritta come:

\

Questa espressione ora dà pressione, una qualità macroscopica, in termini di moto atomico. Il significato della relazione di cui sopra è che la pressione è proporzionale alla velocità media quadrata delle molecole in un dato contenitore. Pertanto, all’aumentare della velocità molecolare aumenta anche la pressione esercitata sul contenitore.