Oversikt
- ulempene av frequentist statistikk føre til behov for Bayesiansk Statistikk
- Oppdag Bayesiansk Statistikk og Bayesiansk Inferens
- Det finnes ulike metoder for å teste betydningen av modellen som p-verdi, konfidensintervall, etc.
Innledning
Bayesiansk Statistikk fortsetter å forbli uforståelig i den tente hodet av mange analytikere., Bli overrasket av den utrolige kraften av maskinlæring, mange av oss har blitt utro mot statistikk. Vårt fokus har snevret til å utforske maskinlæring. Er ikke det sant?
Vi ikke klarer å forstå at maskinen læring er ikke den eneste måten å løse virkelige problemer. I flere situasjoner, vil det ikke hjelpe oss med å løse forretningsproblemer, selv om det er data som er involvert i disse problemene. For å si det mildt, kunnskap om statistikk vil tillate deg å arbeide på kompliserte analytiske problemer, uavhengig av størrelsen på dataene.,
I 1770-tallet, Thomas Bayes introdusert ‘Bayes Teorem’. Selv etter århundrer senere, betydningen av ‘Bayesiansk Statistikk’ har ikke bleknet bort. Faktisk, i dag dette emnet blir undervist på store dyp i noen av verdens ledende universiteter.
Med denne ideen, har jeg laget denne beginner ‘ s guide på Bayesiansk Statistikk. Jeg har prøvd å forklare begrepene på en forenklet måte med eksempler. Forkunnskaper grunnleggende sannsynlighet & statistikk er ønskelig., Du bør sjekke ut dette emnet for å få et helhetlig lave ned på statistikk og sannsynlighet.
Ved slutten av denne artikkelen, vil du ha en konkret forståelse av Bayesiansk Statistikk og tilhørende begreper.,>Bayes Teorem
- Bernoulli sannsynligheten funksjon
- Før Troen Distribusjon
- Posterior tro Distribusjon
- p-verdi
- konfidensintervaller
- Bayes Faktor
- Høy Tetthet Intervall (HDI)
Før vi faktisk fordype deg i Bayesiansk Statistikk, la oss bruke et par minutter forståelse Frequentist Statistikk, mer populære versjonen av statistikk som de fleste av oss kommer over og den iboende problemer i det.,
Frequentist Statistikk
debatten mellom frequentist og bayesiansk har hjemsøkt nybegynnere i århundrer. Derfor er det viktig å forstå forskjellen mellom de to, og hvordan fungerer det eksisterer en tynn linje for avgrensning!
Det er den mest brukte slutnings-teknikk i statistisk verden. Infact, generelt det er første skole med tanke på at en person går inn i statistikken verden kommer over.
Frequentist Statistikk tester om en hendelse (hypotese) oppstår eller ikke., Det beregner sannsynligheten for at en hendelse i det lange løp av eksperimentet (jeg.e eksperimentet gjentas under samme forhold for å oppnå resultatet).
Her prøvetaking fordelingen av fast størrelse er tatt. Så, eksperimentet er teoretisk gjentatt uendelig antall ganger, men praktisk talt ferdig med en intensjon om å stoppe. Jeg kan For eksempel utføre et eksperiment med en intensjon om å stoppe i tankene at jeg vil stoppe eksperimentet når det gjentas 1000 ganger eller jeg ser minimum 300 hoder i et myntkast.
La oss gå dypere nå.,
Nå, vil vi forstå frequentist statistikk ved hjelp av et eksempel på myntkast. Målet er å anslå den rettferdighet av mynten. Nedenfor er en tabell som representerer frekvens av hoder:

Vi vet at sannsynligheten for å få et hode på å kaste en mynt er 0.5. No. of heads representerer den faktiske antall hoder innhentet. Difference er forskjellen mellom 0.5*(No. of tosses) - no. of heads.,
En viktig ting å merke seg at, selv om forskjellen mellom det faktiske antall hoder og forventet antall hoder( 50% av antall kaster) øker antall av kaster er økt, har andelen av antall hoder til totalt antall kaster tilnærminger 0.5 (for en rettferdig mynt).
Dette eksperimentet presenterer oss med en veldig vanlig feil er funnet i frequentist tilnærming dvs. Avhengighet av resultatet av et eksperiment på hvor mange ganger eksperimentet gjentas.,
Hvis du vil vite mer om frequentist statistiske metoder, kan du ta turen til denne utmerkede kurs på slutningsstatistikk.
Iboende Feil i Frequentist Statistikk
Till her, vi har sett bare en feil i frequentist statistikk. Vel, det er bare begynnelsen.
20. århundre var det et enormt oppsving i frequentist statistikk blir brukt til å numeriske modeller for å sjekke om en prøve er forskjellig fra de andre, en parameter som er viktig nok til å bli holdt i modellen og variousother manifestasjoner av hypotesetesting., Men frequentist statistikk lidd noen store feil i sin utforming og fortolkning som utgjorde en alvorlig bekymring i alle virkelige problemer. For eksempel:
p-values målt mot et eksempel (fast størrelse) statistikk med noen intensjon om å stoppe endringer med endring i intensjon og utvalgsstørrelsen. jeg har.e Hvis to personer jobber på de samme data og har ulike stoppe intensjon, de kan få to forskjellige p- values for de samme dataene, som er uønsket.,
For eksempel: Person A kan velge å slutte å kaste en mynt når det totale antallet har nådd 100 mens B stopper på 1000. For eksempel ulike størrelser, får vi forskjellige t-score og ulike p-verdier. På samme måte intensjon om å stoppe de kan endres fra fast antall knipser til total varighet av bla. I denne saken også, vi er nødt til å få ulike p-verdier.
2 – konfidensintervall (C. jeg) liker p-value er svært avhengig av prøvestørrelsen., Dette gjør stoppe potensielle helt absurd siden ingen rolle hvor mange mennesker utføre tester på de samme dataene, resultatene bør være konsekvent.
3 – konfidensintervaller (C. jeg) er ikke sannsynlighetsfordelinger derfor de ikke gir den mest sannsynlig verdi for en parameter, og den mest sannsynlige verdier.
Disse tre grunnene er nok til å få deg til å gå inn å tenke på ulempene av frequentist tilnærming og hvorfor er det et behov for bayesiansk tilnærming. La oss finne det ut.,
Fra her, vil vi først forstå det grunnleggende om Bayesiansk Statistikk.
Bayesiansk Statistikk
«Bayesiansk statistikk er en matematisk prosedyren som gjelder sannsynligheten for å statistiske problemer. Det gir folk verktøy for å oppdatere sin tro bevis av nye data.»
Du fikk det? La meg forklare det med et eksempel:
Antar, ut av alle de 4 mesterskapet løp (F1) mellom Niki Lauda og James hunt, Niki vant 3 ganger, mens James klarte bare 1.,
Så, hvis du var å satse på den som vinner neste løp, som ville han være ?
jeg vedder på at du ville si Niki Lauda.
Her er vri. Hva hvis du blir fortalt at det regnet en gang når James vant, og når Niki vant, og det er klart at det blir regn på neste date. Så, hvem ville du satse pengene dine på nå ?
Ved hjelp av intuisjon, det er lett å se at sjansene for å vinne for James har økt drastisk. Men spørsmålet er: hvor mye ?,
for Å forstå problemet på hånden, vi trenger å bli kjent med noen begreper, for det første som er betinget sannsynlighet (forklart nedenfor).
I tillegg er det visse forutsetninger:
Forutsetninger:
- Lineær Algebra : Hvis du vil oppdatere din grunnleggende, du kan sjekke ut Khan Academy Algebra.
- Sannsynlighet og Grunnleggende Statistikk : Hvis du vil oppdatere din grunnleggende, du kan sjekke ut en annen kurs med Khan Academy.
3.,1 Betinget Sannsynlighet
Det er definert som: Sannsynligheten for en hendelse A gitt B er lik sannsynligheten for B og En happening sammen dividert med sannsynligheten for B.»
For eksempel: Anta to delvis kryssende settene A og B, som vist nedenfor.
Angi En representerer ett sett av hendelser og Sett B representerer en annen. Vi ønsker å beregne sannsynligheten for A gitt B som allerede har skjedd. Lar representerer skjer av hendelse B av skyggelegging det med rødt.,
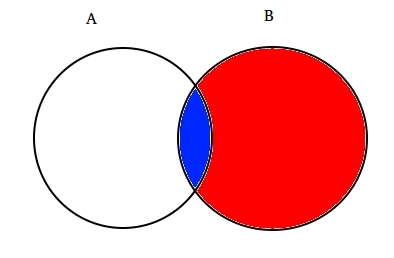
Nå, siden B har skjedd, det som nå teller for En er en del skyggelagt i blått som er interessant ![]() . Så sannsynligheten for A gitt B viser seg å være:
. Så sannsynligheten for A gitt B viser seg å være:
Derfor, vi kan skrive formelen for hendelsen B gitt En allerede oppstått ved:
eller
Nå, i den andre ligningen kan skrives om slik :
Dette er kjent som Betinget Sannsynlighet.,
La oss prøve å svare på en betting problemet med denne teknikken.
Tenk, B være tilfelle av gevinst av James Hunt. En være tilfelle regn. Derfor,
Erstatte verdier i den betingede sannsynligheten formelen, får vi sannsynligheten for å være rundt 50%, som er nesten det dobbelte av 25% når regnet ikke ble tatt hensyn til (Løse det på slutten).
Dette ytterligere styrket vår tro på James vinne i lys av nye bevis jeg.e regn., Du må være lurer på at denne formelen bærer nær likhet med noe du har kanskje hørt mye om. Tror!
Sannsynligvis, du gjettet det rett. Det ser ut som Bayes Teorem.
Bayes teorem er bygget på toppen av betinget sannsynlighet, og ligger i hjertet av Bayesiansk Inferens. La oss forstå det i detalj nå.
3.2 Bayes Teorem
Bayes Teorem trer i kraft når flere hendelser danne et uttømmende sett med en annen hendelse B. Dette kan forstås ved hjelp av diagrammet nedenfor.,

Nå, B kan skrives som
Så, sannsynligheten for at B kan skrives som,
, Men![]()
Så, sette P(B) i ligningen for betinget sannsynlighet får vi

Dette er ligningen av Bayes Teorem.
Bayesiansk Inferens
Det er ingen vits i å dykke inn i den teoretiske aspektet av det. Så, vi vil vite hvordan det fungerer!, La oss ta et eksempel på mynt kaste å forstå ideen bak bayesiansk inferens.
En viktig del av bayesiansk inferens er etablering av parametere og modeller.
– Modeller er den matematiske formuleringen av den observerte hendelser. Parametrene er de faktorer i modellene som påvirker den observerte data. For eksempel, i å kaste en mynt, rettferdighet av mynten kan være definert som parameter av mynt merket med θ. Utfallet av hendelsene kan være merket med D.
Svar på dette nå., Hva er sannsynligheten for 4 hoder av 9 kaster(D) gitt rettferdighet av mynt (θ). jeg har.e P(D|θ)
Vent, gjorde jeg stiller de riktige spørsmål? Ingen.
Vi bør være mer interessert i å vite : Gitt et utfall (D) hva er probbaility av mynt blir rettferdig (θ=0.5)
Kan representere det ved hjelp av Bayes Teorem:
P(θ|D)=(P(D|θ) X P(θ))/P(D)
Her P(θ) er før jeg.e styrken i vår tro på rettferdigheten av mynt før du kaster., Det er helt greit å tro at mynt kan ha noen som helst grad av rettferdighet mellom 0 og 1.
P(D|θ) er sannsynligheten for å observere våre resultat med tanke på vår distribusjon for θ. Hvis vi visste at mynten var virkelig, dette gir sannsynligheten for å observere antall hoder i et bestemt antall flips.
P(D) er bevis. Dette er sannsynligheten for data som bestemmes ved å summere (eller integrere) på tvers av alle mulige verdier av θ, vektet etter hvor sterkt vi tror på de bestemte verdier av θ.,
Hvis vi hadde flere visninger av hva rettferdighet av mynten er (men ikke vet sikkert), da dette forteller oss at sannsynligheten for å se en bestemt sekvens av knipser for alle muligheter på vår tro på at mynten er rettferdig.
P(θ|D) er den posteriore troen på våre parametre etter å ha observert bevis jeg.e antall hoder .
her Fra, vi skal dykke dypere inn i matematiske implikasjoner av dette konseptet. Ikke bekymre deg. Når du forstår dem, å komme til sin matematikk er ganske enkel.,
for Å definere vår modell riktig , trenger vi to matematiske modeller før hånd. En til å representere sannsynligheten funksjon P(D|θ) og de andre for å representere fordelingen av tidligere oppfatninger . Produktet av disse to gir bakre tro P(θ|D) fordeling.
Siden før og posterior er både oppfatninger om fordeling av rettferdighet av mynt, intuisjon forteller oss at begge skal ha samme matematisk form. Holde dette i bakhodet. Vi vil komme tilbake til det igjen.,
Så, det er flere funksjoner som støtter eksistensen av bayes teorem. Kjenne dem er viktig, derfor jeg har forklart dem i detalj.
4.1. Bernoulli sannsynligheten funksjon
Kan gå gjennom hva vi har lært om sannsynligheten funksjon. Så, vi lærte at:
Det er sannsynligheten for å observere et bestemt antall hoder i et bestemt antall knipser for en gitt rettferdighet av mynten. Dette betyr at våre sannsynligheten for å observere krone/mynt, avhenger av rettferdighet av mynt (θ).,
P(y=1|θ)=
P(y=0|θ)=
Det er verdt å merke seg at som representerer 1 som hoder og 0 som haler er bare en matematisk notasjon for å formulere en modell. Vi kan kombinere ovenfor matematiske definisjoner i en enkelt definisjon representerer sannsynligheten for at begge utfallene.
P(y|θ)=
Dette kalles Bernoulli Sannsynligheten Funksjon og oppgave av mynt flipping kalles bernoullis prøvelser.,
y={0,1},θ=(0,1)
Og, når vi ønsker å se en serie krone eller vipper, dens sannsynlighet er gitt ved:
Videre, hvis vi er interessert i sannsynligheten for antall hoder z slå opp i N antall knipser så sannsynligheten er gitt ved:
4.2. Før Troen Distribusjon
Denne fordelingen er brukt til å representere våre styrker på oppfatninger om parametre basert på tidligere erfaring.,
Men, hva hvis man ikke har noen tidligere erfaring?
ikke bekymre deg. Matematikere har utviklet metoder for å redusere dette problemet også. Det er kjent som uninformative priors. Jeg ønsker å informere deg på forhånd at det er bare en misvisende benevnelse. Hver uninformative før alltid gir noen informasjon om arrangementet konstant fordeling før.
Vel, det matematisk funksjon som brukes til å representere før livssyn er kjent som beta distribution., Den har noen veldig fine matematiske egenskaper som gjør oss i stand til å modellere våre forestillinger om en binominal distribusjon.
sannsynlighetstetthetsfunksjonen av beta-fordelingen er på formen :
hvor er vårt fokus forblir på telleren. Nevneren er det bare å sikre at den totale sannsynlighetstetthetsfunksjonen på integrering evaluerer til 1.
α og β kalles formen bestemme parametre av tetthet og funksjon., Her α er analogt til antall hoder i prøvelser og β tilsvarer antall mynt., Tegningen nedenfor vil hjelpe deg å visualisere beta-fordelinger for ulike verdier av α og β

Du kan også tegne beta-distribusjon for deg selv ved hjelp av følgende kode i R:
Merk: α og β er intuitive å forstå siden de kan beregnes ved å vite gjennomsnitt (ĩ) og standardavvik (σ) for distribusjon., Faktisk, de er i slekt som :
Hvis du mener og standardavvik av en distribusjon er kjent for , så er det formen parametere kan lett beregnes.
Slutning trekkes fra grafene over:
- Når det ikke var kaste trodde vi at hver rettferdighet av mynten er mulig som avbildet av flat linje.
- Når det var flere antall hoder enn de haler, grafen viste en topp forskjøvet mot høyre, noe som indikerer høyere sannsynlighet for kron og mynt som ikke er rettferdig.,
- Som mer kaster er gjort, og heads fortsetter å komme i større andel toppen smalner øke vår tillit i rettferdighet av mynt verdi.
4.3. Posterior Tro Distribusjon
grunnen Til at vi valgte før tro er å få tak i en beta-fordelingen. Dette er fordi når vi multiplisere det med en likelihood-funksjon, posterior distribusjon gir en form lik den før distribusjon som er mye lettere å forholde seg til og forstå., Hvis dette mye informasjon whets appetitten, jeg er sikker på at du er klar til å gå en ekstra mil.
La oss beregne posterior tro ved hjelp av bayes teorem.
Beregning av posterior tro ved hjelp av Bayes Teorem
Nå, vår bakre tro blir,
Dette er interessant., Bare å vite at de betyr og standard distribusjon av vår tro om parameteren θ og ved å observere antall hoder i N knipser, vi kan oppdatere våre tro om det-modell parameter(θ).
Kan forstå dette med hjelp av et enkelt eksempel:
la oss Anta at du mener at en mynt er partisk. Det har et gjennomsnitt (ĩ) slagside på rundt 0.6 med standard avvik på 0,1.
Så ,
α= 13.8 , β=9.2
jeg.,e vår distribusjon vil være forutinntatt på høyre side. La oss anta at du observert 80 hoder (z=80) i 100 knipser(N=100). La oss se hvordan våre før og posterior tro kommer til å se:
prior = P(θ|α,β)=P(θ|13.8,9.2)
Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)
Kan visualisere både tro på en graf:

R-kode for den grafen som er:
}
Som mer og mer knipser er gjort og nye data er observert, vår tro bli oppdatert., Dette er den virkelige kraften i Bayesiansk Analyse.
Test for Betydning – Frequentist vs Bayesiansk
Uten å gå inn i den strenge matematiske strukturer, denne delen vil gi deg en rask oversikt over ulike tilnærminger til frequentist og bayesianske metoder for å teste for betydning, og forskjellen mellom grupper og hvilken metode som er mest pålitelig.
5.1. p-verdi
I dette, t-score for en enkelt prøve fra en prøvetaking distribusjon av fast størrelse er beregnet. Så, p-verdier er spådd., Vi kan tolke p-verdier som (ta et eksempel p-verdi 0,02 for en fordeling av gjennomsnittlig 100) : Det er 2% sannsynlighet for at prøven må bety lik 100.
Denne tolkningen lider av feil som for prøvetaking fordelingen av ulike størrelser, og en er nødt til å få forskjellige t-score og dermed ulike p-verdi. Det er helt absurd. En p-verdi mindre enn 5% ikke garantere at nullhypotesen er feil eller en p-verdi som er større enn 5% sørger for at nullhypotesen er riktig.
5.2., Konfidensintervaller
konfidensintervaller også lider av samme feil. Videre siden C. jeg er ikke en sannsynlighetsfordeling , det er ingen måte å vite hvilke verdier som er mest sannsynlig.
5.3. Bayes Faktor
Bayes faktor er tilsvarende p-verdi i bayesiansk rammeverk. Kan forstå det på en helhetlig måte.
nullhypotesen i bayesiansk rammeverk forutsetter ∞ sannsynlighetsfordeling bare ved en bestemt verdi på en parameter (si θ=0.5) og en null sannsynlighet annet der., (M1)
Den alternative hypotesen er at alle verdier av θ er mulig, derav en flat kurve som representerer distribusjon. (M2)
Nå, posteriore fordelingen av de nye dataene ser ut som nedenfor.

Bayesiansk statistikk justert troverdighet (sannsynlighet) for ulike verdier av θ. Det kan være lett å se at sannsynligheten fordelingen er forskjøvet mot M2 med en høyere verdi enn M1 jeg.e M2 er mer sannsynlig til å skje.,
Bayes faktoren ikke er avhengig av den faktiske fordelingen verdier av θ, men omfanget av skift i verdier av M1 og M2.
I panel A (vist ovenfor): venstre linjen (M1) er den tidligere sannsynlighet for at nullhypotesen.
I panel B (vist), venstre bar er den posteriore sannsynlighet for at nullhypotesen.
Bayes faktor er definert som forholdet mellom den bakre sjanser til før odds,
for Å forkaste nullhypotesen, en BF <1/10 er foretrukket.,
Vi kan se den umiddelbare fordelene ved å bruke Bayes Faktor i stedet for p-verdier siden de er uavhengig av intensjoner og utvalgsstørrelse.
5.4. Høy Tetthet Intervall (HDI)
HDI er dannet fra den posteriore fordelingen etter å ha observert de nye dataene. Siden HDI er en sannsynlighet på 95% HDI gir 95% mest troverdige verdier. Det er også garantert at 95% av verdiene vil ligge i dette intervallet i motsetning til C. I.
Merke, hvor 95% HDI i før distribusjon er bredere enn 95% posterior distribusjon., Dette er fordi vår tro på HDI-verdien øker ved observasjon av nye data.

Avslutt Notater
målet med denne artikkelen var å få deg til å tenke på annen type statistisk filosofier finnes der ute og hvordan noen enkelt av dem kan ikke brukes i en hver situasjon.
Det er på høy tid at både filosofier er slått sammen for å løse virkelige problemer ved å ta feil av de andre., Del II av denne serien vil fokusere på Dimensionality Reduksjon teknikker ved hjelp av MCMC (Markov Chain Monte Carlo) algoritmer. Del III vil være basert på å skape en Bayesiansk regresjon modell fra bunnen av og å tolke resultatene i R. Så, før jeg starter med Del II, jeg vil gjerne ha ditt forslag / tilbakemelding på denne artikkelen.
Legg igjen en kommentar