Den Binomiske Fordelingen

«Bi» betyr «to» (som en sykkel har to hjul) … … så dette er om ting med to resultatene.,

La oss Kaste en Mynt!

Kaste en mynt tre ganger … hva er sjansen for å få to Hoder?,tr>

THH THT TTH TTT

Which outcomes do we want?,

«To Hoder» kan være i hvilken som helst rekkefølge: «HHT», «THH» og «HTH» alle har to Hoder (og en Hale).

Så 3 av resultatene produsere «To Hoder».

Hva er sannsynligheten for hvert utfall?,kravspesifikasjoner er (S) betyr «Sannsynligheten for»):

• P(Tre Hoder) = P(HHH) = 1/8
• P(To Hoder) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
• P(En Leder) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Null Hoder) = P(T) = 1/8

Vi kan skrive dette i form av en Tilfeldig Variabel, X = «antall» Hoder fra 3 kaster en mynt»:

• P(X = 3) = 1/8
• P(X = 2) = 3/8
• P(X = 1) = 3/8
• P(X = 0) = 1/8

Og dette er hva det ser ut som en graf:

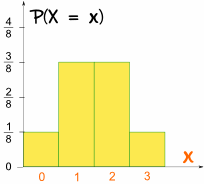
Det er symmetrisk!,

å Lage en Formel

Nå forestille vi vil sjansene for 5 hoder i 9 kaster: for å liste alle 512 resultater vil ta lang tid!

Så la oss lage en formel.

I vår forrige eksempel, hvordan kan vi få verdiene 1, 3, 3 og 1 ?

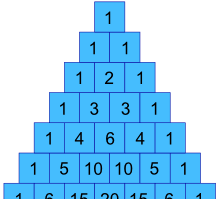
Vel, de er faktisk i Pascal ‘ s Trekant !

Kan vi lage dem ved hjelp av en formel?

Sikker på at vi kan, og her er det:

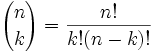
Det er ofte kalt «n velge k»

• n = totalt antall
• k = antall vi ønsker
• «!,»betyr «fakultet», for eksempel 4! = 1×2×3×4 = 24

Du kan lese mer om det på Kombinasjoner og Permutasjoner.

La oss prøve det:

La oss bruke den for et vanskeligere spørsmål:

Bias!

Så langt sjansene for suksess eller fiasko har vært like sannsynlige.

Men hva hvis myntene er partisk (lande mer på en side enn en annen) eller valg er ikke 50/50.

La oss tegne et tre-diagram:

«To Chicken» tilfeller er uthevet.

sannsynlighetene for «to kyllinger» alt arbeid ut til å være 0.147, fordi vi er å multiplisere to 0.7 s og ett 0.3 i hvert enkelt tilfelle. Med andre ord

0.147 = 0.7 × 0.7 × 0.3

Eller, ved hjelp av eksponenter:

= 0.72 × 0.31

0.7 er sannsynligheten for hvert valg vi vil, kan du ringe det s

2 er Det mange valg vi vil, kan du ringe det k

– Og vi har (så langt):

= pk × 0.31

0.,3 er sannsynligheten for det motsatte valget, så det er: 1−p

1 er antall motsatt valg, så det er: n−k

Som gir oss:

= pk(1-p)(n-k)

Hvor

• p er sannsynligheten for hvert valg vi ønsker
• k er antall valg vi ønsker
• n er det totale antall valg

Nå vet vi at sannsynligheten for hvert utfall er 0.147

OK. Det var mye arbeid for noe vi visste allerede, men nå har vi en formel som vi kan bruke for vanskeligere spørsmål.,

Setter det Sammen

Nå vet vi hvordan vi skal beregne hvor mange:

n!k!(n-k)!

Og sannsynligheten for at hver:

pk(1-p)(n-k)

Når ganget sammen får vi:

Viktig informasjon:

• studier er uavhengige,
• Det er bare to mulige utfall i hver trial,
• sannsynligheten for «suksess» på hvert forsøk er konstant.,

Quincunx

Har en spille med den Quincunx (les deretter Quincunx Forklart) for å se den Binomiske Fordelingen i aksjon.

Kaste Terningen

En rettferdig terningen er kastet fire ganger. Beregne sannsynligheter for å bli:

• 0 Toere
• 1 To
• 2 Toere
• 3 Toere
• 4 Toere

I dette tilfellet n=4, p = P(To) = 1/6

X er en Tilfeldig Variabel ‘Antall Toere fra fire kaster’.,

Erstatning x = 0 til 4 i formel:

P(k av n) = n!k!(n-k)! pk(1-p)(n-k)

Som denne (til 4 desimaler):

Denne gangen grafen er ikke symmetrisk:

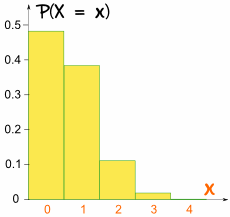
Det er ikke symmetrisk!

Det er skjeve fordi p er ikke 0.5

Sport Sykler

Din bedrift gjør sports sykler. 90% bestått avsluttende inspeksjon (og 10% mislykkes, og trenger å bli løst).

Hva er forventet Middelverdi og Varians av de 4 neste inspeksjoner?

Først, la oss beregne alle sannsynligheter.,

• for n = 4,
• p = P(Pass) = 0.9

X er en Tilfeldig Variabel «Antall omganger fra fire inspeksjoner».

Erstatning x = 0 til 4 i formel:

P(k av n) = n!k!(n-k)! pk(1-p)(n-k)

Middelverdi, Varians og Standardavvik

La oss beregne Gjennomsnitt, Varians og Standardavvik for Sports Sykkel inspeksjoner.

Det er (relativt) enkle formler for dem. De er litt vanskelig å bevise, men de gjør jobben!,

De mener, eller «forventet verdi», er:

μ = np

formelen for Variansen er:

Varians: σ2 = np(1-p)

Og standardavviket er kvadratroten av variansen:

σ = √(np(1-p))