Den Pytagoreisk Teorem

En av de mest kjente matematiske formler er Pytagoreisk Teorem, noe som gir oss forholdet mellom sidene i trekanten til høyre. En rett trekant består av to bein og en hypotenuse. De to bena møtes på en 90° vinkel og hypotenuse er den lengste siden i trekanten til høyre og motsatt side av høyre vinkel.,

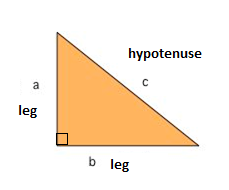
Pytagoreisk Teorem forteller oss at forholdet i hver rett trekanten er:

$$a^{2}+b^{2}=c^{2}$$

Eksempel

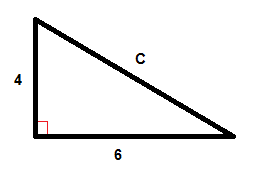
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\ca 7.2$$

Det er et par av spesielle typer høyre trekanter, som 45°-45° til høyre trekanter og 30°-60° høyre trekant.,

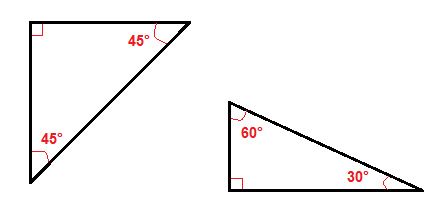
på Grunn av deres vinkler det er lettere å finne hypotenuse eller bena i disse høyre trekanter enn i alle andre høyre trekanter.

I en 45°-45° til høyre trekanten vi trenger bare å multiplisere ett ben ved √2 for å få den lengden av hypotenuse.

Eksempel

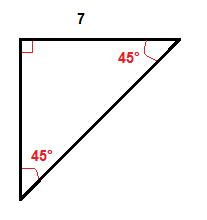
Vi multiplisere lengden på etappen, som er 7 tommer √2 for å få den lengden av hypotenuse.

$$7\cdot \sqrt{2}\ca 9.,9$$

I et 30°-60° høyre trekant kan vi finne lengden av foten som er på motsatt side av 30° vinkel ved hjelp av denne formelen:

$$a=\frac{1}{2}\cdot c$$

Eksempel

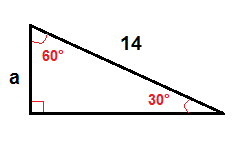
for Å finne en, vi bruker formelen ovenfor.

$$a=\frac{1}{2}\cdot 14$$

$$a=7$$

Video leksjon

Finne sider av denne retten trekant